20162330 2017-2018-1《程序设计与数据结构》第七周学习总结

2017-2018-1 学习总结目录：　1　2　3　5　6　7　9　10　11　12

栈、队列、链表都是线性数据结构，树是非线性结构（层次结构）。
非线性结构：（一对多）
除根结点之外的每个结点有且仅有一个直接前驱。
每个结点可以有多个直接后继。
除根结点之外，其他结点都存在唯一一条从根结点到该结点的路径。
树：结点 + 边（有限集合）
【注】结点数为0，称为空树。
结点类型：根结点（唯一）、子结点、父结点、兄弟结点（同父）、叶节点（无子结点）、内部结点（非根叶结点）。
结点的度：结点的子树数。
树的度：结点的最大度数。（如：二叉树的度为2）
叶子（叶结点）：度为0。
分支点：非终端结点。

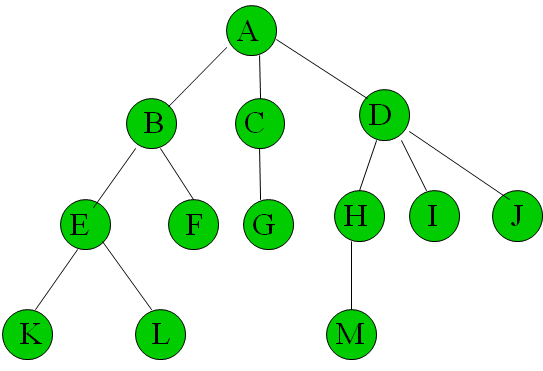
例如：上图中结点 K L F G M I J 的度为0，A D 结点的度为3，B E 结点的度为2，C H 结点的度为1，结点 A B C D E H 属于分支点。
结点的层次：根为第一层，以此类推。（从根到该结点的路径上的边数）
树的深度：结点的最大层次。
树的高度：从根到叶结点的最长路径的长度。
【注】深度不同于高度，还是以上图为例，该树的深度为4，高度为3。
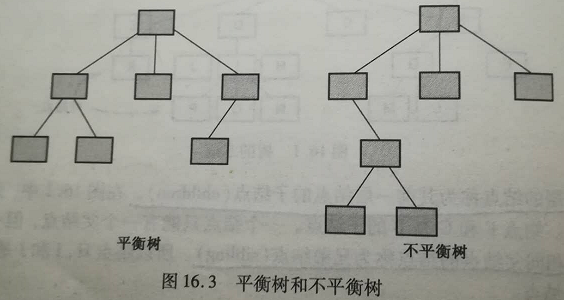
树的分类：n叉树（最大子结点数）、一般树（子结点无限制）、平衡树（子结点彼此不超出一层）、满树、完全树。

满树：所有叶结点在同一层，每个非叶结点都正好有n个子结点。
完全树：底层所有叶结点位于树的左侧，其余层结点全满。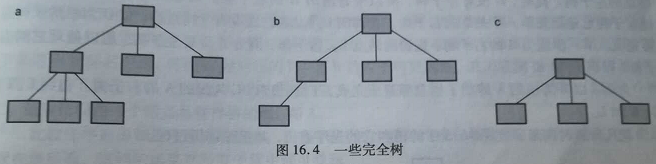

例如：上图中a和b是 非满完全树，只有c是 满完全树。
m个元素的平衡的n叉树的高度为log$_n$m，例如：有n个结点的平衡二叉树的高度为log$_2$n。（计算时取整加一）

树的遍历

先序遍历：访问根后，从左到右遍历子树。

中序遍历：遍历左子树，然后访问根，之后从左到右遍历余下子树。（把树压扁）

后序遍历：从左到右遍历各子树，最后访问根。

层序遍历：从上到下，从左到右遍历结点。

以二叉树的遍历为例：
先序遍历：若二叉树为空，则空操作；否则
(1) 访问根结点；
(2) 先序遍历左子树；
(3) 先序遍历右子树；

public void preorder(ArrayIterator<T> iter){
    iter.add(element);

    if(left != null)
        left.preorder(iter);

    if(right != null)
        right.preorder(iter);
}

中序遍历：若二叉树为空，则空操作；否则
(1) 中序遍历左子树；
(2) 访问根结点；
(3) 中序遍历右子树；

public void inorder(ArrayIterator<T> iter){
    if(left != null)
        left.inorder(iter);

    iter.add(element);

    if(right != null)
        right.inorder(iter);
}

后序遍历：若二叉树为空，则空操作；否则
(1) 后序遍历左子树；
(2) 后序遍历右子树；
(3) 访问根结点；

public void postorder(ArrayIterator<T> iter){
    if(left != null)
        left.postorder(iter);

    if(right != null)
        right.postorder(iter);

    iter.add(element);
}

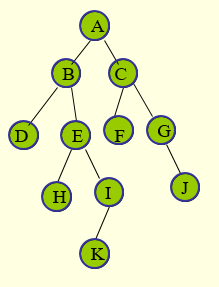
如上图所示，该树的不同遍历方式依次遍历结点的顺序如下：

先序遍历：A B D E H I K C F G J

中序遍历：D B H E K I A F C G J

后序遍历：D H K I E B F J G C A

层序遍历：（按层不按子树）

//树的根结点入队
//当队列不空时
{
	//结点出队列
	//访问结点
	//结点的左子结点入队
	//结点的右子结点入队
}

public Iterator<T> levelorder() {
    LinkedQueue<BTNode<T>> queue = new LinkedQueue<>();
    ArrayIterator<T> iter = new ArrayIterator<>();

    if(root != null){
        queue.enqueue(root);
        while(!queue.isEmpty()){
            BTNode<T> current = queue.dequeue();

            iter.add(current.getElement());

            if(current.getLeft() != null)
                queue.enqueue(current.getLeft());
            if(current.getRight() != null)
                queue.enqueue(current.getRight());
        }
    }
    return iter;
}

这三种遍历算法的访问路径是相同的，只是访问结点的时机不同。

已知某棵二叉树，容易求得它的某种遍历序列。但是，反过来，若已知某种遍历序列，是否可以唯一确定一棵二叉树呢？

重要结论：中序 + 先序，或 中序 + 后序 均能唯一确定一棵二叉树，但 先序 + 后序 却不一定能唯一确定一棵二叉树。

树的实现策略

使用数组表示树：存储在数组中位置为 n 的元素，元素的左子结点存储在（2n + 1）的位置，右子结点存储在（2 x（n+1））的位置。
链式结点：使用一个单独的类来定义树结点。

二叉树的实现

二叉树：树和子树的结点数最多有两个。
有序树：子树有左右之分。（左右不同会造成二叉树不同）
二叉树的 5 种不同形态如下图：
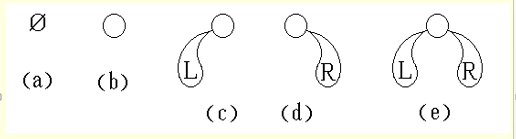
二叉树的重要性质：
若二叉树的根结点位于第1层，则：

性质1：在二叉树的第 i 层最多有 $2^{i-1}$ 个结点。（i ≥ 1）

性质2：深度为 k 的二叉树最多有 $2^k$-1 个结点。（k ≥ 1）

性质3：对任何一棵二叉树, 如果其叶结点个数为n$_0$, 度为2的结点数为 n$_2$, 则有：n$_0$＝n$_2$＋1。
特殊的二叉树：
满二叉树：每层充满结点，上文有解释。

深度为 k，层数为 i，根结点在第1层
结点总数 $2^k$-1
每层结点数 $2^{i-1}$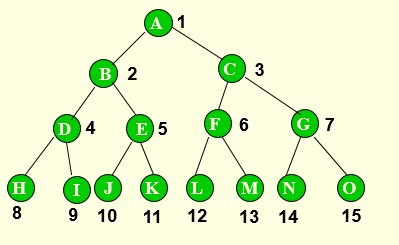

完全二叉树：满二叉树去掉右下方的结点，上文有解释。

树中所含的 n 个结点和满二叉树中编号为 1 至 n 的结点一一对应。
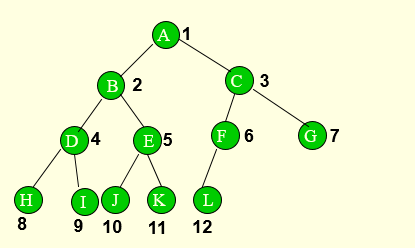
完全二叉树的性质：

性质1：具有n个结点的完全二叉树的高度为[log$_2$n]+1

性质2：如果将一棵有 n 个结点的完全二叉树自顶向下，同一层自左向右连续给结点编号1, 2, …, n，则对于任意结点 i (1 ≤ i ≤ n)，有：

若i = 1, 则该 i 结点是树根，它无双亲；

若2i >n , 则编号为 i 的结点无左孩子，否则它的左孩子是编号为 2*i 的结点；

若2i +1>n, 则编号为 i的结点无右孩子，否则其右孩子结点编号为 2*i+1；
二叉树的ADT及实现：（课本中已给出）

public interface BinaryTree<T> extends Iterable<T> {
    //  Returns the element stored in the root of the tree.
    public T getRootElement();

    //  Returns the left subtree of the root.
    public BinaryTree<T> getLeft();

    //  Returns the right subtree of the root.
    public BinaryTree<T> getRight();

    //  Returns true if the binary tree contains an element that matches the specified element.
    public boolean contains(T target);

    //  Returns a reference to the element in the tree matching the specified target.
    public T find(T target);

    //  Returns true if the binary tree contains no elements,and false otherwise.
    public boolean isEmpty();

    //  Returns the number of elements in this binary tree.
    public int size();

    //  Returns the string representation of the binary tree.
    public String toString();

    //  Returns a preorder traversal on the binary tree.
    public Iterator<T> preorder();

    //  Returns an inorder traversal on the binary tree.
    public Iterator<T> inorder();

    //  Returns a postorder traversal on the binary tree.
    public Iterator<T> postorder();

    //  Performs a level-order traversal on the binary tree.
    public Iterator<T> levelorder();
}

上文中提到过，可以使用链式存储实现二叉树，包括【结点类】和【方法类】

决策树

结点表示判定点，结点的孩子表示选择链。（设计专家系统）

【返回目录】

教材学习中的问题和解决过程

【问题1】：我看了书中第370页的定义：树的高度（height；或深度，depth）定义为树中从根到叶结点的最长路径的长度。图16.2中树的高度是3，因为从根到叶结点F（或G）的路径长度为3。我又看了老师的PPT，PPT中将A定义为第一层，这样就造成了该树的高度不等于深度，而书中的定义方式又说树的高度或深度，按照书中的意思理解，如果将A定义为第一层，则树的高度不等于深度，高度定义与路径长度有关，而路径长度为从根到该结点的路径上的边数。深度是指某结点的最大层次数。树的高度是否完全等同于深度？
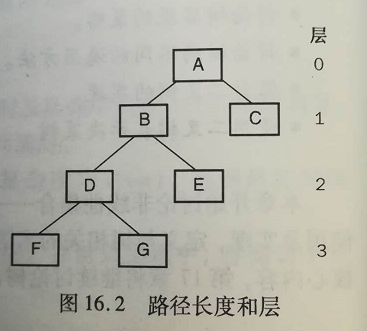
解决方案 ：（思考并查找资料）
对于这种问题，我有我的看法：对于没有将根结点定义为第0层的树来说，其高度不等于深度。查找到资料后验证我的猜想正确，一种解释为：

高度的定义为：从结点 x 向下到某个叶结点最长简单路径中边的条数。
【注意】对于是否是边的条数这个不清楚，待我后来查证，这个主要是由于其初值是1还是0来确定的，一般都是以1开始。

除此之外，我还得出了其他结论：

对于树中相同深度的每个结点来说，它们的高度不一定相同，这取决于每个结点下面的叶结点的深度。

另一种解释为：

引自考研大纲解析38页：树的深度是从根节点开始（其深度为1）自顶向下逐层累加的，而高度是从叶节点开始（其高度为1）自底向上逐层累加的。虽然树的深度和高度一样，但是具体到树的某个结点，其深度和高度是不一样的。我的理解是：非根非叶结点的深度是从根节点数到它的，高度是从叶节点数到它的。

这两种解释殊途同归，树的高度只有在根结点被定义为第0层时其高度才等同于深度。

【问题2】：课堂测试中的第一题：

有100个结点的完全二叉树，其高度是多少？叶结点数是多少？

第二问为什么答案是50个叶结点？
解决方案 ：（阅读课本）
我将课本和课件过了一遍，对于这样一个完全二叉树，首先其高度为[log$_2$100] + 1 = 7，将根结点定义为第一层，则在第六层一共有32个结点，前六层一共有63个结点，所以第七层有100 - 63 - 1 = 37个叶结点，所以上一层左侧一定会有19个内部结点，所以第六层就会有 32 - 19 = 13 个叶结点，所以一共有 37 + 13 = 50个叶结点。之前答错是因为没有动手大致画一遍，只是空想公式，理论又不扎实，错误率就会很高。

【返回目录】

代码调试中的问题和解决过程

【问题】：教材中的BTNode类和LinkedBinaryTree中的一些代码涉及到ArrayIterator类，无法调用该类，在API，源码中查找也没有该类。
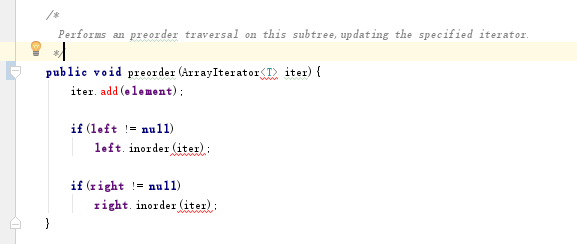
解决方案 ：（思考）
对于这个问题，我认为在查找不到的情况下有两种方案解决此问题：
一、自己写这个类，实现其调用的方法；
二、修改或者替换这个类。
我采用了第二种方法，通过查找一些资料，我了解到ArrayIterator类各不相同，确实是需要自己定义的，但是又觉得有些麻烦（懈怠了），所以打算替换此类，看到之后调用的add()方法，又看到原类的迭代对象是数组，所以我立刻想到了ArrayList类，正好该类又实现了Iterable接口。我的尝试暂时没有问题，只是还缺少一些测试来验证。

后来娄老师在上课时给出了自定义的ArrayIterator类，这个类继承了ArrayList类并实现了Iterator接口，加入后便可正常编译。

【返回目录】

代码托管

本周代码上传至 ch15 及 ch16 两个文件夹里：
（statistics.sh脚本的运行结果截图）

上周考试错题总结

【错题1】When one type of object contains a link to another object of the same type, the object is sometimes called __________ .
A .circular
B .recursive
C .self-referential
D .a stack
E .a queue
错误原因：书看得不细致，只凭自己的理解选了A。
加深理解：自指示关系的对象指的是同一类型的另一个对象。自指示关系组成了链表的基础，所谓链表就是一个链式结构，一个对象指向下一个对象，建立了表中对象之间的线性关系。
【错题2】It is possible to implement a stack and a queue in such a way that all operations take a constant amount of time.
A .true
B .false
错误原因：考虑到每个操作的时间复杂度都是O（1），因此需要很短的时间，错选B。
加深理解：一个理想的堆栈或者一个理想的队列实现的所有操作都需要大量持续时间。

【返回目录】

结对及互评

本周结对学习情况

本周莫礼钟状态有些下滑，不过还是抽出一定时间实现了使用链表实现队列的代码，掌握情况良好，除此之外还将课本上的十六章基础内容过了一遍，但是代码学习内容较少。本周也由于我的个人原因导致与莫礼钟的学习交流较少。在团队任务方面，莫礼钟在例会上主动承担采访有经验的学长或者老师这一项任务，虽然完成质量有待提高，但是对于团队的积极性值得表扬。
20162319
结对学习内容
- 使用链表实现队列（方法类）

其他（感悟、思考等，可选）

　　本周我的状态良好，比上周的效率高一些，本周我们学习了树结构，但是树的遍历方法仍然需要思考，包括上课时给出的一些重要结论和公式，这些都需要自己下去验证和熟悉。树结构在生活中的例子还是很多的，而且还有些激发我对我们团队游戏选取的兴趣。
　　本周的团队例会依然继续进行着，组建团队之后，我发现自己需要改进的地方还有很多，不仅仅是技术方面，在管理方面、计划方面都需要仔细考虑，通知类的消息还是落实到面对面交谈效果比较好，当然总体来说我们团队从一开始就非常出色，我觉得我们组只是按要求完成了老师的基础任务，并没有每项都做到完美，但是有时也能够得到老师的表扬，这可能是我们学院学风的根源问题吧。下周，我依然会和组长一起带领团队继续前进。

【附1】教材及考试题中涉及到的英语：

Chinese	English	Chinese	English
边	edge	自指示	self-referential
兄弟结点	sibling	祖先	ancestor
内部结点	internal node	先序遍历	preorder traversal
子树	subtree	中序遍历	inorder traversal
后继	descendant	后序遍历	postorder traversal
度	order	层序遍历	level-order traversal
遍历	traversal	模拟	simulation

【附2】本周小组博客

【返回目录】

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	234/234	1/28	14/14	了解算法效率、大O符号等理论内容
第二周	255/489	1/29	12/26	了解敏捷的团队、泛型的使用
第三周	436/925	2/31	10/36	了解一些查找和排序的算法
第四周	977/1902	3/34	10/46	掌握实现线性结构
第五周	800/2702	2/36	12/58	掌握实现栈集合
第六周	260/2962	1/37	8/64	掌握实现队列集合
第七周	843/3805	4/41	12/76	掌握实现树的基本结构

计划学习时间：14小时
实际学习时间：12小时
有效学习时间：5小时
改进情况：本周效率一般，主要感觉在团队日常管理上花费的时间较多，不过本周代码进度较好，会继续保持。

参考资料

【返回目录】

posted @ 2017-10-22 23:47 N-Liu 阅读(245) 评论(1) 编辑收藏举报

刷新页面返回顶部

(๑•̀ㅂ•́)و✧

20162330 2017-2018-1《程序设计与数据结构》第七周学习总结

目录

教材学习内容总结

树

树的遍历

树的实现策略

二叉树的实现

决策树

教材学习中的问题和解决过程

代码调试中的问题和解决过程

代码托管

上周考试错题总结

结对及互评

本周结对学习情况

其他（感悟、思考等，可选）

学习进度条

参考资料

公告