20162330 2017-2018-1《程序设计与数据结构》第三周学习总结
2017-2018-1 学习总结目录: 1 2 3 5 6 7 9 10 11 12
目录
- 0. 教材学习内容总结
- 0.1 查找
- 0.2 排序
- 0.3 分析查找与排序算法
- 1. 教材学习中的问题和解决过程
- 1.1 快速排序示例的理解
- 1.2 算法复杂度练习
- 2. 代码调试中的问题和解决过程
- 2.1 数组中的字符串元素排序
教材学习内容总结
1.查找
-
查找是在数据项中找到指定目标元素或是确定目标不存在的过程。
-
查找池中找到目标需要的比较次数会随着数据项的增加而增加;
查找算法作用于 Comparable (多态)对象中的数组(compareTo 方法比较元素)。 -
查找策略:
- ① 穷举法(线性查找)
- ② 分治(二分查找)
-
线性查找:依次比较,不要求有序,基于 Comparable 接口的实现,时间复杂度:O(n)
二分查找:效率高,适用于有序数据项,迭代,分治,时间复杂度:O(nlog\(_2\)n)
public static Comparable binarySearch (Comparable[] data, Comparable target){
Comparable result = null;
int first = 0, last = data.length - 1,mid; //查找范围
while(result == null && first <=last){
mid = (first + last)/2; //中间位置比较元素
if (data[mid].compareTo(target) == 0)
result = data[mid]; //查找成功
else
if(data[mid].compareTo(target) > 0)
last = mid - 1; //范围缩小到前半段
else
first = mid + 1; //范围缩小到后半段
}
return result;
}
【补充】二分查找算法主要步骤归纳如下:(假设是有序列表)
(1)定义初值:first = 0, last = length - 1;
(2)如果first ≤ last,循环执行以下步骤:
①mid = (first + last)/2;
② 如果 target 与 data[mid] 的关键字值相等,则查找成功,返回 mid 值,否则继续执行;
③ 如果 target 小于 data[mid] 的关键字值,那么last = mid - 1,否则first = mid + 1。
(3)如果first > last,查找失败,返回 null。
2.排序
-
排序:按照某种标准将一列数据项次序重排;
依据:关键字(字母、数字等);
顺序:递增、递减、非递增、非递减。 -
选择排序:扫描整个表,找到最小值,交换。反复将一个个具体的值放到它 最终 的有序位置。(整理无序扑克牌)
public static void selectionSort(Comparable[] data)
{
int min;
for(int index = 0 ; index < data.length - 1; index++) // 控制存储位置
{
min = index;
for(int scan = index + 1;scan < data.length; scan++) // 查找余下数据
if (data[scan].compareTo(data[min]) < 0) // 查找最小值
min = scan;
swap(data,min,index); // 交换赋值
}
}
交换方法:
private static void swap(Comparable[] data,int index1,int index2){
Comparable temp = data[index1]; //引入一个临时变量
data[index1] = data[index2];
data[index2] = temp;
}
-
示例:


-
插入排序:反复将一个个具体的值插入到有序的子序列中(合适位置)。(抓牌整理法)
伪代码及实现过程:
for(从第二个数据开始对所有数据循环处理)
{
while (第i个数据小于它之前的第i-1个数据)
{
将第i个数据复制到一个空闲空间临时存储,这个空间为“哨兵”
在前i-1个数据中寻找合适的位置,将从该位置开始的元素全部后移
将哨兵数据插入到合适位置
}
}
public static void insertionSort (Comparable[] data)
{
for (int index = 1; index < data.length; index++)
{
Comparable key = data[index];
int position = index;
// 哨兵临时存储
while (position > 0 && data[position-1].compareTo(key) > 0)
{
data[position] = data[position-1]; //位置全部后移
position--;
}
data[position] = key; //合适位置
}
}
-
示例:
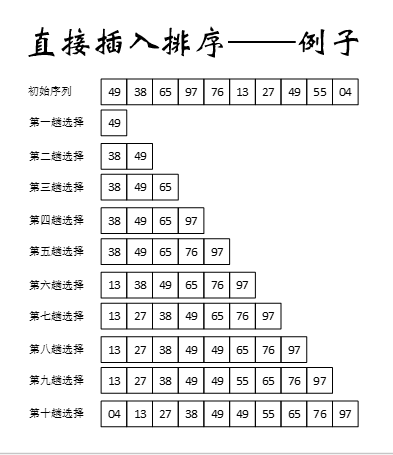
-
希尔排序:把一个长序列分割为若干个短序列,直接插入排序。
示例:
-
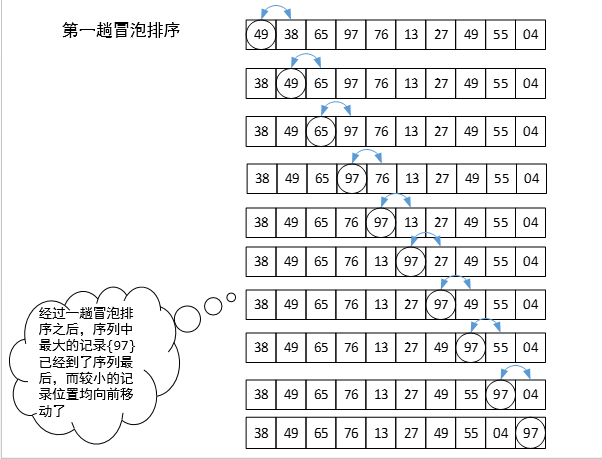
冒泡排序:反复比较相邻元素,如果必要就交换次序。
public static void bubbleSort (Comparable[] data)
{
int position, scan;
for (position = data.length - 1; position >= 0; position--)
{
for (scan = 0; scan <= position - 1; scan++)
if (data[scan].compareTo(data[scan+1]) > 0)
swap (data, scan, scan+1); //逆序交换
}
}
-
示例:

-
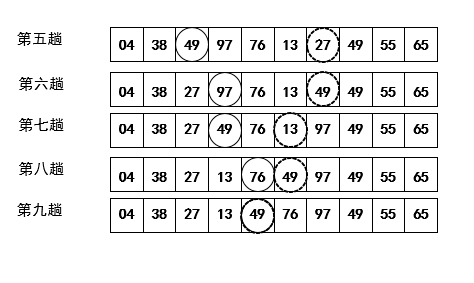
快速排序:根据枢轴划分序列,之后使用递归对子序列排序。
枢轴:一般而言我们选择整个序列的第一个数为枢轴。
public static void quickSort (Comparable[] data, int min, int max)
{
int pivot;
if (min < max)
{
pivot = partition (data, min, max); // make partitions(定义枢轴)
quickSort(data, min, pivot-1); // sort left partition
quickSort(data, pivot+1, max); // sort right partition
}
}
划分并排序:
private static int partition (Comparable[] data, int min, int max)
{
// Use first element as the partition value
Comparable partitionValue = data[min];
int left = min;
int right = max;
while (left < right)
{
// Search for an element that is > the partition element
while (data[left].compareTo(partitionValue) <= 0 && left < right)
left++;
// Search for an element that is < the partitionelement
while (data[right].compareTo(partitionValue) > 0)
right--;
if (left < right)
swap(data, left, right);
}
// Move the partition element to its final position
swap (data, min, right);
return right;
}
-
示例:


-
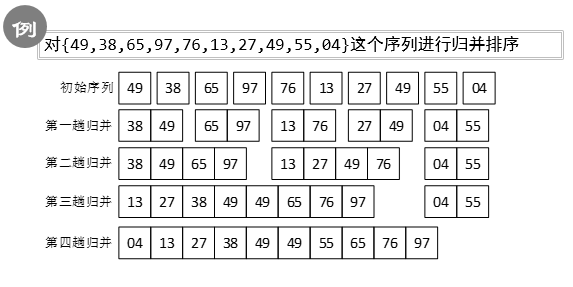
归并排序:递归平分,直到每个序列只含一个元素,之后归并为有序表。
public static void mergeSort (Comparable[] data, int min, int max)
{
if (min < max)
{
int mid = (min + max) / 2;
mergeSort (data, min, mid);
mergeSort (data, mid+1, max);
merge (data, min, mid, max);
}
}
归并算法中关键代码:
int first1 = first, last1 = mid; // endpoints of first subarray
int first2 = mid+1, last2 = last; // endpoints of second subarray
int index = first1; // next index open in temp array
// Copy smaller item from each subarray into temp until one
// of the subarrays is exhausted
while (first1 <= last1 && first2 <= last2)
{
if (data[first1].compareTo(data[first2]) < 0)
{
temp[index] = data[first1];
first1++;
}
else
{
temp[index] = data[first2];
first2++;
}
index++;
}
之后检查各个序列中的元素是否用尽,最后将有序数据复制回原数组。
-
示例:

-
分配排序:用额外空间节省时间。(桶排序、基数排序)
示例:

-
堆排序:堆积排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆性质:即子结点的键值或索引总是小于(或者大于)它的父结点。
示例:

3.分析查找及排序算法
-
考虑最差情形
-
查找算法:二分查找高效(对数阶)
-
排序算法:性能比较
排序方法 平均时间 最坏情况 辅助存储 冒泡排序 O(\(n^2\)) O(\(n^2\)) O(1) 选择排序 O(\(n^2\)) O(\(n^2\)) O(1) 希尔排序 O(nlogn) O(nlogn) O(1) 快速排序 O(nlogn) O(\(n^2\)) O(logn) 堆排序 O(nlogn) O(nlogn) O(1) 归并排序 O(nlogn) O(nlogn) O(n) 插入排序 O(\(n^2\)) O(\(n^2\)) O(1) 桶排序 O(n) O(\(n^2\)) O(n) 基数排序 O(d(n+k)) O(d(n+k)) O(d(kd)) 【注】表中n是排序元素个数,d个关键字,关键码的取值范围为k
教材学习中的问题和解决过程
-
【问题1】:在看本章内容的PPT时,快速排序有一个示例没看懂,只看图的话,我觉得实线圈中的数和加粗的虚线圈中的数的位置变动没有什么规律,所以不太理解快速排序的执行顺序。

-
解决方案 :在仔细阅读了相关内容之后,我发现实线圈中的数和加粗的虚线圈中的数的位置变动规律、比较顺序并不是受到同类线圈的影响,在选好枢轴以后,就开始首尾比较元素,以49为枢轴,左右依次比较,顺序就跳过一次,直到缩减到中间位置,便实现了划分序列。我原来是被不同的线圈中的数迷惑了,才弄错了执行次序。
【注】枢轴是一个数。 -
【问题2】:关于考试时的算法复杂度练习,求该算法的时间复杂度:
void fun3(int n)
{ int i=0,s=0;
while (s<=n)
{ i++;
s=s+i;
}
}
- 解决方案 :之所以做错是因为当时没有仔细考虑while循环的执行次数,利用数学中的等差数列公式,可以最后得到 \(\frac{T(n)*[T(n) + 1]}{2}\),可简化为\(T^2\)(n),而这个值又小于等于n,所以T(n) ≤ \(\sqrt{n}\),即时间复杂度为O(\(\sqrt{n}\))。
代码调试中的问题和解决过程
-
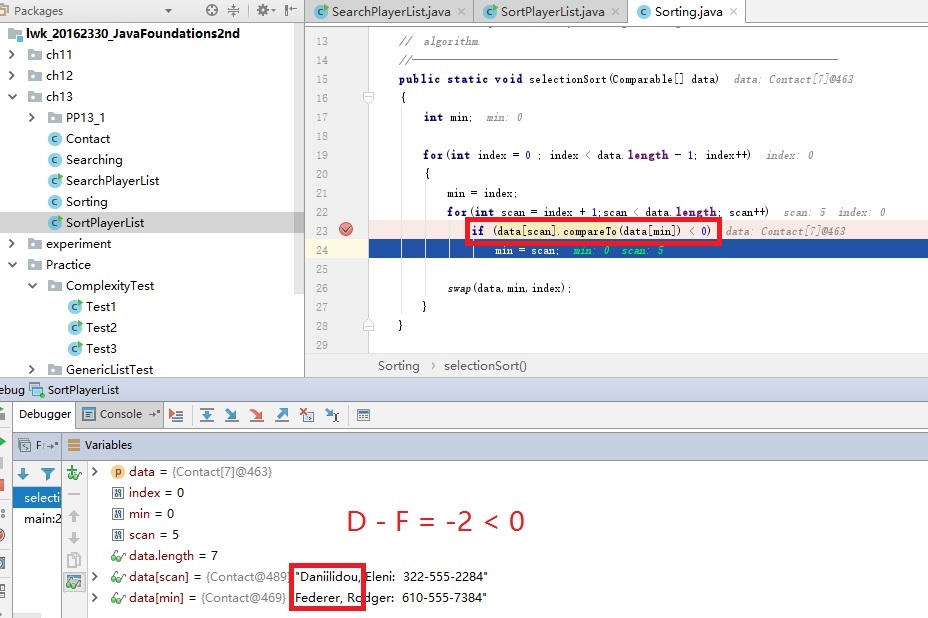
【问题】:在看教材代码程序13.4时,不理解将姓氏和名字交换过来之后怎么对数组中的字符串元素排序?

-
解决方案 :在IDEA中使用debug单步调试,我发现这里的关键字是按照字母的顺序排列,从而返回一个正整数,负整数或者0。如图所示:这里的scan索引是D开头的姓氏,而min索引是F开头的姓氏,使用compareTo比较时(ASCII码表中),相当于将字母当成数字相减,所以这里得出的是负整数-2,小于0,所以重新赋值,即最小索引对应的值。
代码托管
- 本周代码上传至 ch13 和 Practice 两个文件夹里:
(statistics.sh脚本的运行结果截图)

本周考试错题总结
-
本周课下测试还未给出错题和解析:

-
课上测试错题如下:
【错题1】有以下用Java语言描述的算法,说明其功能并计算复杂度
double fun(double y,double x,int n)
{
y=x;
while (n>1)
{
y=y*x;
n--;
}
return y;
}
【正解】计算\(x^n\);O(n)
【理解】当时因为循环前将x的值赋给了y,所以我有点纠结到底是计算\(x^n\)还是\(y^n\),最后写成\(y^n\)。仔细一想,在循环前的y是否赋值与循环内的x没有关系,即使循环之外y赋值为x,循环内仍然是x,如果将循环内的y理解为x那么y则是无规律增长的,所以这里是计算\(x^n\),至于O(n),我竟然忘记了加大O符号(¬_¬)。
- 【错题2】求该算法的时间复杂度:
void fun3(int n)
{ int i=0,s=0;
while (s<=n)
{ i++;
s=s+i;
}
}
【正解】O(\(\sqrt{n}\))
【理解】之所以做错是因为当时没有仔细考虑while循环的执行次数,利用数学中的等差数列公式,可以最后得到 \(\frac{T(n)*[T(n) + 1]}{2}\),可简化为\(T^2\)(n),而这个值又小于等于n,所以T(n) ≤ \(\sqrt{n}\),即时间复杂度为O(\(\sqrt{n}\))。
结对及互评
- 本周我的结对伙伴莫礼钟除了听了课堂上的一些内容之外,课后就没有其他学习活动了,我建议他把书过一遍,但是仍然被“狼人杀”束缚着,监督几次都没有效果。星期一的时候翻了几页构建之法,之后又忙于老乡会,保证过不再通宵玩游戏但是又通宵了一次。本学期只有第一周学习情况良好,之后便一蹶不振。
本周结对学习情况
- 20162319
- 结对学习内容
- 构建之法第十六章(一小部分)
其他(感悟、思考等,可选)
本周状态一般,比前两周稍差一些,有点匆忙,但是每当空闲时有有些缺少动力,本周课堂测试做得也不好,能做对的2分题没有得分,说明前一章的掌握情况有些死板。对于这周的学习内容,我明显感觉到难度在逐渐上升。这周的活动略多,总是突然来一个通知,有时会影响一天的计划,但是也不能因为事多就把主要精力大量分散。下周继续保持状态,求稳不求快。
-
【附1】教材及考试题中涉及到的英语:
Chinese English Chinese English 泛型 generic 划分元素 partition element 线性查找 linear search 枢轴点 pivot point 二分查找 binary search 优化 optimize 插入排序 insertion sort 子表 sublist(s) 归并排序 merge sort 子集 subset 排除 eliminate 指定的 designated -
【附2】本周小组博客:团队学习:《构建之法》
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 234/234 | 1/28 | 14/14 | 了解算法效率、大O符号等理论内容 |
| 第二周 | 255/489 | 1/29 | 12/26 | 了解敏捷的团队、泛型的使用 |
| 第三周 | 436/925 | 2/31 | 10/36 | 了解一些查找和排序的算法 |
-
计划学习时间:14小时
-
实际学习时间:10小时
-
有效学习时间:4小时
-
改进情况:学习时间有些下降,本周创建小组博客反复试验模板花费了一些不必要的时间,在代码上明显感觉有些乱,下周打算把课本上的内容再过一遍。

