20162330 2017-2018-1《程序设计与数据结构》第一周学习总结

2017-2018-1 学习总结目录：　1　2　3　5　6　7　9　10　11　12


目录


第12章 算法分析

教材学习内容总结

1.算法效率

  • 计算：信息处理的过程（借助某种工具）。

  • 计算模型 = 计算机 = 信息处理工具

  • 算法：特定计算模型下为解决问题所使用的指令序列（输入、输出、正确性、确定性、可行性、有穷性）。
    【注】好算法最重要的是效率，要求速度尽可能快，存储空间尽可能少。

  • 数据结构：指相互之间存在一种或多种特定关系的数据元素的集合。数据结构三要素为 逻辑结构、存储结构 和 运算 ，逻辑结构分为集合、线性、树、图，存储结构分为顺序、链式存储等，运算建立在前两个要素之上。

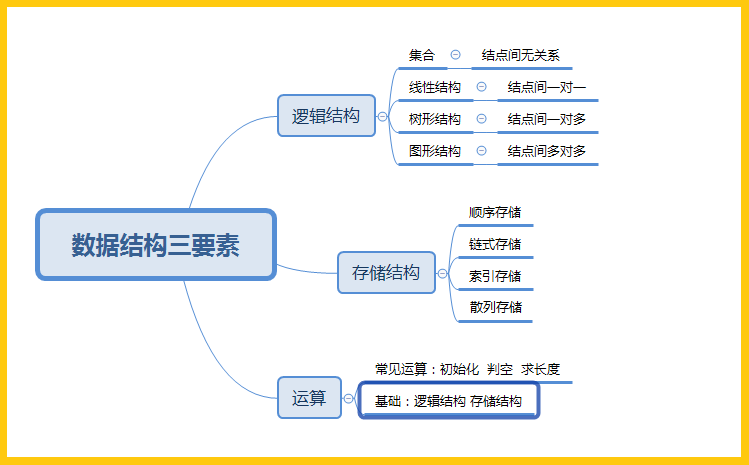
  • Algorithms + Data Structures = Programs （N.Wirth,1976）
    (Algorithms + Data Structures) x Efficiency = Computation

  • 算法效率的度量：算法效率主要由算法运行时间体现，算法运行时间等价于算法中每条语句执行时间之和，而每条语句执行时间又取决于每条语句的执行次数，所以可以把 语句频度 和 渐进时间复杂度 作为算法效率的度量单位。（RAM）

  • 算法效率的情形：最好效率、最差效率、平均效率。大量实践经验告诉我们，我们评价一个算法应该重点考虑 最差效率 这一点。举个例子：

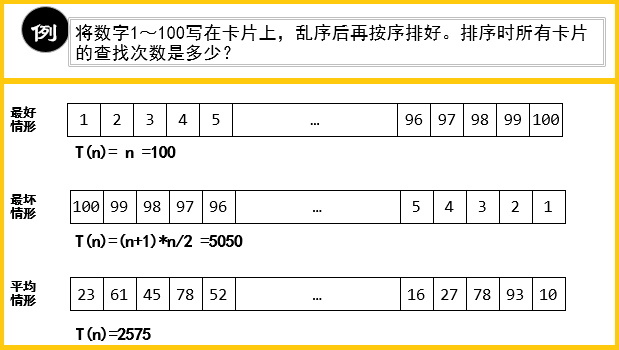
2.增长函数和大O符号

  • 增长函数：显示了与问题大小（n）相关的时间或空间利用率。

  • 语句频度：问题的规模为n时某个算法中的语句执行次数，记为 T(n)。

  • 时间复杂度：某个算法的语句执行次数 f(n) 的上限，即此算法的渐进时间复杂度（简称时间复杂度) 或执行时间，记为 O(f(n))。一个分析时间复杂度的例子：

    序号 程序语句 频度f(n)与规模n 时间复杂度O(f(n))
    1 x=x+1; y=x+2 f(n) = 2 O(1)
    2 for(i=0;i<n;i++) x++; f(n) = 2n+1 O(n)
    3 for(i=0;i<n;i++) for(j=0;j<n;j++) x++; f(n) = (n+1)+n*(n+1)+\(n^2\) O(\(n^2\))
    4 i=1; while(i<=n) i=i*2; \(2^{f(n)}\) = n O(log\(_2\)n)

  • 算法的阶：渐进复杂度称为算法的 阶 ，表示阶的记号称为 O（） 或 Big-Oh 。
    【注】算法的阶由算法增长的主项决定。一般情况下，阶相同的算法在效率上等价。

    渐进表示法记号 定义 含义
    O  f(n)＝O(g(n))，当 n ≥ n0 时，f(n) ≤ c·g(n)   f(n)的渐进上限为g(n) 
    Ω  f(n)＝Ω(g(n))，当 n ≥ n0 时，f(n) ≥ c·g(n)   f(n)的渐进下限为g(n) 
    Θ  f(n)＝Θ(g(n))，当 n ≥ n0 时，c\(_1\)·g(n) ≤ f(n) ≤ c\(_2\)·g(n)   f(n)的渐进确界为g(n) 

3.比较增长函数


  • 【注】c < log\(_2\)n < n < nlog\(_2\)n < \(n^2\) < \(n^3\) < 2n < 3n < n!
    处理器速度的提升不能弥补算法的低效率。

【返回目录】


教材学习中的问题和解决过程

  • 【问题1】我看了书中的第294页比较增长函数标题下的内容，对照图表，发现当问题大小为指数阶的A4时，速度提升了3.3（即原问题的大小加3），但是按照前3个算法的提升规律，当处理器速度提升10倍时的效果，算法A1改善了10倍，A2改善了根号10倍，A3改善了10的立方根倍，所以我觉得当时间复杂度是\(n^4\)时，提升倍数应该是10的四次方根，而书中表格内容直接加上了3.3，即 log$_2$10 ，而且书中的文字是指数阶复杂度，表格上A4算法就变成了幂阶时间复杂度，实在想不通。

  • 解决方案 ：询问王志强老师，之后得出正确结论：算法A4的时间复杂度应该为\(2^n\)，是中文版教材上有问题，这样一来就符合其速度提升的增长了。后来我也查询了英文版教材，发现在英文第三版教材中是正确的，此问题到此为止。

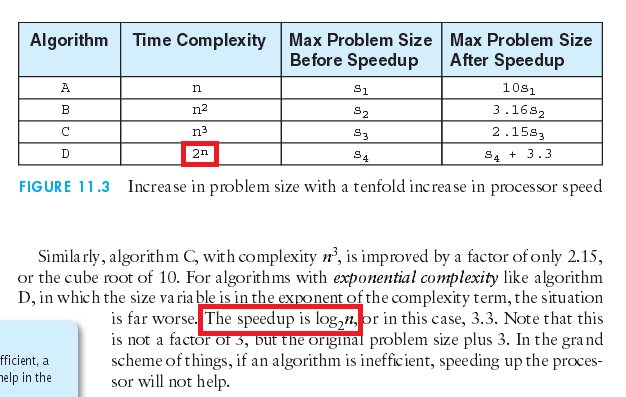
  • 【问题2】教材中提到“如果语句序列是线性的，则不管跳过什么样的语句，它的阶仍是O(n)”。不太理解什么是“线性”。之前学过“线性代数”，其中的“线性方程组”是指涉及数乘、加法的方程组，可是我依然不理解“线性”的含义。

  • 解决方案 ：查询之后了解到线性在这里可以简单地认为是一阶导数为常数的函数，“线性”就是指量与量之间按比例、成直线的关系。在Android开发中LinearLayout控件也有应用。

【返回目录】


代码调试中的问题和解决过程

  • 【问题1】：在根据程序语句分析频度 f(n) 时，想不通为什么第二层for的嵌套中频度为n(n+1)，我的理解是将n作为这层语句的频度，n+1作为上层语句的频度，但是上层能传入内层的频度只有n，紧接着，按这个思路分析，第三层的频度也无法理解。

  • 解决方案 ：询问王志强老师，之后发现我的思路从第二层开始就错了，第一层的n+1我能理解，但是我直接将第二层的n+1当成第一层传入的频度了，于是怎么都想不通。第一层传入的频度应该是n，而第二层在每次第一层传入时，都会增加n次频度，加上每次临界还要判断一次，所以一共是n*(n+1)次，第三层以此类推也能理解了，这也正是针对嵌套循环的乘法准则。原来我一直认为n+1是第一层的，现在看来还是当时被自己的思路绕晕了，换种思路便豁然开朗。

  • 【问题2】：在利用递归测试频度很高时的程序时，抛出异常StackOverflowError，我不太理解为什么相对其他简单算法，递归算法的容纳量（能够执行的次数）相对较少。

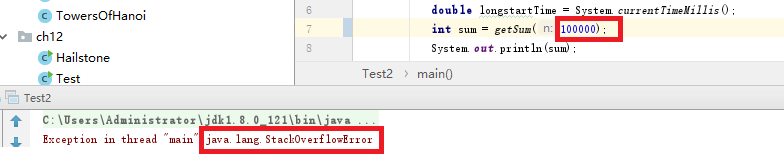
  • 解决方案 ：我原来只想要设计一个简单的递归来与其他算法比较，仅仅是一个累加相对于其他算法就少了那么多运算范围：

        public static int getSum(int n){
        if(n==1){
            return 1;
        }else{
            return n+getSum(n-1);
        }
    }

    查询了相关资料之后，我了解到一些理论解释：首先递归函数每次递归时都会调用一次本身的函数。函数调用的参数是通过栈空间来传递的，在调用过程中会占用线程的栈资源。而递归调用，只有走到最后的结束点后函数才能依次退出，而未到达最后的结束点之前，占用的栈空间一直没有释放，如果递归调用次数过多，就可能导致占用的栈资源超过线程的最大值，从而导致栈溢出，导致程序的异常退出。所以递归函数虽然较少代码量，但是会消耗大量资源，非必要的时候不要使用递归。这一点在我的假期博客中也有总结，当时的理解比较肤浅，现在终于验证了一次。

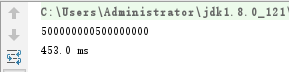
  • 顺便记录一下我对一个简单的问题使用不同算法的比较结果，我发现好的数学模型对于算法效率很重要，计算1到n的和的简单实例中，如果直接利用公式结论会比循环块很多，尤其对于项数较多的情况。虽然递归也比循环快，但是范围有限，资源有限，所以相比起来简洁的数学模型更胜一筹。以下是运行时间的简单测试：
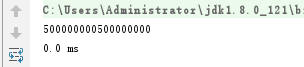
    循环与递归的比较：（上：循环；下：递归）


    循环与数学公式的比较：（上：循环；下：公式）

【返回目录】


代码托管

  • 本周代码上传至ch11和ch12两个文件夹里：

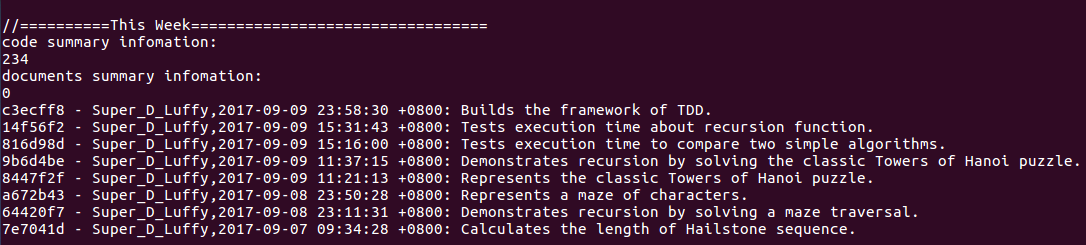
    （statistics.sh脚本的运行结果截图）

本周考试错题总结

  • 【错题1】Determine the order of the following pseudocode fragment.
for j = 1 to n
 if (a > b) then
  for i = 1 to n
   print i
  next i
 else
  for i = 1 to 10
    print i
  next i
 end if
next j

A .O(1)
B .O(log n)
C .O(n)
D .O(n2)
E .O(2n)
F .None of the above

  • 错误原因：没有考虑到时间复杂度的情形，错选C。
    加深理解：这段代码片段最差的时间复杂度是O(n2)。在最好的情况下，它是O(n)。在不了解a和b的情况下，不可能找到平均情况的时间复杂度，除非另有说明，算法的阶是指它最差的时间复杂度。所以我们评价一个算法也应该重点考虑 最差时间复杂度 这一点。

  • 【错题2】Determine the order of the following pseudocode fragment.

for i = 1 to 2*n
 print i
 print a
 print n
next i

A .O(1)
B .O(log n)
C .O(n)
D .O(n2)
E .O(2n)
F .None of the above

  • 错误原因：对算法的阶理解有误，认为这个循环执行了2n次阶就是2n，错选E。
    加深理解：这个循环将被执行2n次。但是当用大O符号表示算法的阶时，常量就被忽略了。

  • 【错题3】Suppose Computer Program A implements an algorithm of order O(n). Suppose Computer Program B implements an algorithm of order O(n2). If the programs begin execution at the same time, we know that Computer Program A will complete execution first.
    A .true
    B .false

  • 错误原因：没有考虑一些客观因素（输入、频度等），错选A。
    加深理解：虽然计算机程序A被认为是“更快的”，但是我们不知道哪个程序会先完成，因为我们不知道输入的大小或者与两个算法的运行时间相关联的常量。

【返回目录】


结对及互评

  • 莫礼钟是我新的结对伙伴，他在学习上不是很主动，需要督促，我会适度监督他，尽可能让他恢复一些学习的动力。本周他的状态比上学期好一些，看了云班课的几个视频也做了笔记，希望他可以继续保持。

本周结对学习情况

  • 20162319
  • 结对学习内容
    • 云班课上的视频
    • 图灵机模型

其他（感悟、思考等，可选）

  • 本周是开学的第一周，我的状态良好，较稳定，本周主要以理论内容为主，代码实践内容较少，我针对简单的累加做了不同算法的测试。对照着课本，也看了云班课上的视频，虽然有些迷茫，但是本周的大体内容已掌握，可以说本周的学习任务相对较少。我觉得娄老师在课堂上讲得有些快，所以课下也用了一些时间消化。下周会继续保持(•̀ᴗ•́)و

  • 【附】教材及考试题中涉及到的英语：

    Chinese English Chinese English
    增长函数 growth function 伪代码 pseudocode
    时间复杂度 time complexity （代码）段 fragment
    空间复杂度 space complexity 记号 notation
    渐进复杂度 asymptotic complexity 算法 algorithm
    主项 dominant term 十倍（的） tenfold
    （算法的）阶 order 实现（执行） implement
    常量 constant 子句 clause
    数量级 order(s) of magnitude 插图 illustration

【返回目录】


学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 234/234 1/28 14/14 了解算法效率、大O符号等理论内容

  • 计划学习时间：15小时

  • 实际学习时间：14小时

  • 有效学习时间：5小时

  • 改进情况：第一周效率相对较高，要保持好状态，提高课堂效率。还是那句话：保持较低的动力，每天进步一点点。


参考资料

【返回目录】

posted @ 2017-09-10 17:47  N-Liu  阅读(429)  评论(3)  编辑  收藏  举报