由遍历序列构造二叉树

实验3：由遍历序列构造二叉树

二叉树构造定理：

  • 定理7.1：任何n（n>0）个不同结点的二又树，都可由它的中序序列和先序序列唯一地确定。
  • 定理7.2：任何n（n＞0）个不同结点的二又树，都可由它的中序序列和后序序列唯一地确定。

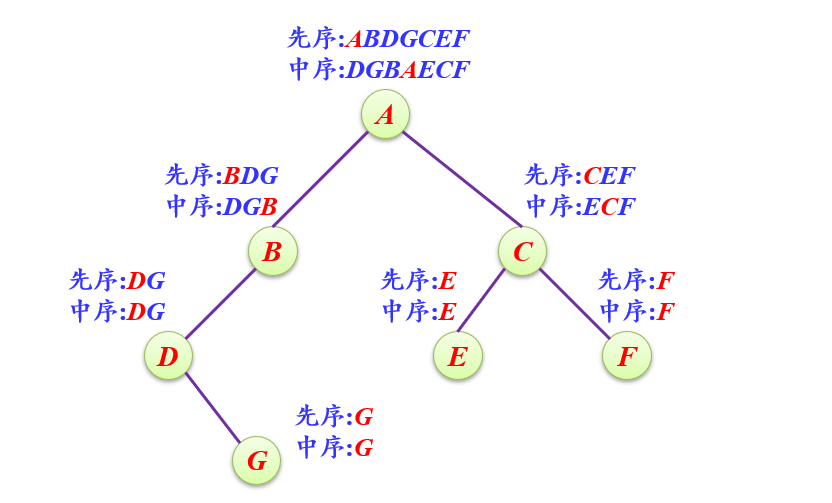
题目： 已知先序序列为ABDGCEF，中序序列为DGBAECF，则构造二叉树的过程如下所示。

 

 C语言代码示例：

 1 #include<stdio.h>
 2 #include<malloc.h>
 3  
 4 typedef struct node
 5 {
 6     struct node *lchild, *rchild;
 7     char data;
 8 } BTNode;
 9  
10 BTNode* CreateBTree(char *pre, char *in, int n)
11 {
12     int k;
13     char *p;
14     if (n <= 0)
15         return NULL;
16     BTNode *b = (BTNode*)malloc(sizeof(BTNode));
17     b->data = *pre;
18     for (p = in; p < in + n; ++p)
19         if (*p == *pre)
20             break;
21     k = p-in;
22     b->lchild = CreateBTree(pre+1, in, k);
23     b->rchild = CreateBTree(pre+k+1, p+1, n-k-1);
24     return b;
25 }
26  
27 void dispBTree(BTNode *b) 
28 {
29     if(b!= NULL)
30     {
31         printf("%c", b->data);
32         if(b->lchild != NULL || b->rchild != NULL)
33         {
34             printf("(");
35             dispBTree(b->lchild); 
36             if(b->rchild != NULL)
37               printf(",");
38             dispBTree(b->rchild);
39             printf(")");                 
40         }
41     }
42  } 
43  
44 int main()
45 {
46     BTNode* b;
47     char pre[] = "ABDGCEF";
48     char in[] = "DGBAECF";
49     int n = 7;
50     b = CreateBTree(pre, in, 7);
51     dispBTree(b);
52     return 0; 
53 }
View Code

 运行结果：

 

 

C++代码示例：

 1 /**
 2  * Definition for a binary tree node.
 3  * struct TreeNode {
 4  *     int val;
 5  *     TreeNode *left;
 6  *     TreeNode *right;
 7  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 8  * };
 9  */
10 class Solution {
11 public:
12     TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
13     {
14       TreeNode *b = CreateBTree(preorder.begin(), inorder.begin(), inorder.size());
15         return b;    
16     }
17     
18     TreeNode* CreateBTree(vector<int>::iterator p, vector<int>::iterator q, int n)
19     {
20         TreeNode *b;
21         auto s = q;
22         int k;
23         if(n <= 0)
24             return nullptr;
25         b = new TreeNode(*p);
26         for(; s < q + n; ++s)
27             if(*s == *p)
28                 break;
29         k = s - q;
30         b->left = CreateBTree(p+1, q, k);
31         b->right = CreateBTree(p+k+1, s+1, n-k-1);
32         return b;
33     }
34 };
View Code

 

posted @ 2018-09-19 16:32  苏格拉底的落泪  阅读(1893)  评论(0)  编辑  收藏  举报