python 算法 day4

复杂递归问题——河内塔问题

河内塔问题是法国数学家爱德华·卢卡斯于1883年发现的。他受到一个关于印度教寺庙的传说的启发,故事中这一问题交由年轻僧侣们解决。最开始,僧侣们得到三根杆子,64个金圆盘堆叠在其中一根上, 每个圆盘比其下的小一点。僧侣们的任务是将64个圆盘从一根杆上转移到另一根杆上,但有两项重要的限制,一是他们一次只能移动一个圆盘,一是不能将大圆盘放在小圆盘之上。僧侣们日以继夜地工作,每秒移动一个圆盘。 传说中,当工作完成之时寺庙就会崩塌, 世界则将不复存在。

 

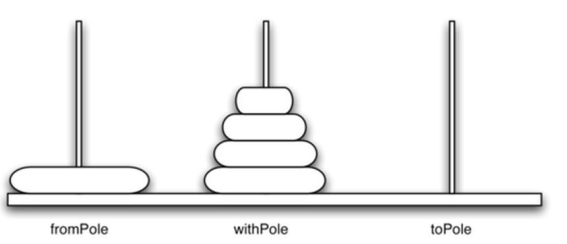
 假设你有一个五个圆盘组成的塔,最开始在一号杆上。如果你已经知道如何将有四个圆盘的小塔从一号杆移到二号杆,就可以很容易地将第五个圆盘移动到三号杆,然后将四个圆盘的塔从二号杆移动到三号杆。但是如果你不知道如何移动有四个圆盘的塔呢?这时又假设你知道如何将有三个圆盘的塔移到三号杆;然后你就可以将第四个圆盘移动到二号杆,然后再将位于三号杆的有三个圆盘的塔移到其上。但是如果你不知道如何移动有三个圆盘的小塔又怎么办呢?那考虑先将有两个圆盘的小塔移动到二号杆,再将第三个圆盘移动到三号杆,最后将两个圆盘的小塔移动到三号杆会如何呢?但如果你连这个也不会,该如何处理?显然你知道将单个圆盘移到三号杆十分简单甚至可以说无需思考,似乎这就是这一问题最基础的部分。

抽象概述：

1、把圆盘数减一层数的小塔经过目标杆移动到中间杆

2、把剩下的圆盘移动到目标杆

3、把圆盘数减一层数的小塔从中间杆，经过起始杆移动到目标杆

def moveTower(height,fromPole,toPole,withPole):
    if height >= 1:
        moveTower(height-1,fromPole,withPole,toPole)#我们把除了最下面的圆盘全部移动到中间杆
        moveDisk(fromPole,toPole)  #将原来在最底层的最大圆盘移动到目标杆
        moveTower(height-1,withPole,toPole,fromPole)#将中间杆的圆盘移动到最大圆盘的上面


def moveDisk(fp, tp):
    print("moving disk from ",fp,"to",tp)

moveTower(4,"A","B","C")