SQL2008空间数据类型--欧氏几何2类与方法

2  类与方法

在上一篇博客中说道了几何数据类型（点、线、面和集合）的定义，既然几何数据类型是通过CLR来扩展出来的，学习过C#的都知道，一个对象下面会有属性和方法，那么几何数据类型对应的也有其属性和方法。下图就能够反映出这些几何对象的类关系。

由于我自己本身对C#比较熟悉（其实其他语言也就不怎么会了），这里我就按照C#的方式来讲一下。

首先要将的是函数。函数分为几种：构造函数、静态函数和实例下的函数。

2.1先说构造函数：

构造geometry对象及其下面的子对象有多种构造函数：通过熟知文本WKT构造、通过熟知二进制WKB构造和通过GML构造。如下语句就是通过WKT构造一个geometry对象。

DECLARE @g geometry;
SET @g = geometry::STGeomFromText('POINT (1 2)', 0);

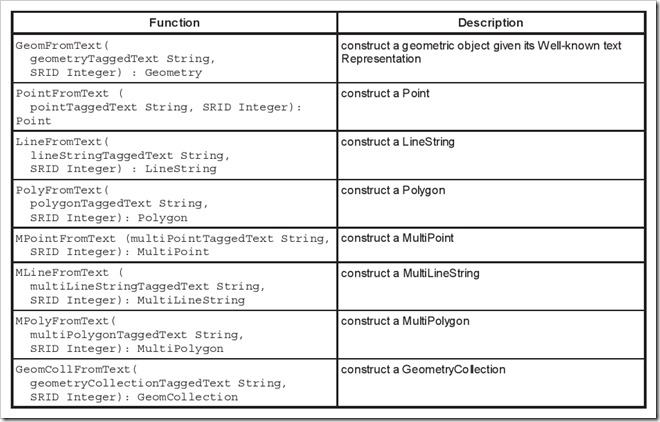
除了构造geometry对象外，每个子类也有自己的构造函数，下表给出了每个类的通过WKT构造的函数，通过WKB构造的函数类似，这里就不给出了。

该表取自OGC官方文档，在SQL2008中使用时函数名前面有ST前缀。比如同样构造一个点1，2 对应是SQL为：

SET @g = geometry::STPointFromText('PoINT (1 2)',0);

构造函数必须与给出的WKT类型对应，这里完全可以认为是C#中做的一个类型转换，如果类型不对应强制转换必然失败，比如：

SET @g = geometry::STLineFromText('PoINT (1 2)',0);--错误的代码

2.2通过构造函数实例化了一个对象后，接下来我们就要调用这个对象的方法了。

由于Geometry类是其他类的父类，所以先说该类的实例方法，这些方法将在其继承的类中同样适用。

• STAsText 返回实例的WKT表示形式
• ToString 返回实例的WKT表示形式
• STAsTextZM 返回实例的WKT表示形式 ，包括Z和M值
• STAsBinary 返回实例的WKB表示形式
• STAsGml 返回实例的GML表示形式
• STGeometryType 返回几何图形的实例类型,字符串，如LineString、Polygon等 ，相当于C#中的GetType().ToString()方法
• InstanceOf 确定几何图形是否为给定的实例类型，其实就相当于C#中的is关键字。比如SELECT @g.InstanceOf('GEOMETRYCOLLECTION');
• STIsValid 确定几何图形实例对其实例类型而言格式是否正确，有些申明虽然符合语法但是不符合OGC规定，所以需要用这个来校验。比如SET @g = geometry::STGeomFromText('LINESTRING(0 2, 1 1, 1 0, 1 1, 2 2)', 0);就是校验会失败的定义。
• MakeValid 将几何图形实例转换成具有实例类型的格式正确的几何图形实例，比如上面提到的校验失败的实例就可以使用SET @g=@g.MakeValid();这样系统会将实例转换为MULTILINESTRING ((0 2, 1 1, 2 2), (1 1, 1 0))
• STDimension 返回实例的最大维度，点是0维，线是1维，面是2维，如果是集合就要看几何中最大的纬度了。比如SELECT @g.STDimension();
• STSrid是属性，返回实例的SRID值。如：SELECT @g.STSrid
• STIsEmpty确定实例是否为空，如果为空则返回1，否则返回0。注意这里的空并不是NULL的意思哈。比如SET @g = geometry::STGeomFromText('POLYGON EMPTY', 0); SELECT @g.STIsEmpty();
• STIsSimple确定实例是否是简单的。所谓简单就是指满足：1.实例的每个图形不能与自身相交，但其终点除外。2.实例的任何两个图形不可在某个点上相交，但两个边界上的点除外。如图左边LineString(1 0,1 2,2 1,0 1)自身相交不是简单的，右边MultiLineString((0 0,0 2,2 2,2 0),(3 0,1 1))两个图形相交也不是简单的。

• STBoundary 返回实例的边界。这里的边界是：1.点和点集合没有边界，返回空几何图形；2.线和线集合边界由起始点和终点形成，并删除那些出现次数为偶数的点，返回MultiPoint类型；3.面和面集合的边界是其环的集合，返回MultiLineString类型。
• STEnvelope 返回实例的包络线。包络线是一个由实例的最小和最大坐标 (X,Y) 形成的轴对齐矩形，返回一个Polygon类型。对于线和面都好确定最大最小坐标，那么点怎么确定啊？点的包络线实际上就是一个无限小的矩形，比如Point(1 1)的包络线就是POLYGON ((0.999999 0.999999, 1.000001 0.999999, 1.000001 1.000001, 0.999999 1.000001, 0.999999 0.999999))

以上说的就是geometry的方法，接下来说一下子类的方法。

Point类的方法：

• STX是Point类的属性，返回点实例的 X 坐标。使用如：SELECT @g.STX;
• STY是Point类的属性，返回点实例的 Y 坐标。使用如：SELECT @g.STY;

Curve类的方法:

• STStartPoint 返回实例的起始点，也就是定义的第一个点，返回Point类型。
• STEndpoint 返回实例的终点，也就是定义的最后一个点，返回Point类型。
• STIsClosed 确定实例是否闭合，也就是起点和终点相同。返回bit类型。
• STIsRing 确定实例是否为环，所谓环就是要求既是简单的又是闭合的Curve。返回bit类型
• STLength 返回实例的长度，返回float类型。

LineString类的方法：

• STNumPoints 返回构成实例的点数。也就是申明LineString时的点的个数，重复的点要重复计数。
• STPointN 返回实例中的特定点。显然，@g.STStartPoint() 就是@g.STPointN (1)，而@g.STEndpoint() 就是@g.STPointN (@g.STNumPoints ())

Surface类的方法：

• STCentroid 返回多边形实例的几何中心点。也就是返回其重心的坐标，Point类型。
• STPointOnSurface 返回位于实例上的某个任意点，返回Point类型。这里说的是任意点，但是对于一个图形好像返回的总是同一个点，并不是随机的，只能说返回的点是在图形内，但是具体怎么算的我就不知道了。
• STArea 返回实例的面积，这个就不用多说了吧，如果中间带孔是要扣除孔的面积的。返回float类型。

PolyGon类的方法：

• STExteriorRing 返回多边形实例的外环。也就是STBoundary 方法再去掉中间的孔的边界。返回LineString。
• STNumInteriorRing 返回多边形的内环数。也就是孔的数量。返回int。
• STInteriorRingN 返回多边形的指定内环。也就是找到其中的一个孔的环，返回的是LineString类型。

GemoColllection类的方法：

• STNumGeometries 返回几何图形集合实例中的几何图形数目，如果是Point等非集合的实例，则返回1，空实例返回0.使用如：SELECT @g.STNumGeometries();相当于C#中一个数组的Length属性或集合的Count属性。
• STGeometryN 返回几何图形集合实例中的特定几何图形实例，传入参数n表示要取第几个图形，从1开始计数。对于Point等非集合对象传入1则返回本身。使用如：SELECT @g.STGeometryN(1)。相当于C#中的[n]

MultiCurve类的方法：

• STIsClosed 确定实例是否闭合，也就是起点和终点相同。返回bit类型，必须集合中的所有Curve都Close了才返回1，否则返回0。
• STLength 返回实例中所有Curve的长度的总和，返回float类型。

MultiSurface类的方法：

• STCentroid 返回多边形集合的重心的坐标，Point类型。
• STPointOnSurface 返回位于集合某实例上的某个任意点，返回Point类型。
• STArea 返回集合中所有多边形的面积的总和，返回float类型。

这里就把每个类和类下面的方法介绍完了，下一次就讲讲两个对象之间的关系和操作了。