算法学习——递归之汉诺塔
本文为作者原创,允许转载,不过请在文章开头明显处注明链接和出处!!! 谢谢配合~
作者:stars-one
链接:https://www.cnblogs.com/stars-one/p/9865560.html
本篇大约有834个字,阅读预计需要1.04分钟
算法描述
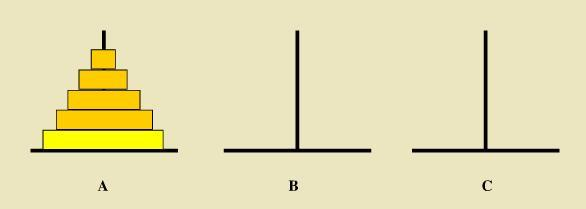
汉诺塔问题
如下图所示,从左到右有A、B、C三根柱子,其中A柱子上面有从小叠到大的n个圆盘,现要求将A柱子上的圆盘移到C柱子上去,期间只有一个原则:一次只能移到一个盘子且大盘子不能在小盘子上面,求移动的步骤和移动的次数
算法思路
-
1个盘的时候,只需要移动1次即可达成目标,
g(1) = 1)(步骤一) -
2个盘的时候,需要移动3次即可达成目标,
g(2) = 3(步骤二) -
3个盘的时候,我们需要将底下较大的两个盘先移动到C中,之后再将A中剩下的那个盘移动到C中。
这里需要注意的是,我们是将底下的2个盘当做了一个,所以是相当于进行了2次步骤二
需要2*g(2)次之后就是步骤一的那种情况 ,
需要1次移动g(3)=2*g(2)+1通式为
g(n)=2*g(n-1)+1递归出口为
n=1
算法实现
System.out.println("请输入盘片数:");
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
scanner.close();
long result = han(n);
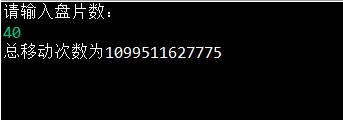
System.out.println("总移动次数为"+result);
}
public static long han(int n){
long s;
if(n==1){
s=1;
}else{
s =2*han(n-1)+1;
}
return s;
}
结果






【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】博客园携手 AI 驱动开发工具商 Chat2DB 推出联合终身会员
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 为什么 .NET8线程池 容易引发线程饥饿
· golang自带的死锁检测并非银弹
· 如何做好软件架构师
· 记录一次线上服务OOM排查
· Linux实时系统Xenomai宕机问题的深度定位过程
· 2025年广告第一单,试试这款永久免费的开源BI工具
· o3 发布了,摔碎了码农的饭碗
· SQL优化的这15招,真香!
· [.NET] API网关选择:YARP还是Ocelot?
· 将 EasySQLite 从 .NET 8 升级到 .NET 9