凹凸贴图与法线贴图
一般的纹理映射虽然可以添加精致的表面细节,但它无法影响物体表面的光照细节,因此不适合模拟粗糙表面。生成物体凹凸表面的一个简单的方法是对其表面法向量添加扰动,影响光照效果,这种技术又称凹凸映射(bump mapping)。同一般的纹理映射一样,凹凸映射也需要一张纹理图,但这张图通常是灰度图,存放的也仅仅是像素的高度信息。实际产生效果的时候是通过计算凹凸图中相邻像素的高度差值来改变表面法向量的值。如下图: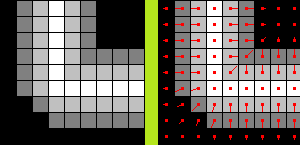
左边是凹凸图的一部分,右图则显示出各像素点间的高度差值(用向量表示),这个向量有很多种计算方式,不同的方法精确度不同,但是选择什么方法要取决于你所要求的精确度是个什么层次。最通常的方法是分别计算每个点上X和Y的倾斜度:
x_gradient = pixel(x-1, y) - pixel(x+1, y)
y_gradient = pixel(x, y-1) - pixel(x, y+1)
为了能用这两个斜度值对法线进行正确的干扰,我们必须在物体表面定义一个局部坐标系。
将每个顶点看成坐标原点,然后分别使用该顶点的切线T (Tangent),第二法线B (Binormal)和法线N (Normal)构成一个坐标系。在几何上,由T B N组成的坐标系称为Frenet Frame。于是这个贴图坐标系F就可以表示为:
F = [ T B N ]
只要知道F其中任意两个分量,都可以求出第三个分量,它们之间有这样的关系:
T = B × N
B = N × T
N = T × B
实际上可以这样理解,副法线B对应的是纹理空间坐标系的u轴,而切向量T对应了纹理空间的v轴,于是很容易得到干扰后的法向量:
New_Normal = Normal + (B * x_gradient) + (T * y_gradient)。
看到这里,我们可能会想,为什么不直接把法线信息存在纹理中,在需要的时候直接取出来用呢?这种想法正是法线贴图的想法,实际上法线贴图也可以算是一种特定的凹凸贴图方法。DX中有专门的函数D3DXComputeNormalMap可以从一张高度图生成法线图,法线图的RGB分别是原高度图该点的法线指向:Nx、Ny、Nz。法线图一般看起来比较怪异(通常偏紫色),如下图:

虽然从法线图可以直接得到法线向量(注:要通过一定的转换,把颜色值从0x00-0xff范围转到-1~1范围(因为0x00-0xff要表示正负两个方向的向量值,所以[0x80,0x80,0x80]才表示向量为零向量),并规范化),但是我们仍然需要用到切向空间的信息,就是说我们需要副法线向量B和切线向量T的值,这样才能将法线图中的信息转换到局部坐标系下,否则同一个物体变换一下方向,我们就得需要更新一下法线图,不可重用,而动画就更没办法使用了。对于顶点切线T和副法线B,我们只需要求出一个,就可以用公式T = B × N和B = N × T得到另一个,DirectX中提供了专门的求顶点切线的API,但我们也可以通过参考文章[1]中给出的方法来求切线。精确到表面每一个像素的切线T的计算可以用与普通纹理贴图一样的插值算法(如双线性插值)来得到,最后将从法线图中得到的法线inputnormal转化到物体表面的局部坐标空间下:
finalnormal = inputnormal.b * B + inputnormal.g * T + inputnormal.r * N
下图是我在之前的pathtracing算法中加入了法线贴图后的效果,感觉还行。
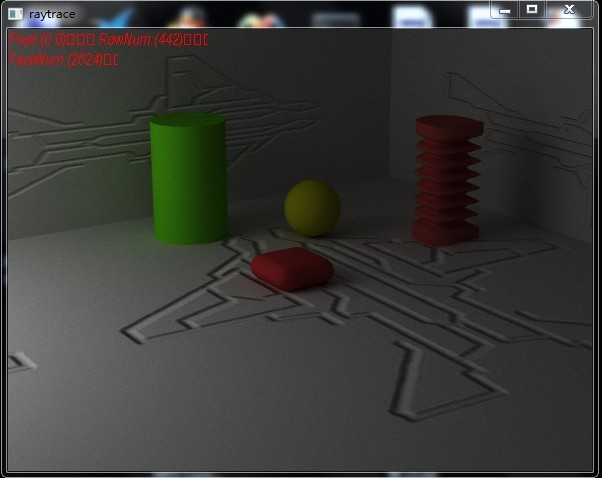
最后需要说的是不管是凹凸贴图还是法线贴图都只是一种障眼法,仔细看还是能看出不真实的地方,如模型无法产生自阴影,当光照方向与表面法线方向角度很大时,无法看到由于凸起部分的遮挡而产生的阴影。并且,也无法在物体边缘看到凹凸现象,因为它本身不会改变模型。可以看出下面的球体虽然使用了凹凸贴图,但是球的边缘仍然保持圆形而并没有显示出起伏。当下用曲面细分的方法可以产生真实的多边形细节来模拟物体表面的凹凸不平,随着技术的不断进步,可能某一天凹凸贴图就会被曲面细分方法或者其他技术替代。

参考文章:
[1].Computing Tangent Space Basis Vectors for an Arbitrary Mesh
http://www.terathon.com/code/tangent.html
[2].凹凸贴图(Bump Map)实现原理以及与法线贴图(Normal Map)的区别
http://hi.baidu.com/niujingqian/item/c5e897130a4aac031994ecda
[3].openGL CG 系列教程06 – Normal Mapping (法线贴图)



