读书笔记：《思考的乐趣》第12章 让你立刻爱上数学的8个算术游戏

这章的标题有点夸张，8个游戏就能爱上数学？但有几个游戏我确实以前没听说过。

数字黑洞6174

又称为卡普雷尔卡kaprekar黑洞，我以前用Haskell编程玩了一把。

翻倍，再翻倍！

123456789不断翻倍后，9个数字都只出现1次，一直到第6次翻倍时规律被破坏。

写上一行Haskell源程序验证看看：

take 10 (iterate (*2) 123456789)

结果：[123456789,246913578,493827156,987654312,1975308624,3950617248,7901234496,15802468992,31604937984,63209875968]

唯一的解

用1到9组成一个9位数，第1位能被1整除，前2位能被2整除，前3位能被3整除，…，整个9位数能被9整除。

这样猛的数只有一个：381653729

这里有人给出了一个Haskell程序：

thelist = [1..9]

check [] = False

check xs = (foldl (\x -> \y -> 10*x+y) 0 xs) `mod` (length xs) == 0

onemore [] = [[x] | x <- thelist]

onemore list = [list ++ [l] | l<-thelist,elem l list == False, check (list ++ [l]) == True]

testmore [] = []

testmore (x:xs) = (onemore x) ++ (testmore xs)

result = foldl (.) id (replicate 8 testmore) (onemore [])

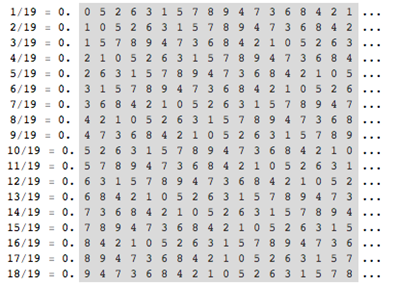
天然形成的幻方

从 1/19 到 18/19 这 18 个分数的小数循环节长度都是 18。把这 18 个循环节排成一个 18×18 的数字阵，恰好构成一个幻方——每一行、每一列和两条对角线上的数字之和都是 81 （注：严格意义上说它不算幻方，因为方阵中有相同数字）

三个神奇的分数

1/49 = 0.0204081632..

100/9899 = 0·01010203050813213455...

100/9801 = 0.0102030405060708091011121314151617181920212223…

这些分数可以用组合数学中的“生成函数”来解释。