AlphaBeta剪枝算法

关于AlphaBeta剪枝的文章太多，这个方法是所有其它搜索方法的基础，得多花些时间认真地理解。

先把基本概念再回顾一遍：

节点：在中国象棋中就是一个棋盘的当前局面Board，当然该轮到谁走棋也是确定的。这里的圆形节点表示终止节点，在中国象棋里就是一方被将死的情况（或者到达了搜索的最大深度），后续不会再有着法产生，游戏如果走到这里就会结束。在引擎里通常给红方一个很大的评估值，如+30000，给黑方一个很小的评估值，如-30000，来方便地判断这种结束局面。（胜利局面有稍微不同的表示法，用-30000+层数ply来表示）

连线：表示一步着法Move，通过这步着法后，局面发生变化，先后手也要交换。

层：通常的术语是ply，复数形式是plies，也有称为levels，当然与depth也是对应的。这个术语是为了与比赛里常说的回合相区分，一个回合通常包含2步，这个ply就表示某一方走了一步。根节点记为0层，以下的层数递增。

深度depth：要注意是从下到上的，还是从上到下的。（1）通常的算法书中都是从下到上递增的，即根节点为最大搜索深度，走到最底部的叶子结点为0，这种算法只要记住一个depth值就可以了。（2）而另一种记法是根部结点为0，越向下depth增加，这时在搜索时就要传递2个参数值，depth和maxDepth，稍微有点啰嗦，应该也会影响一点效率。另外在探查置换表中的结点时，用第（1）种记法也方便一些，因为要知道从当前节点迭代的深度值，否则还要在置换表中保存depth和maxDepth两个值。

 

AlphaBeta剪枝方法是对Minimax方法的优化，它们产生的结果是完全相同的，只不过运行效率不一样。

这种方法的前提假设与Minimax也是一样的：

1）双方都按自己认为的最佳着法行棋。

2）对给定的盘面用一个分值来评估，这个评估值永远是从一方（搜索程序）来评价的，红方有利时给一个正数，黑方有利时给一个负数。（如果红方有利时返回正数，当轮到黑方走棋时，评估值又转换到黑方的观点，如果认为黑方有利，也返回正数，这种评估方法都不适合于常规的算法描述）

3）从我们的搜索程序（通常把它称为Max）看来，分值大的数表示对己方有利，而对于对方Min来说，它会选择分值小的着法。

但要注意：用Negamax风格来描述的AlphaBeta中的评估函数，对轮到谁走棋是敏感的。

也就是说：

在Minimax风格的AlphaBeta算法中，轮红方走棋时，评估值为100，轮黑方走棋评估值仍是100。

但在Negamax风格的AlphaBeta算法中，轮红方走棋时，评估值为100，轮黑方走棋时评估值要为-100。

 

贴一段伪代码：

 

def ABNegaMax (board, depth, maxDepth, alpha, beta)
if ( board.isGameOver() or depth == maxDepth )
    return board.evaluate(), null
bestMove = null
bestScore = -INFINITY
for move in board.getMoves()
    newBoard = board.makeMove(move)
    score = ABNegaMax(newBoard, maxDepth, depth+1, -beta, -max(alpha, bestScore))
    score = -score
    if ( score > bestScore )
        bestScore = score
        bestMove = move
        # early loop exit (pruning)
        if ( bestScore >= beta ) return bestScore, bestMove
return bestScore, bestMove


用下列语句开始调用：

ABNegaMax(board, player, maxDepth, 0, -INFINITY, INFINITY)

// method call with depth 5 and minimum and maximum boundaries
// minimaxValue = alphaBeta(board, 5, -MATE, +MATE)
int alphaBeta(ChessBoard board, int depth, int alpha, int beta)
{
    int value;
    if( depth == 0 || board.isEnded())
    {
         value = evaluate(board);
         return value;
    }
    board.getOrderedMoves();
    int best = -MATE-1;
    int move; 
    ChessBoard nextBoard;
    while (board.hasMoreMoves())
    {
        move = board.getNextMove();
        nextBoard = board.makeMove(move);
        value = -alphaBeta(nextBoard, depth-1,-beta,-alpha);
        if(value > best)
             best = value;
        if(best > alpha)
             alpha = best;
        if(best >= beta)
              break;
     }
     return best;
}

下面这个PDF更清楚地说明了Negamax风格的alphabeta算法的过程：

http://www.cs.colostate.edu/~anderson/cs440/index.html/lib/exe/fetch.php?media=notes:negamax2.pdf

 

 

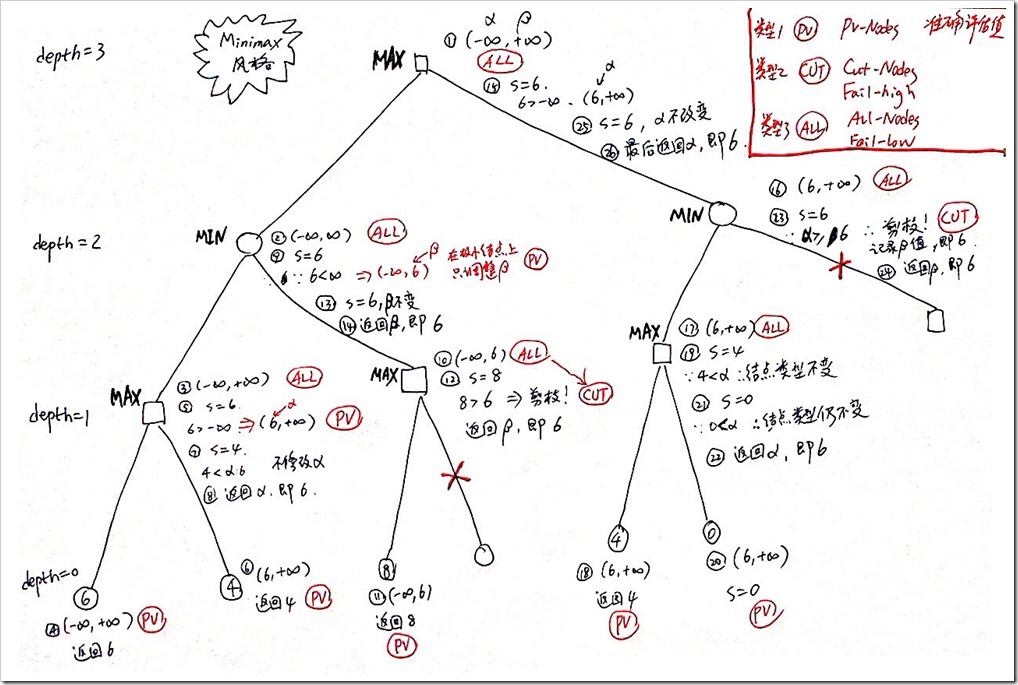
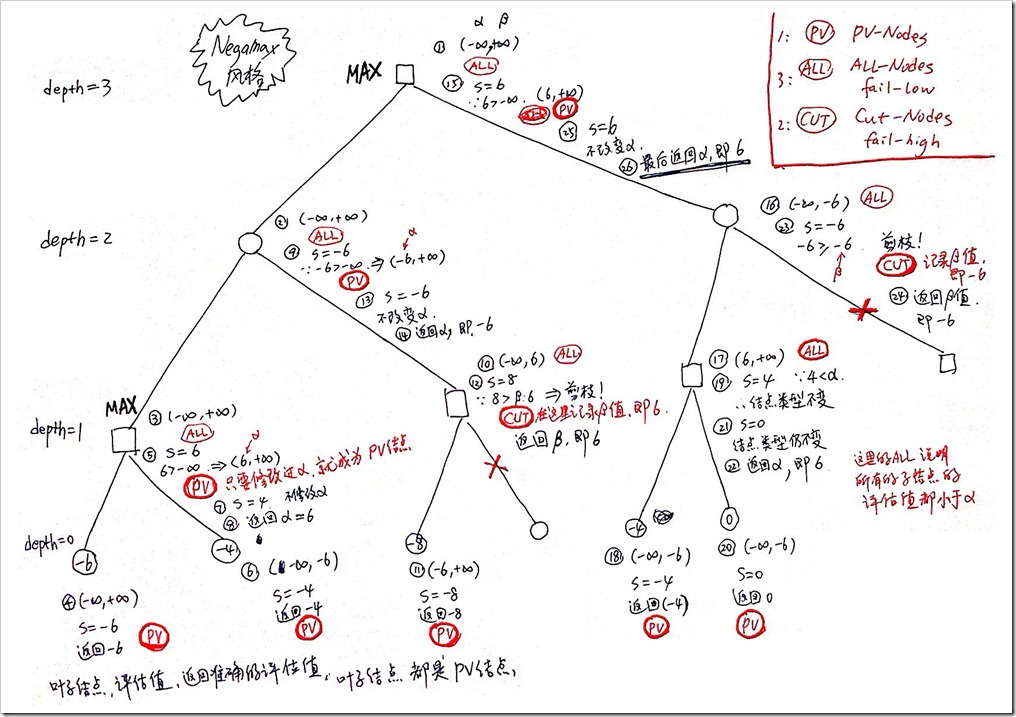
为了更准确地理解minmax和negamax两种不同风格的搜索执行过程，画出了详细的图解，发现negamax更容易理解了，代码也确实精练了不少。

当采用了置换表算法后，还需要对PV-Nodes, Cut-Nodes和All-Nodes三种类型结点的含义以及如何变化有更准确地了解。

 

可以发现，Negamax风格的算法有下面的特点（代码来自象棋巫师）：

        int AlphaBeta(int depth, int alpha, int beta) {
              int hashf = hashfALPHA;    //开始时的结点类型应该是All-Nodes，有些地方称为ALPHA类型结点
              //这里要探查置换表
              if (depth == 0) {   // 叶子结点，评估，写入置换表，返回即可
                 val = Evaluate();
                 RecordHash(depth, val, hashfEXACT); // 叶子结点肯定是PV-Nodes
                 return val;
              }
              GenerateLegalMoves();
              while (MovesLeft()) {
                 MakeNextMove();
                       //注意Negamax风格的调用方式，前面有个负号，后面的参数是-beta和-alpha

               // Negamax的含义中Nega就是指这里的负号
                 val = -AlphaBeta(depth - 1, -beta, -alpha);  
                 UnmakeMove();
                 if (val >= beta) {   // 剪枝情况判断
                    RecordHash(depth, beta, hashfBETA);  //这时的结点类型是Cut-Nodes
                    return beta;
                 }
                 if (val > alpha) {   // Negamax中的max就是指的这一段，要记录最大的评估值，这里没有引入一个新变量，直接就用了alpha变量
                    hashf = hashfEXACT;   // 只要alpha值一发生变化，这个结点类型就是PV-Nodes了！
                    alpha = val;
                 }
               }
               RecordHash(depth, alpha, hashf);
               return alpha;   // 此时的alpha就是记录了当前结点的所有子结点的最大的负评估值！
           }

 

这面的代码在置换表探查方面感觉有点问题，又从Marek Strejczek的论文《Some aspects of chess programming》的第87页上找到一段代码，感觉这段代码充分利用了置换表中存储的信息。

chSCORE alphabetaWithTT(chPOSITION node,chSCORE alpha,beta) {
if (isLeaf(node) ) return evaluate(node);
    if ( (entry = getFromHash(node) ) != NULL) {
        if (TT_entry_deep_enough) {
        // data in hash table comes from a search to the 
        // same depth as current or deeper – so it is reliable
        if (entry.flag == UPPER) {
            if (entry.score <= alpha) {
                return alpha
            }
            if (entry.score < beta)
                beta = flag.score;
            }
        }
        if (entry.flag == LOWER) {
             if (entry.score >= beta) {
                 return beta;
             }
             if (entry.score > alpha) {
                 alpha = flag.score;
             }
         }
         if (entry.flag == EXACT) {
             return entry.score
         }
    }
    else {
        // TT entry represents results of a shallower
        // depth search – no cutoffs possible, but still 
        // a valuable move to try first can be used
        if (entry.move != NULL) {
             try_hash_move_first = true;
        }
    }
}
g = alpha;
x = left_most_child(node);
hash_flag = UPPER;
best_move = NULL;
while (isNotNull (x) ) {
    g = -alphabeta(x, -beta, -alpha);
    if (g > alpha) {
        alpha = g;
        if (g >= beta) {
            hash_flag = LOWER;
            best_move = current_move;
            saveHash(node,g,hash_flag,best_move);
            return beta;
        }
        hash_flag = EXACT;
        best_move = current_move;
    }
    x = next_brother(x);
}
putToHash(node, g, hash_flag, best_move)
return alpha;
} // end of alphabetaWithTT