查找
学习总结(2分)
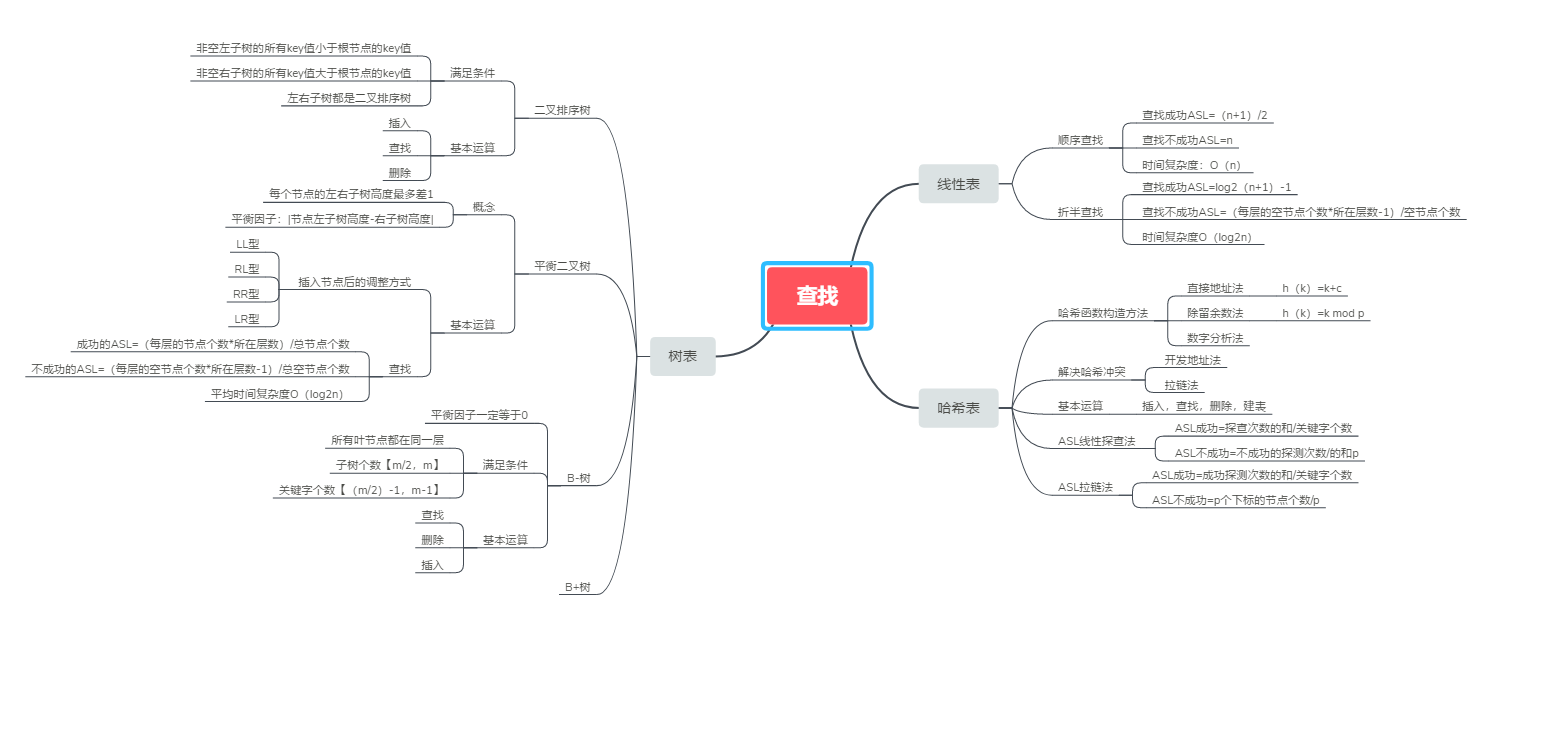
1.1查找的思维导图
1.2 查找学习体会
- 我觉得吧,在查找这章节,从最开始的二叉排序树,到平衡二叉树再到B-树是一个循序渐进地将树平衡优化的过程
- 再这章学习发现对二叉树的操作既要掌握算法,也要会掌握实际是怎么操作,比如二叉排序树的删除插入,然后是平衡二叉树在插入或删除后进行的4种调整(LL,RR,RL,LR),还有B-树插入或删除节点后要进行的树表变化等等
- 哈希表则是以关键字key为自变量,通过一个确定的函数h(k),计算出相应的函数值h(key),作为数据对象的存储地址。但是不同的的关键字会映射相同的地址上,这时就需要解决哈希冲突问题,相应解决方案有换个位置的开发地址法,同个位置的冲突对象组织在一起的链地址法,还有线性探测法,平方探测法等等
2.PTA实验作业(4分)
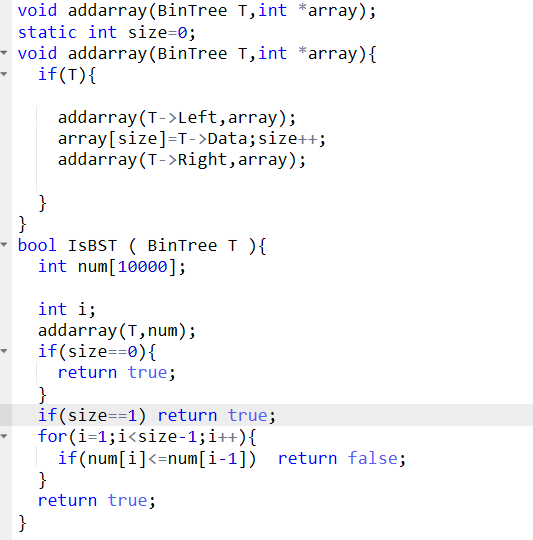
6-2 是否二叉搜索树
设计思路
定义全局变量size
addrray函数{
通过中序遍历把T->data依次存入array数组中
}
IsBST函数{
定义一个存二叉树中序遍历的结果的数组 num[]
调用addrray函数
判断{
size=0为空树返回true
size=1为单节点树返回true
for i=1 to size-1{
遍历数组num
如果数组不是升序排列 返回false
}
否则返回true
}
}
2.3 代码截图
2.4 PTA提交列表说明。
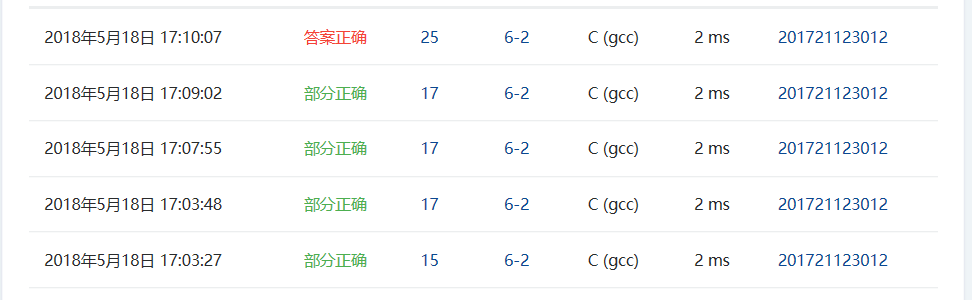
- 第一个错误是没考虑到空树也是特殊的平衡二叉树,然后把size=0时返回true
- 然后是addarray函数的size自增给放在了最后面,以至于中序遍历递归后size并不是树的总的节点数
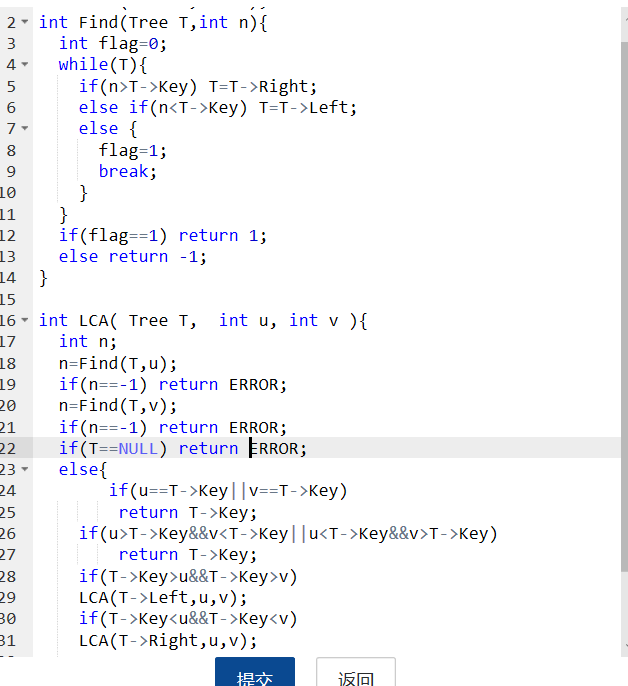
6-3 二叉搜索树中的最近公共祖先
设计思路
LCA函数{
先调用find函数判断u和v是否在树里
如果u和v有一个在二叉树中 返回ERROR
如果是空树返回ERROR
否则{
通过祖先的key值介于v和u之间
从根节点出发若满足T->Key介于u和v之间 返回T->Key
如果u和v都比T->Key大,则往T的右子树找祖先
如果u和v都比T->Key小,则往T的左子树找祖先
}
}
查找find函数{
定义flag=0
while(T不空){
比较n与T->Key大的大小关系:
如果n>T->Key 往T的右子树找
如果n<T->Key 往T的左子树找
否则找到了 flag=1
}
如果(找到了) 返回1
否则返回 -1
}
2.3 代码截图
2.4 PTA提交列表说明。
- 第一次某些测试点没过,是因为太心急简单的以为从根节点出发然后只要满足T->Key介于u和v之间就可以得出两个的最近公共祖先,没考虑到u和v不在二叉树中的情况,用一个find函数先判断u和v是否在树上即正确
7-1 QQ帐户的申请与登陆
设计思路
定义容器map<string,int>p存放账号存在信息
map<string,string>pp 存放账号密码
输入操作次数n
while(n自增) {
依次输入 操作 x , 账号 y 和密码 z
如果 x=L{
if(p[y]=0) 找不到账号
否则{
如果pp[y]!=z 密码错误
否则 登陆成功
}
否则(x=N){
如果(p[y]=1) 账号已存在
否则{
新建账号
p[y]=1
pp[y]=z
申请成功
}
}
}
}
2.3 代码截图

2.4 PTA提交列表说明。
3.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名(截图带自己名字的排名)

3.2 我的总分:
- 120
4. 阅读代码(必做,1分)
bool CheckBST(BinaryTreeNode* pRoot, int min, int max)
{
if(pRoot == NULL)
return true;
if(pRoot->m_nValue < min || pRoot->m_nValue > max)
return false;
return CheckBST(pRoot->m_pLeft, min, pRoot->m_nValue) && CheckBST(pRoot->m_pRight, pRoot->m_nValue, max);
}
bool CheckBST(BinaryTreeNode* pRoot)
{
return CheckBST(pRoot, INT_MIN, INT_MAX);
}
这是判断是否为红黑树的另一种简单解法
- 在该解法中,对于任意结点,所有左边的结点必须小于当前结点,所有右边结点必须大于当前结点,因此可从根结点开始判断,所有结点的值都应该落在一个区间内,自上而下传递区间的最小值和最大值。进入左子树时,更新最大值,进入右子树,更新最小值。
5. 代码Git提交记录截图