CodeForces468B Two Sets 解题报告

题目要求把整数集P的元素分成两部分A与B，A集要求若x在其中，则a-x也必须在其中，B集要求若x在其中，则b-x也必须在其中。这个问题可以建模成一个二分图的完美匹配问题。二分图的左右两个点集都是P，将x与a-x（若存在）连线，将x与b-x（若存在）连线，所求问题就是找该二分图的完美匹配。但是此题如此构造的二分图很特殊，每个顶点的度数至多为2，且连线有限制。所以除了使用二分图完美匹配的通用算法之外，还可以考虑更简单快速的特殊算法。

不妨假设a<b，P为整数集。对P中的元素x，分别称a-x、b-x为x的a补、b补。首先，我们知道，对元素x，若既不存在a补也不存在b补，直接输出“NO”。若只存在a补和b补中的一个，则x与这个补元必定要放到相应的A或B。若a补和b补均存在，这是比较麻烦的情况，我们要决定x到底该放入A还是B。比如a=10，b=12。如果P={4,6,8}，则A={}，B={4,6,8}。如果P={4,6,8,2}，则A={4,6,8,2}，B={}。所以x=4放入A或B都有可能。

为此，先对P中的元素从小到大排序，然后看最小元x，如果x只有一个补元，容易决定x该放入哪个集合。如果这个最小元x的a补和b补都存在呢？有如下结论：x的b补不可能有a补了！（如下图所示）用反证法可证：假设y是b补的a补，即y=a-(b-x)=a-b+x<x，与x是最小元的事实矛盾。

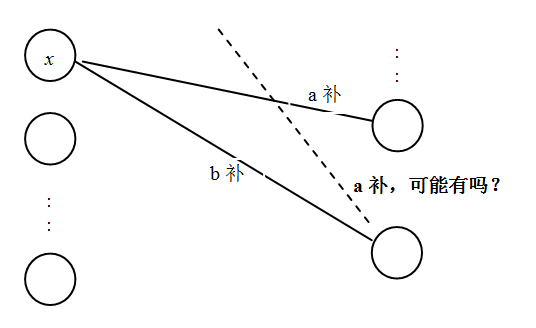
所以在最小元的a补和b补均存在的情况下，虽然不能决定x放哪里，但是可以决定x的b补放哪里，它必定只有b补，故可将b-x以及x一起放入B。然后对P的剩余元素再从最小元开始进行上述检查操作，直至P空为止。

算法需要先对P排序，然后对P进行一趟扫描，每个x需要查找两个补元，二分查找需要O(logn)时间，所以算法的计算复杂性是O(nlogn)。

如果a=b，简单地检查每个元素x，看a-x是否也在P中即可。

  参考代码： 

#include <stdio.h>
#include <set>
#include <vector>
using namespace std;

int main()
{
    int n, a, b, x;
    set<int> P, A;
    set<int>::const_iterator it;
    vector<int> V;
    vector<int>::const_iterator itv;
    bool swap, b1, b2;
        
    scanf("%d%d%d", &n, &a, &b);
    for (int i = 0; i < n; i++) {
        scanf("%d", &x);
        P.insert(x);
        V.push_back(x);
    }
    swap = 0;
    if (a == b) {
        for (it = P.begin(); it != P.end(); it++) {
            x = *it;
            if (P.find(a-x) == P.end()) {
                printf("NO\n");
                return 0;
            }
        }
        A = P;
    } else {
        if (a > b) {
            int t = a;
            a = b;
            b = t;
            swap = 1;
        }
        while (!P.empty()) {
            x = *P.begin();
            b1 = (P.find(a-x) != P.end());
            b2 = (P.find(b-x) != P.end());
            if (!b1 && !b2) {    // x没有补元 
                printf("NO\n");
                return 0;
            } else if (b1 && b2) {    // x有两个补元 
                P.erase(x);
                P.erase(b-x);
            } else {    // x恰有一个补元 
                P.erase(x);
                if (b1) {
                    P.erase(a-x);
                    A.insert(x);
                    A.insert(a-x);
                } else {
                    P.erase(b-x);
                }
            }
        }
    }
    printf("YES\n");
    for (itv = V.begin(); itv != V.end(); itv++)
        printf("%d ", (A.find(*itv) == A.end() ? 1 : 0) ^ swap);
    printf("\n");
    return 0;
}

                            （胡明晓）