概要
前面分别介绍了AVL树"C语言版本"和"C++版本"，本章介绍AVL树的Java实现版本，它的算法与C语言和C++版本一样。内容包括：
1. AVL树的介绍
2. AVL树的Java实现
3. AVL树的Java测试程序
转载请注明出处：http://www.cnblogs.com/skywang12345/p/3577479.html
更多内容: 数据结构与算法系列 目录
(01) AVL树(一)之 图文解析 和 C语言的实现
(02) AVL树(二)之 C++的实现
(03) AVL树(三)之 Java的实现
AVL树的介绍
AVL树是高度平衡的而二叉树。它的特点是：AVL树中任何节点的两个子树的高度最大差别为1。
上面的两张图片，左边的是AVL树，它的任何节点的两个子树的高度差别都<=1；而右边的不是AVL树，因为7的两颗子树的高度相差为2(以2为根节点的树的高度是3，而以8为根节点的树的高度是1)。
AVL树的Java实现
1. 节点
1.1 节点定义
public class AVLTree<T extends Comparable<T>> { private AVLTreeNode<T> mRoot; // 根结点 // AVL树的节点(内部类) class AVLTreeNode<T extends Comparable<T>> { T key; // 关键字(键值) int height; // 高度 AVLTreeNode<T> left; // 左孩子 AVLTreeNode<T> right; // 右孩子 public AVLTreeNode(T key, AVLTreeNode<T> left, AVLTreeNode<T> right) { this.key = key; this.left = left; this.right = right; this.height = 0; } } ...... }
AVLTree是AVL树对应的类，而AVLTreeNode是AVL树节点，它是AVLTree的内部类。AVLTree包含了AVL树的根节点，AVL树的基本操作也定义在AVL树中。AVLTreeNode包括的几个组成对象:
(01) key -- 是关键字，是用来对AVL树的节点进行排序的。
(02) left -- 是左孩子。
(03) right -- 是右孩子。
(04) height -- 是高度。
1.2 树的高度
/* * 获取树的高度 */ private int height(AVLTreeNode<T> tree) { if (tree != null) return tree.height; return 0; } public int height() { return height(mRoot); }
关于高度，有的地方将"空二叉树的高度是-1"，而本文采用维基百科上的定义：树的高度为最大层次。即空的二叉树的高度是0，非空树的高度等于它的最大层次(根的层次为1，根的子节点为第2层，依次类推)。
1.3 比较大小
/* * 比较两个值的大小 */ private int max(int a, int b) { return a>b ? a : b; }
2. 旋转
如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。这种失去平衡的可以概括为4种姿态：LL(左左)，LR(左右)，RR(右右)和RL(右左)。下面给出它们的示意图：
上图中的4棵树都是"失去平衡的AVL树"，从左往右的情况依次是：LL、LR、RL、RR。除了上面的情况之外，还有其它的失去平衡的AVL树，如下图：
上面的两张图都是为了便于理解，而列举的关于"失去平衡的AVL树"的例子。总的来说，AVL树失去平衡时的情况一定是LL、LR、RL、RR这4种之一，它们都由各自的定义：
(1) LL：LeftLeft，也称为"左左"。插入或删除一个节点后，根节点的左子树的左子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。
例如，在上面LL情况中，由于"根节点(8)的左子树(4)的左子树(2)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。
(2) LR：LeftRight，也称为"左右"。插入或删除一个节点后，根节点的左子树的右子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。
例如，在上面LR情况中，由于"根节点(8)的左子树(4)的左子树(6)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。
(3) RL：RightLeft，称为"右左"。插入或删除一个节点后，根节点的右子树的左子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。
例如，在上面RL情况中，由于"根节点(8)的右子树(12)的左子树(10)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。
(4) RR：RightRight，称为"右右"。插入或删除一个节点后，根节点的右子树的右子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。
例如，在上面RR情况中，由于"根节点(8)的右子树(12)的右子树(14)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。
如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。AVL失去平衡之后，可以通过旋转使其恢复平衡，下面分别介绍"LL(左左)，LR(左右)，RR(右右)和RL(右左)"这4种情况对应的旋转方法。
2.1 LL的旋转
LL失去平衡的情况，可以通过一次旋转让AVL树恢复平衡。如下图：
图中左边是旋转之前的树，右边是旋转之后的树。从中可以发现，旋转之后的树又变成了AVL树，而且该旋转只需要一次即可完成。
对于LL旋转，你可以这样理解为：LL旋转是围绕"失去平衡的AVL根节点"进行的，也就是节点k2；而且由于是LL情况，即左左情况，就用手抓着"左孩子，即k1"使劲摇。将k1变成根节点，k2变成k1的右子树，"k1的右子树"变成"k2的左子树"。
LL的旋转代码
/* * LL：左左对应的情况(左单旋转)。 * * 返回值：旋转后的根节点 */ private AVLTreeNode<T> leftLeftRotation(AVLTreeNode<T> k2) { AVLTreeNode<T> k1; k1 = k2.left; k2.left = k1.right; k1.right = k2; k2.height = max( height(k2.left), height(k2.right)) + 1; k1.height = max( height(k1.left), k2.height) + 1; return k1; }
2.2 RR的旋转
理解了LL之后，RR就相当容易理解了。RR是与LL对称的情况！RR恢复平衡的旋转方法如下：
图中左边是旋转之前的树，右边是旋转之后的树。RR旋转也只需要一次即可完成。
RR的旋转代码
/* * RR：右右对应的情况(右单旋转)。 * * 返回值：旋转后的根节点 */ private AVLTreeNode<T> rightRightRotation(AVLTreeNode<T> k1) { AVLTreeNode<T> k2; k2 = k1.right; k1.right = k2.left; k2.left = k1; k1.height = max( height(k1.left), height(k1.right)) + 1; k2.height = max( height(k2.right), k1.height) + 1; return k2; }
2.3 LR的旋转
LR失去平衡的情况，需要经过两次旋转才能让AVL树恢复平衡。如下图：
第一次旋转是围绕"k1"进行的"RR旋转"，第二次是围绕"k3"进行的"LL旋转"。
LR的旋转代码
/* * LR：左右对应的情况(左双旋转)。 * * 返回值：旋转后的根节点 */ private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> k3) { k3.left = rightRightRotation(k3.left); return leftLeftRotation(k3); }
2.4 RL的旋转
RL是与LR的对称情况！RL恢复平衡的旋转方法如下：
第一次旋转是围绕"k3"进行的"LL旋转"，第二次是围绕"k1"进行的"RR旋转"。
RL的旋转代码
/* * RL：右左对应的情况(右双旋转)。 * * 返回值：旋转后的根节点 */ private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> k1) { k1.right = leftLeftRotation(k1.right); return rightRightRotation(k1); }
3. 插入
插入节点的代码
/* * 将结点插入到AVL树中，并返回根节点 * * 参数说明： * tree AVL树的根结点 * key 插入的结点的键值 * 返回值： * 根节点 */ private AVLTreeNode<T> insert(AVLTreeNode<T> tree, T key) { if (tree == null) { // 新建节点 tree = new AVLTreeNode<T>(key, null, null); if (tree==null) { System.out.println("ERROR: create avltree node failed!"); return null; } } else { int cmp = key.compareTo(tree.key); if (cmp < 0) { // 应该将key插入到"tree的左子树"的情况 tree.left = insert(tree.left, key); // 插入节点后，若AVL树失去平衡，则进行相应的调节。 if (height(tree.left) - height(tree.right) == 2) { if (key.compareTo(tree.left.key) < 0) tree = leftLeftRotation(tree); else tree = leftRightRotation(tree); } } else if (cmp > 0) { // 应该将key插入到"tree的右子树"的情况 tree.right = insert(tree.right, key); // 插入节点后，若AVL树失去平衡，则进行相应的调节。 if (height(tree.right) - height(tree.left) == 2) { if (key.compareTo(tree.right.key) > 0) tree = rightRightRotation(tree); else tree = rightLeftRotation(tree); } } else { // cmp==0 System.out.println("添加失败：不允许添加相同的节点！"); } } tree.height = max( height(tree.left), height(tree.right)) + 1; return tree; } public void insert(T key) { mRoot = insert(mRoot, key); }
4. 删除
删除节点的代码
/* * 删除结点(z)，返回根节点 * * 参数说明： * tree AVL树的根结点 * z 待删除的结点 * 返回值： * 根节点 */ private AVLTreeNode<T> remove(AVLTreeNode<T> tree, AVLTreeNode<T> z) { // 根为空 或者 没有要删除的节点，直接返回null。 if (tree==null || z==null) return null; int cmp = z.key.compareTo(tree.key); if (cmp < 0) { // 待删除的节点在"tree的左子树"中 tree.left = remove(tree.left, z); // 删除节点后，若AVL树失去平衡，则进行相应的调节。 if (height(tree.right) - height(tree.left) == 2) { AVLTreeNode<T> r = tree.right; if (height(r.left) > height(r.right)) tree = rightLeftRotation(tree); else tree = rightRightRotation(tree); } } else if (cmp > 0) { // 待删除的节点在"tree的右子树"中 tree.right = remove(tree.right, z); // 删除节点后，若AVL树失去平衡，则进行相应的调节。 if (height(tree.left) - height(tree.right) == 2) { AVLTreeNode<T> l = tree.left; if (height(l.right) > height(l.left)) tree = leftRightRotation(tree); else tree = leftLeftRotation(tree); } } else { // tree是对应要删除的节点。 // tree的左右孩子都非空 if ((tree.left!=null) && (tree.right!=null)) { if (height(tree.left) > height(tree.right)) { // 如果tree的左子树比右子树高； // 则(01)找出tree的左子树中的最大节点 // (02)将该最大节点的值赋值给tree。 // (03)删除该最大节点。 // 这类似于用"tree的左子树中最大节点"做"tree"的替身； // 采用这种方式的好处是：删除"tree的左子树中最大节点"之后，AVL树仍然是平衡的。 AVLTreeNode<T> max = maximum(tree.left); tree.key = max.key; tree.left = remove(tree.left, max); } else { // 如果tree的左子树不比右子树高(即它们相等，或右子树比左子树高1) // 则(01)找出tree的右子树中的最小节点 // (02)将该最小节点的值赋值给tree。 // (03)删除该最小节点。 // 这类似于用"tree的右子树中最小节点"做"tree"的替身； // 采用这种方式的好处是：删除"tree的右子树中最小节点"之后，AVL树仍然是平衡的。 AVLTreeNode<T> min = maximum(tree.right); tree.key = min.key; tree.right = remove(tree.right, min); } } else { AVLTreeNode<T> tmp = tree; tree = (tree.left!=null) ? tree.left : tree.right; tmp = null; } } return tree; } public void remove(T key) { AVLTreeNode<T> z; if ((z = search(mRoot, key)) != null) mRoot = remove(mRoot, z); }
完整的实现代码
AVL树的实现文件(AVRTree.java)
1 /** 2 * Java 语言: AVL树 3 * 4 * @author skywang 5 * @date 2013/11/07 6 */ 7 8 public class AVLTree<T extends Comparable<T>> { 9 private AVLTreeNode<T> mRoot; // 根结点 10 11 // AVL树的节点(内部类) 12 class AVLTreeNode<T extends Comparable<T>> { 13 T key; // 关键字(键值) 14 int height; // 高度 15 AVLTreeNode<T> left; // 左孩子 16 AVLTreeNode<T> right; // 右孩子 17 18 public AVLTreeNode(T key, AVLTreeNode<T> left, AVLTreeNode<T> right) { 19 this.key = key; 20 this.left = left; 21 this.right = right; 22 this.height = 0; 23 } 24 } 25 26 // 构造函数 27 public AVLTree() { 28 mRoot = null; 29 } 30 31 /* 32 * 获取树的高度 33 */ 34 private int height(AVLTreeNode<T> tree) { 35 if (tree != null) 36 return tree.height; 37 38 return 0; 39 } 40 41 public int height() { 42 return height(mRoot); 43 } 44 45 /* 46 * 比较两个值的大小 47 */ 48 private int max(int a, int b) { 49 return a>b ? a : b; 50 } 51 52 /* 53 * 前序遍历"AVL树" 54 */ 55 private void preOrder(AVLTreeNode<T> tree) { 56 if(tree != null) { 57 System.out.print(tree.key+" "); 58 preOrder(tree.left); 59 preOrder(tree.right); 60 } 61 } 62 63 public void preOrder() { 64 preOrder(mRoot); 65 } 66 67 /* 68 * 中序遍历"AVL树" 69 */ 70 private void inOrder(AVLTreeNode<T> tree) { 71 if(tree != null) 72 { 73 inOrder(tree.left); 74 System.out.print(tree.key+" "); 75 inOrder(tree.right); 76 } 77 } 78 79 public void inOrder() { 80 inOrder(mRoot); 81 } 82 83 /* 84 * 后序遍历"AVL树" 85 */ 86 private void postOrder(AVLTreeNode<T> tree) { 87 if(tree != null) { 88 postOrder(tree.left); 89 postOrder(tree.right); 90 System.out.print(tree.key+" "); 91 } 92 } 93 94 public void postOrder() { 95 postOrder(mRoot); 96 } 97 98 /* 99 * (递归实现)查找"AVL树x"中键值为key的节点 100 */ 101 private AVLTreeNode<T> search(AVLTreeNode<T> x, T key) { 102 if (x==null) 103 return x; 104 105 int cmp = key.compareTo(x.key); 106 if (cmp < 0) 107 return search(x.left, key); 108 else if (cmp > 0) 109 return search(x.right, key); 110 else 111 return x; 112 } 113 114 public AVLTreeNode<T> search(T key) { 115 return search(mRoot, key); 116 } 117 118 /* 119 * (非递归实现)查找"AVL树x"中键值为key的节点 120 */ 121 private AVLTreeNode<T> iterativeSearch(AVLTreeNode<T> x, T key) { 122 while (x!=null) { 123 int cmp = key.compareTo(x.key); 124 125 if (cmp < 0) 126 x = x.left; 127 else if (cmp > 0) 128 x = x.right; 129 else 130 return x; 131 } 132 133 return x; 134 } 135 136 public AVLTreeNode<T> iterativeSearch(T key) { 137 return iterativeSearch(mRoot, key); 138 } 139 140 /* 141 * 查找最小结点：返回tree为根结点的AVL树的最小结点。 142 */ 143 private AVLTreeNode<T> minimum(AVLTreeNode<T> tree) { 144 if (tree == null) 145 return null; 146 147 while(tree.left != null) 148 tree = tree.left; 149 return tree; 150 } 151 152 public T minimum() { 153 AVLTreeNode<T> p = minimum(mRoot); 154 if (p != null) 155 return p.key; 156 157 return null; 158 } 159 160 /* 161 * 查找最大结点：返回tree为根结点的AVL树的最大结点。 162 */ 163 private AVLTreeNode<T> maximum(AVLTreeNode<T> tree) { 164 if (tree == null) 165 return null; 166 167 while(tree.right != null) 168 tree = tree.right; 169 return tree; 170 } 171 172 public T maximum() { 173 AVLTreeNode<T> p = maximum(mRoot); 174 if (p != null) 175 return p.key; 176 177 return null; 178 } 179 180 /* 181 * LL：左左对应的情况(左单旋转)。 182 * 183 * 返回值：旋转后的根节点 184 */ 185 private AVLTreeNode<T> leftLeftRotation(AVLTreeNode<T> k2) { 186 AVLTreeNode<T> k1; 187 188 k1 = k2.left; 189 k2.left = k1.right; 190 k1.right = k2; 191 192 k2.height = max( height(k2.left), height(k2.right)) + 1; 193 k1.height = max( height(k1.left), k2.height) + 1; 194 195 return k1; 196 } 197 198 /* 199 * RR：右右对应的情况(右单旋转)。 200 * 201 * 返回值：旋转后的根节点 202 */ 203 private AVLTreeNode<T> rightRightRotation(AVLTreeNode<T> k1) { 204 AVLTreeNode<T> k2; 205 206 k2 = k1.right; 207 k1.right = k2.left; 208 k2.left = k1; 209 210 k1.height = max( height(k1.left), height(k1.right)) + 1; 211 k2.height = max( height(k2.right), k1.height) + 1; 212 213 return k2; 214 } 215 216 /* 217 * LR：左右对应的情况(左双旋转)。 218 * 219 * 返回值：旋转后的根节点 220 */ 221 private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> k3) { 222 k3.left = rightRightRotation(k3.left); 223 224 return leftLeftRotation(k3); 225 } 226 227 /* 228 * RL：右左对应的情况(右双旋转)。 229 * 230 * 返回值：旋转后的根节点 231 */ 232 private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> k1) { 233 k1.right = leftLeftRotation(k1.right); 234 235 return rightRightRotation(k1); 236 } 237 238 /* 239 * 将结点插入到AVL树中，并返回根节点 240 * 241 * 参数说明： 242 * tree AVL树的根结点 243 * key 插入的结点的键值 244 * 返回值： 245 * 根节点 246 */ 247 private AVLTreeNode<T> insert(AVLTreeNode<T> tree, T key) { 248 if (tree == null) { 249 // 新建节点 250 tree = new AVLTreeNode<T>(key, null, null); 251 if (tree==null) { 252 System.out.println("ERROR: create avltree node failed!"); 253 return null; 254 } 255 } else { 256 int cmp = key.compareTo(tree.key); 257 258 if (cmp < 0) { // 应该将key插入到"tree的左子树"的情况 259 tree.left = insert(tree.left, key); 260 // 插入节点后，若AVL树失去平衡，则进行相应的调节。 261 if (height(tree.left) - height(tree.right) == 2) { 262 if (key.compareTo(tree.left.key) < 0) 263 tree = leftLeftRotation(tree); 264 else 265 tree = leftRightRotation(tree); 266 } 267 } else if (cmp > 0) { // 应该将key插入到"tree的右子树"的情况 268 tree.right = insert(tree.right, key); 269 // 插入节点后，若AVL树失去平衡，则进行相应的调节。 270 if (height(tree.right) - height(tree.left) == 2) { 271 if (key.compareTo(tree.right.key) > 0) 272 tree = rightRightRotation(tree); 273 else 274 tree = rightLeftRotation(tree); 275 } 276 } else { // cmp==0 277 System.out.println("添加失败：不允许添加相同的节点！"); 278 } 279 } 280 281 tree.height = max( height(tree.left), height(tree.right)) + 1; 282 283 return tree; 284 } 285 286 public void insert(T key) { 287 mRoot = insert(mRoot, key); 288 } 289 290 /* 291 * 删除结点(z)，返回根节点 292 * 293 * 参数说明： 294 * tree AVL树的根结点 295 * z 待删除的结点 296 * 返回值： 297 * 根节点 298 */ 299 private AVLTreeNode<T> remove(AVLTreeNode<T> tree, AVLTreeNode<T> z) { 300 // 根为空 或者 没有要删除的节点，直接返回null。 301 if (tree==null || z==null) 302 return null; 303 304 int cmp = z.key.compareTo(tree.key); 305 if (cmp < 0) { // 待删除的节点在"tree的左子树"中 306 tree.left = remove(tree.left, z); 307 // 删除节点后，若AVL树失去平衡，则进行相应的调节。 308 if (height(tree.right) - height(tree.left) == 2) { 309 AVLTreeNode<T> r = tree.right; 310 if (height(r.left) > height(r.right)) 311 tree = rightLeftRotation(tree); 312 else 313 tree = rightRightRotation(tree); 314 } 315 } else if (cmp > 0) { // 待删除的节点在"tree的右子树"中 316 tree.right = remove(tree.right, z); 317 // 删除节点后，若AVL树失去平衡，则进行相应的调节。 318 if (height(tree.left) - height(tree.right) == 2) { 319 AVLTreeNode<T> l = tree.left; 320 if (height(l.right) > height(l.left)) 321 tree = leftRightRotation(tree); 322 else 323 tree = leftLeftRotation(tree); 324 } 325 } else { // tree是对应要删除的节点。 326 // tree的左右孩子都非空 327 if ((tree.left!=null) && (tree.right!=null)) { 328 if (height(tree.left) > height(tree.right)) { 329 // 如果tree的左子树比右子树高； 330 // 则(01)找出tree的左子树中的最大节点 331 // (02)将该最大节点的值赋值给tree。 332 // (03)删除该最大节点。 333 // 这类似于用"tree的左子树中最大节点"做"tree"的替身； 334 // 采用这种方式的好处是：删除"tree的左子树中最大节点"之后，AVL树仍然是平衡的。 335 AVLTreeNode<T> max = maximum(tree.left); 336 tree.key = max.key; 337 tree.left = remove(tree.left, max); 338 } else { 339 // 如果tree的左子树不比右子树高(即它们相等，或右子树比左子树高1) 340 // 则(01)找出tree的右子树中的最小节点 341 // (02)将该最小节点的值赋值给tree。 342 // (03)删除该最小节点。 343 // 这类似于用"tree的右子树中最小节点"做"tree"的替身； 344 // 采用这种方式的好处是：删除"tree的右子树中最小节点"之后，AVL树仍然是平衡的。 345 AVLTreeNode<T> min = maximum(tree.right); 346 tree.key = min.key; 347 tree.right = remove(tree.right, min); 348 } 349 } else { 350 AVLTreeNode<T> tmp = tree; 351 tree = (tree.left!=null) ? tree.left : tree.right; 352 tmp = null; 353 } 354 } 355 356 return tree; 357 } 358 359 public void remove(T key) { 360 AVLTreeNode<T> z; 361 362 if ((z = search(mRoot, key)) != null) 363 mRoot = remove(mRoot, z); 364 } 365 366 /* 367 * 销毁AVL树 368 */ 369 private void destroy(AVLTreeNode<T> tree) { 370 if (tree==null) 371 return ; 372 373 if (tree.left != null) 374 destroy(tree.left); 375 if (tree.right != null) 376 destroy(tree.right); 377 378 tree = null; 379 } 380 381 public void destroy() { 382 destroy(mRoot); 383 } 384 385 /* 386 * 打印"二叉查找树" 387 * 388 * key -- 节点的键值 389 * direction -- 0，表示该节点是根节点; 390 * -1，表示该节点是它的父结点的左孩子; 391 * 1，表示该节点是它的父结点的右孩子。 392 */ 393 private void print(AVLTreeNode<T> tree, T key, int direction) { 394 if(tree != null) { 395 if(direction==0) // tree是根节点 396 System.out.printf("%2d is root\n", tree.key, key); 397 else // tree是分支节点 398 System.out.printf("%2d is %2d's %6s child\n", tree.key, key, direction==1?"right" : "left"); 399 400 print(tree.left, tree.key, -1); 401 print(tree.right,tree.key, 1); 402 } 403 } 404 405 public void print() { 406 if (mRoot != null) 407 print(mRoot, mRoot.key, 0); 408 } 409 }
AVL树的测试程序(AVLTreeTest.java)
1 /** 2 * Java 语言: AVL树 3 * 4 * @author skywang 5 * @date 2013/11/07 6 */ 7 8 public class AVLTreeTest { 9 private static int arr[]= {3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9}; 10 11 public static void main(String[] args) { 12 int i; 13 AVLTree<Integer> tree = new AVLTree<Integer>(); 14 15 System.out.printf("== 依次添加: "); 16 for(i=0; i<arr.length; i++) { 17 System.out.printf("%d ", arr[i]); 18 tree.insert(arr[i]); 19 } 20 21 System.out.printf("\n== 前序遍历: "); 22 tree.preOrder(); 23 24 System.out.printf("\n== 中序遍历: "); 25 tree.inOrder(); 26 27 System.out.printf("\n== 后序遍历: "); 28 tree.postOrder(); 29 System.out.printf("\n"); 30 31 System.out.printf("== 高度: %d\n", tree.height()); 32 System.out.printf("== 最小值: %d\n", tree.minimum()); 33 System.out.printf("== 最大值: %d\n", tree.maximum()); 34 System.out.printf("== 树的详细信息: \n"); 35 tree.print(); 36 37 i = 8; 38 System.out.printf("\n== 删除根节点: %d", i); 39 tree.remove(i); 40 41 System.out.printf("\n== 高度: %d", tree.height()); 42 System.out.printf("\n== 中序遍历: "); 43 tree.inOrder(); 44 System.out.printf("\n== 树的详细信息: \n"); 45 tree.print(); 46 47 // 销毁二叉树 48 tree.destroy(); 49 } 50 }
AVL树的Java测试程序
AVL树的测试程序运行结果如下：
== 依次添加: 3 2 1 4 5 6 7 16 15 14 13 12 11 10 8 9 == 前序遍历: 7 4 2 1 3 6 5 13 11 9 8 10 12 15 14 16 == 中序遍历: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 == 后序遍历: 1 3 2 5 6 4 8 10 9 12 11 14 16 15 13 7 == 高度: 5 == 最小值: 1 == 最大值: 16 == 树的详细信息: 7 is root 4 is 7's left child 2 is 4's left child 1 is 2's left child 3 is 2's right child 6 is 4's right child 5 is 6's left child 13 is 7's right child 11 is 13's left child 9 is 11's left child 8 is 9's left child 10 is 9's right child 12 is 11's right child 15 is 13's right child 14 is 15's left child 16 is 15's right child == 删除根节点: 8 == 高度: 5 == 中序遍历: 1 2 3 4 5 6 7 9 10 11 12 13 14 15 16 == 树的详细信息: 7 is root 4 is 7's left child 2 is 4's left child 1 is 2's left child 3 is 2's right child 6 is 4's right child 5 is 6's left child 13 is 7's right child 11 is 13's left child 9 is 11's left child 10 is 9's right child 12 is 11's right child 15 is 13's right child 14 is 15's left child 16 is 15's right child
下面，我们对测试程序的流程进行分析！
1. 新建AVL树
2. 依次添加"3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9" 到AVL树中。
2.01 添加3,2
添加3,2都不会破坏AVL树的平衡性。
2.02 添加1
添加1之后，AVL树失去平衡(LL)，此时需要对AVL树进行旋转(LL旋转)。旋转过程如下：
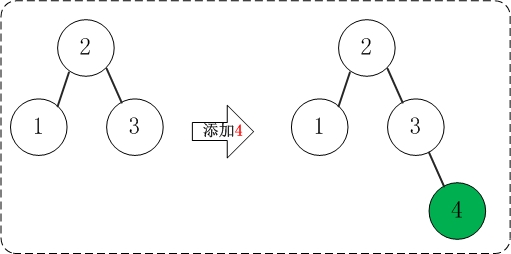
2.03 添加4
添加4不会破坏AVL树的平衡性。
2.04 添加5
添加5之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：
2.05 添加6
添加6之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：
2.06 添加7
添加7之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：
2.07 添加16
添加16不会破坏AVL树的平衡性。
2.08 添加15
添加15之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：
2.09 添加14
添加14之后，AVL树失去平衡(RL)，此时需要对AVL树进行旋转(RL旋转)。旋转过程如下：
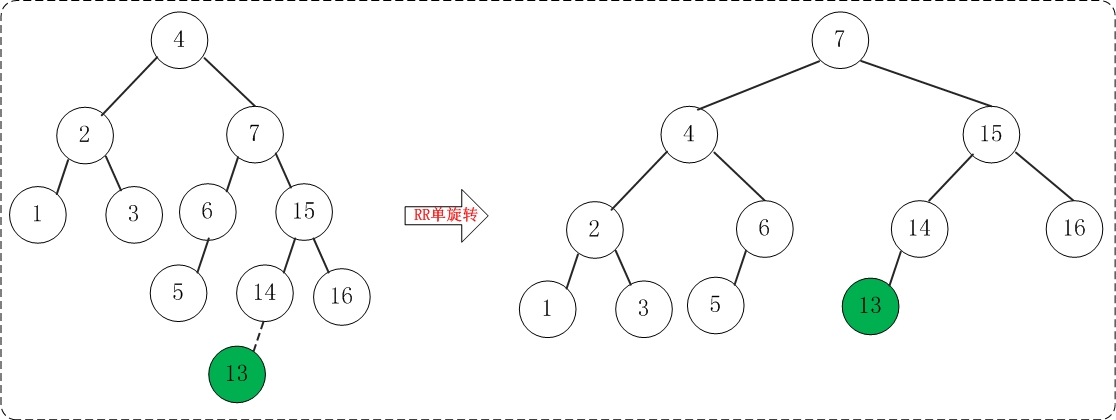
2.10 添加13
添加13之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：
2.11 添加12
添加12之后，AVL树失去平衡(LL)，此时需要对AVL树进行旋转(LL旋转)。旋转过程如下：
2.12 添加11
添加11之后，AVL树失去平衡(LL)，此时需要对AVL树进行旋转(LL旋转)。旋转过程如下：
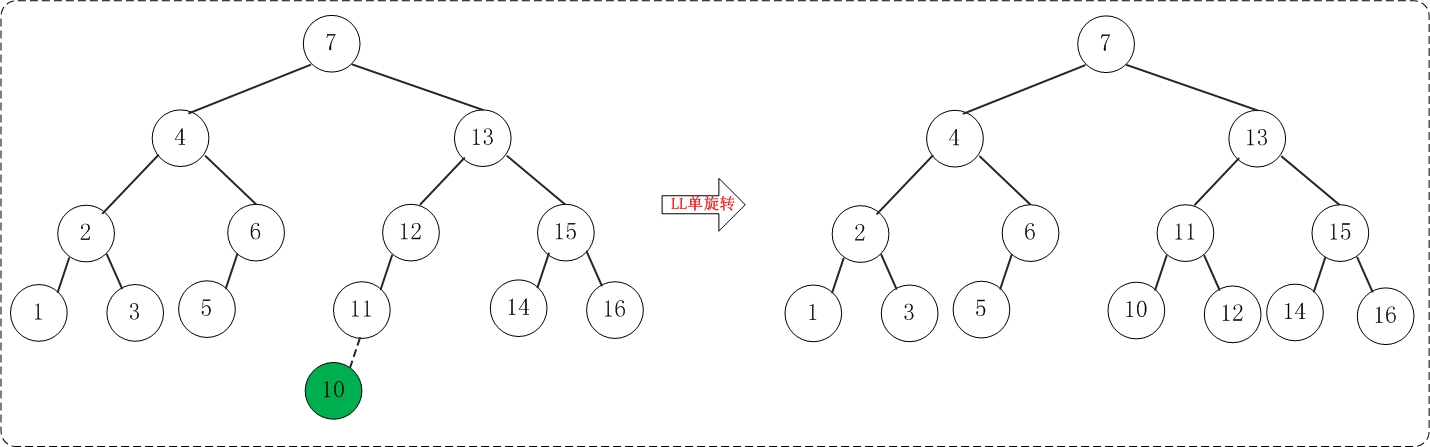
2.13 添加10
添加10之后，AVL树失去平衡(LL)，此时需要对AVL树进行旋转(LL旋转)。旋转过程如下：
2.14 添加8
添加8不会破坏AVL树的平衡性。
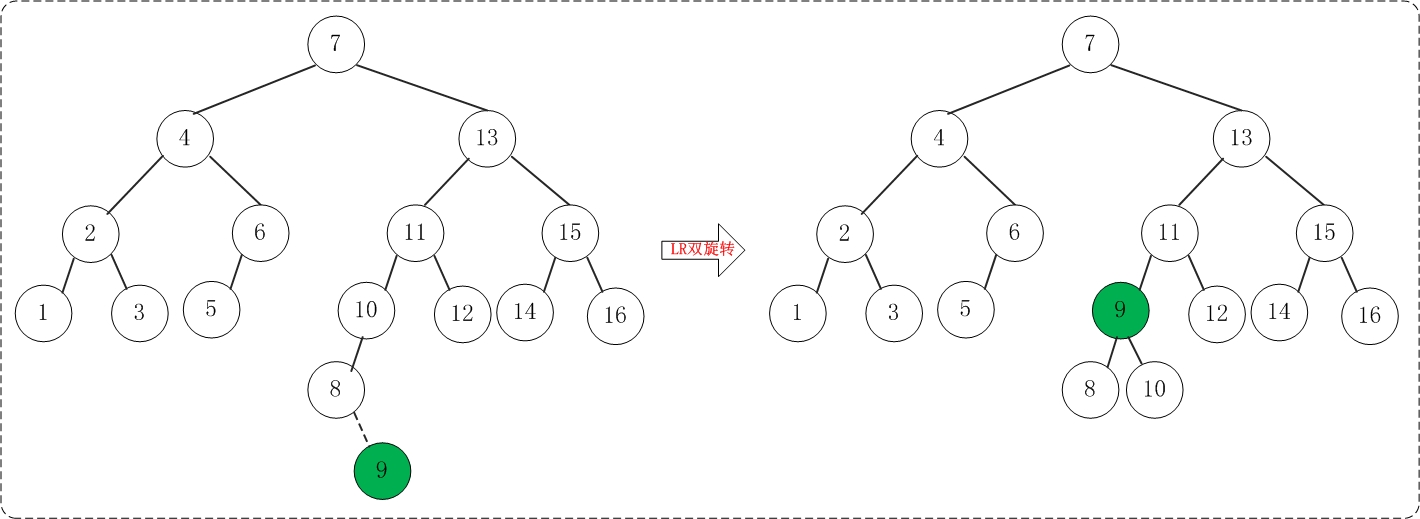
2.15 添加9
但是添加9之后，AVL树失去平衡(LR)，此时需要对AVL树进行旋转(LR旋转)。旋转过程如下：
3. 打印树的信息
输出下面树的信息：
前序遍历: 7 4 2 1 3 6 5 13 11 9 8 10 12 15 14 16
中序遍历: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
后序遍历: 1 3 2 5 6 4 8 10 9 12 11 14 16 15 13 7
高度: 5
最小值: 1
最大值: 16
4. 删除节点8
删除操作并不会造成AVL树的不平衡。
删除节点8之后，再打印该AVL树的信息。
高度: 5
中序遍历: 1 2 3 4 5 6 7 9 10 11 12 13 14 15 16
