前言
我们知道,多项式定义为:
![]()
在几何学中,多项式是最简单的平滑曲线。简单是指它仅由乘法及加法构成,平滑是因为它类同口语中的平滑,以数学术语来说,它是无限可微,即它的所有高次微分都存在。事实上,多项式的微分也是多项式。简单及平滑的特点,使多项式在数值分析、图论,以及电脑绘图等,都发挥极大的作用。多项式求值是解决许多问题的核心技术。以数值分析为例,多项式函数常常用作对数学库中的三角函数求近似值。
现在,让我们来用 C 语言写一个对多项式求值的函数吧。
直接的算法
直接按照多项式的定义使用循环求值:
double poly(double a[], double x)
{
double result = 0, p = 1;
for (int i = 0; i < N; i++, p *= x) result += a[i] * p;
return result;
}
这个算法需要执行 2N 个乘法和 N 个加法。
秦九韶算法(Horner's method)
我们可以通过使用秦九韶算法,或者被大多数外国人以及一些中国人称为 Horner's method 的算法,来减少乘法的数量:
![]()
相应的 C 语言程序如下所示:
double polyh(double a[], double x)
{
double result = 0;
for (int i = N - 1; i >= 0; i--) result = result * x + a[i];
return result;
}
这个算法需要执行 N 个乘法和 N 个加法。乘法的数量是原始算法的一半。
看来,通过使用秦九韶算法,我们大大地优化了程序的性能。
且慢,还是以事实说话吧,让我们来作一些测试吧。
测试程序
下面就是比较这两个算法性能优劣的测试程序 poly.c :
#include <stdio.h>
#include <time.h>
#define N 23456789
void initialize(double a[])
{
for (int i = 0; i < N; i++) a[i] = i - 12345678.9012345;
}
double poly(double a[], double x)
{
double result = 0, p = 1;
for (int i = 0; i < N; i++, p *= x) result += a[i] * p;
return result;
}
double polyh(double a[], double x)
{
double result = 0;
for (int i = N - 1; i >= 0; i--) result = result * x + a[i];
return result;
}
int main(int argc, char *argv[])
{
static double a[N];
initialize(a);
double result = 0, (*func)(double*, double) = (argc > 1) ? polyh : poly;
clock_t elapsed = clock();
for (int i = 0; i < 1234; i++) result += func(a, 2.34 / (i - 1234567) - 1);
elapsed = clock() - elapsed;
printf("%p %g %11f\n", func, result, (double)elapsed / CLOCKS_PER_SEC);
}
这个测试程序通过对一个二十多万项的多项式用不同的自变量值求值一千多遍来比较两个算法的优劣。测试程序中的各项参数经过精心选择,不会在求值过程中造成浮点溢出。在 C 语言中,每个双精度浮点数占用八个字节,所以这个测试程序大约需要一百八十兆字节的内存空间来运行。
测试结果
我们在 32-bit Windows 操作系统和 64-bit Linux 操作系统下均进行了测试,结果如下所示:
D:\work> cl /O2 poly.cpp 用于 80x86 的 Microsoft (R) 32 位 C/C++ 优化编译器 16.00.40219.01 版 版权所有(C) Microsoft Corporation。保留所有权利。 poly.cpp Microsoft (R) Incremental Linker Version 10.00.40219.01 Copyright (C) Microsoft Corporation. All rights reserved. /out:poly.exe poly.obj D:\work> poly 00871000 1.4271e+029 107.531000 D:\work> poly h 00871080 1.4271e+029 127.686000 D:\work> poly h 00871080 1.4271e+029 127.686000 D:\work> poly 00871000 1.4271e+029 106.860000 D:\work> poly 00871000 1.4271e+029 107.935000 D:\work> poly h 00871080 1.4271e+029 128.662000
ben@vbox:~/work> gcc -std=c99 -O2 poly.c ben@vbox:~/work> ./a.out 0x400640 1.4271e+29 125.240000 ben@vbox:~/work> ./a.out 0x400640 1.4271e+29 124.820000 ben@vbox:~/work> ./a.out h 0x400680 1.4271e+29 160.890000 ben@vbox:~/work> ./a.out h 0x400680 1.4271e+29 162.210000 ben@vbox:~/work> ./a.out 0x400640 1.4271e+29 125.450000 ben@vbox:~/work> ./a.out h 0x400680 1.4271e+29 162.230000
上述运行结果中,第一栏是 func 变量的值,表示指向 poly 或 polyh 函数的指针。第二栏是对多项式求值结果的总和。第三栏是运行时间,单位是秒。总结一下,如下表所示:
| 操作系统 | Windows (32-bit) | Linux (64-bit) | ||
| 所用算法 | 直接的 | 秦九韶 | 直接的 | 秦九韶 |
| 函数地址 | 00871000 | 00871080 | 0x400640 | 0x400680 |
| 计算结果 | 1.4271e+029 | 1.4271e+029 | 1.4271e+29 | 1.4271e+29 |
| 1 | 107.531 | 127.686 | 125.24 | 160.89 |
| 2 | 106.860 | 127.686 | 124.82 | 162.21 |
| 3 | 107.935 | 128.662 | 125.45 | 162.23 |
| 平均(秒) | 107.442 | 128.011 | 125.17 | 161.78 |
测试说明
是不是非常意外?无论是在 32-bit Windows 操作系统,还是在 64-bit Linux 操作系统中测试,多次测试结果都表明秦九韶算法比原始的算法慢,同一算法在同一操作系统中的多次运行的所需的时间也很接近。由于我们使用的 Linux 操作系统是 64-bit 的,同一算法比在 32-bit 的 Windows 操作系统运行要稍微慢一点。所有的测试结果中,无论是用哪种算法,还是在不同的操作系统中,对多项式求值结果的总和都是相同的,这是预料之中,如果不同就有问题了。
下图是测试程序运行时的内存和 CPU 使用情况,由于是双核的 CPU,测试程序运行时 CPU 使用率为百分之五十左右:
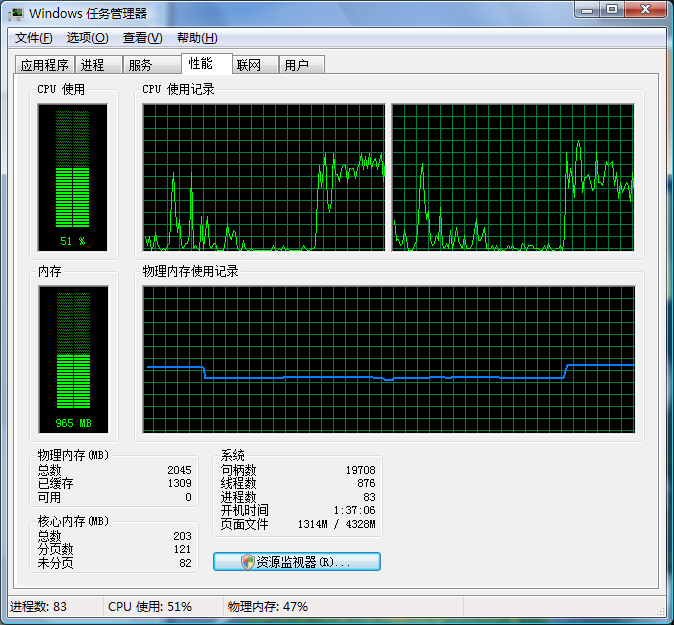
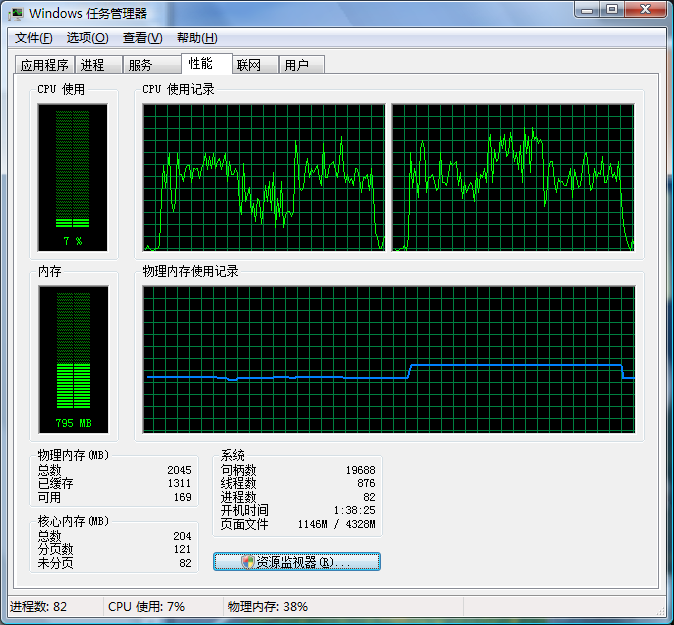
可以看出进程数为83个,内存使用965MB。测试程序运行完毕,进程数减少一个,内存也降到795MB:
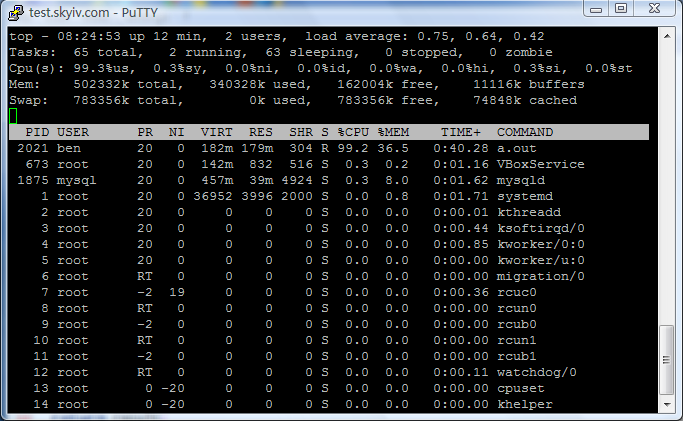
下图是在 Linux 操作系统中测试程序的运行状况,由于 VirtualBox 只给 Linux 操作系统分配一个 CPU,所以测试程序运行时 CPU 占用接近百分之百,内存占用大约 179 MB,如下图所示:
测试环境
本次测试是在 Dell inspiron 1520 本本上运行的,该本本只有一个 CPU,是双核心的 Intel Core2 Duo。安装了 Windows Vista Hoem Premium SP2 (32-bit) 操作系统。

在 Oracle VM VirtualBox 上运行的 openSuSE 12.1 (64-bit) 操作系统:
结论
通过以上论述,说明了最小化一个计算中的操作数量不一定会提高它的性能。至于出现这个情况的原因,敬请期待本文的下篇。




