条件随机场（三）

接上一篇文章，本篇讲述两种概率模型的图表示(Graphical Representation)，为此，引入概率图模型的概念。

概率图模型是概率分布的图形表示。图中每个结点表示一个随机变量，结点之间的边表示两个结点之间的依赖性，即对应两个随机变量是直接相关的，如果结点之间没有边存在，则对应两个随机变量是条件独立的，比如随机变量a和b在随机变量c的条件下独立，则有$p(a,b|c)=p(a|c)p(b|c)$，即事件c发生后，事件a与事件b独立。

条件独立可以将很复杂的概率模型分解成一个个连乘的因子，每个因子中对应的随机变量是原来图中随机变量的子集，因为这些因子对应的随机变量子集之间条件独立，所以可以将联合概率写成因子的连乘，也称因子分解。假设概率图为G=(V,E)，V表示所有结点，E表示所有边，根据前面条件随机场（一）的介绍，图G可以分解为各个最大团的组合，假设最大团对应结点结合S，V所表示的所有随机变量为$\vec v$，S所表示的所有随机变量为$\vec {v}_s$，最大团对应的因子设为$\Psi_s$，那么V的所有随机变量的联合概率分布为，

\begin{equation} p(\vec v) = \prod_{s} \Psi_s (\vec {v}_s) \end{equation}

 令概率图结点$V=X \bigcup Y$，其中X表示输入随机变量，Y表示输出随机变量。这里介绍一下几个核心的概念，概率图模型（probabilistic graphical model）可以分为两种：independency graph和factor graph。independency graph直接描述了变量的条件独立，而factor graph则是通过因子分解（ factorization）的方式暗含变量的条件独立。factor graph图中圆圈点也表示随机变量，另外还多了一个实心小方块，表示因子结点（factor node），factor graph的边总是无向的，将随机变量与结点与因子结点连接起来。因子$\Psi_s$包含了那些与因子结点有边连接的结点所对应的随机变量，如下右图，所以factor graph是一种概率分布的因子分解的图形表示。

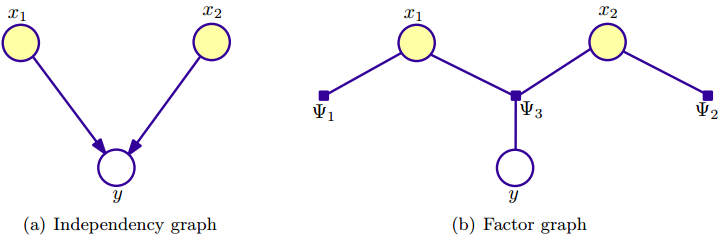
例如，假设联合概率分布$p(x_1,x_2,y)$可以因子分解为$p(\vec x,y)=p(x_1)p(x_2)p(y|x_1,x_2)$，其中各因子项为$\Psi_1 (x_1)=p(x_1), \quad \Psi_2 (x_2)=p(x_2), \quad \Psi_3 (y)=p(y|x_1,x_2)$，这里$x_1,x_2$相互独立。这个概率模型就对应上面两个概率图。

 有向图模型

联合概率分布$p(\vec v)$可以因子分解为条件分布的连乘，每个因子表示结点$v_k$，其条件分布的条件是一系列的父结点$v_{k}^p$，

\begin{equation} p(\vec v) = p(v_1)p(v_2|v_1)...p(v_K|v_{K-1},v_{K-2},...,v_1) = \prod_{k=1}^K p(v_k | v_{k}^p) \end{equation}

如下图所示是一个贝叶斯模型，

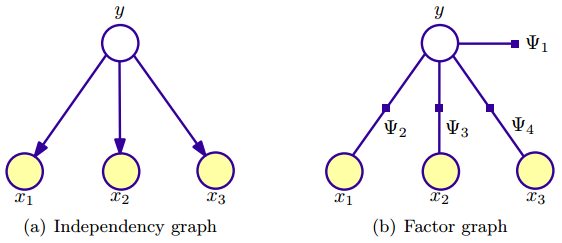
其中有三个输入（观测）变量，概率分布可以因子分解为$p(y,x_1,x_2,x_3)=p(y)p(x_1|y)p(x_2|y,x_1)p(x_3|y,x_1,x_2)=p(y)p(x_1|y)p(x_2)p(x_3|y)$，其中第二个等号的推导用到了朴素贝叶斯假设，即输入x 的分量在输出y 的条件下独立。对应于factor graph，则各因子项为$\Psi_1=p(y)$，$\Psi_2=p(x_1|y)$，$\Psi_3=p(x_2|y)$，$\Psi_4=p(x_3|y)$，怎么样，是不是跟图表示很吻合？

类似地，再给出一个例子如下图，这是一个HMM分类器模型，输入（观测）序列为$x_1,x_2,x_3$，输出（分类）序列为$y_1,y_2,y_3$，

从上图(a)中可以发现，输入变量x 之间在给定输出y的条件下独立，而输出变量y则仅依赖前一个输出，于是我们可以直接写出概率分布为$p(x_1,x_2,x_3,y_1,y_2,y_3)=p(y_1)p(x_1|y_1)p(y_2|y_1)p(x_2|y_2)p(y_3|y_2)p(x_3|y_3)$，各因子项为$\Psi_1=p(y_1), \Psi_2=p(x_1|y_1), \Psi_3=p(x_2|y_2), \Psi_4=p(x_3|y_3), \Psi_5=p(y_2|y_1), \Psi_6=p(y_3|y_2)$。

无向图模型

概率分布也可以使用无向图表示，即概率图G上的所有最大团C上的非负函数连乘，这部分内容可以参考前面讲的条件随机场（一），可以这么做的主要原因是最大团之间的条件独立性，即全局马尔可夫性，于是概率分布为

\begin{equation} p(\vec v) = \frac 1 Z \prod_{C \in \mathcal C} \Psi_C (\vec {v}_C) \end{equation}

其中$\Psi_C \geq 0$，称为势函数（potential function），对应于随机变量组$\vec {v}_C$，$C \in \mathcal C$是无向图G上最大团。

对比有向图中则是联合概率分布因子分解成条件概率的连乘，无向图则是最大团的势函数的连乘，势函数可以不是概率函数（对随机变量求和或积分可以不为1），所以需要势函数的连乘需要归一化，也就是上式中的归一化因子Z，

\begin{equation} Z= \sum_{\vec v} \prod_{C \in \mathcal C} \Psi_C (\vec {v}_C) \end{equation}

其中对向量$\vec v$的求和，$\vec v$的取值为所有可能的随机变量组的值。

在条件随机场（二）中，我们讲到最大熵模型的概率分布可以写为非负势函数的连乘，如下，

\begin{equation} p_{\vec{\lambda}}(y|x)= \frac 1 {Z_{\vec{\lambda}}(x)} \prod_{i=1}^m \exp (\lambda_i f_i (x,y)) \end{equation}

上式这个对数线性模型中，势函数为权值特征（$\lambda_i$为特征函数f_i(x,y)的权重）的指数函数。通常就是采用这种形式的势函数，因为它满足势函数严格正（strict positivity）的要求。下图所示为最大熵模型的两种图表示，观测变量x 只有一个，如(a)图，

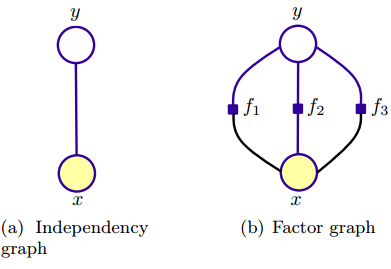
与朴素贝叶斯模型不同，最大熵模型从整体来建模，“保留尽可能多的不确定性，在没有更多的信息时，不擅自做假设”，特征函数则可看作是人为赋给模型的信息，表示特征 x 与 y 的某种相关性，比如上图中，x与y之间有三个特征函数。有向图无法表示这种相关性，则采用无向图表示最大熵模型。

有向图和无向图区别在于如何将原始的概率分布进行因子分解。有向图因子分解成条件概率的连乘，无向图采用势函数的连乘，且需要归一化，没有明确指定随机变量之间的关联性，而是通过加权特征函数来参与计算。

条件随机场

根据前面的介绍，我们知道隐马尔可夫是朴素贝叶斯的序列扩展（单个分类扩展到分类序列），同样地，条件随机场可以理解为最大熵模型的单个分类扩展到分类序列。条件随机场与HMM一样都是判别模型（计算$p(\vec y| \vec x)$而非$p(y|x)$）。然而，条件随机场不一定是HMM那样的对数线性结构，而可以是任意结构（虽然最后还是会着重讨论线性链条件随机场）。

给定输入$\vec x = (x_1,...,x_n)$，条件随机场模型计算输出$\vec y = (y_1,...,yn)$的条件概率$p(\vec y | \vec x)$，注意这里向量$\vec x, \vec y$表示序列，其中输入序列也称观测序列。条件随机场模型的一般形式与无向图的概率分布一样，见上文，

\begin{equation} p(\vec v) = \frac 1 Z \prod_{C \in \mathcal C} \Psi_C (\vec {v}_C) \end{equation}

于是条件概率可写为，

\begin{equation} \begin{aligned} p(\vec {y} | \vec {x}) & = \frac {p(\vec {x} , \vec {y})} {p(\vec {x})} \\ & = \frac {p(\vec {x} , \vec {y})} {\sum_{{\vec {y}}^{'}} p({\vec {y}}^{'}, \vec x)} \\ & = \frac {\frac 1 Z \prod_{C \in \mathcal C} \Psi_C (\vec{x}_C, \vec{y}_C)} {\frac 1 Z \sum_{{\vec{y}}^{'}} \prod_{C \in \mathcal C} \Psi_C (\vec{x}_C, {\vec{y}_{C}}^{'})} \end{aligned} \end{equation}

于是CRF的一般形式为，

\begin{equation}  p(\vec {y} | \vec {x}) = \frac 1 {Z(\vec x)} \prod_{C \in \mathcal {C}} \Psi_C (\vec{x}_C, \vec{y}_C) \end{equation}

其中，

\begin{equation} Z(\vec x) = \sum_{{\vec y}^{'}} \prod_{C \in \mathcal C} \Psi_C (\vec{x}_C, {\vec{y}_{C}}^{'}) \end{equation}

如上文所述，$\Psi_C$是最大团上的函数。

下图是一个线性链CRF的例子，每个因子对应一个势函数，势函数将不同的特征函数结合起来，而特征函数则体现了相应的观测和输出之间的关联。

线性链CRF

线性链CRF是CRF的特殊形式，其无向图是线性链结构，输出变量为一个序列，如下图所示，

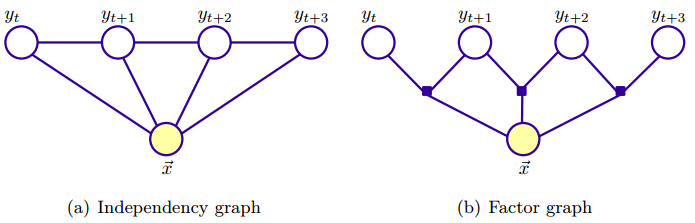
根据上面(8)式和图(b)，可知线性链CRF概率分布可写为

\begin{equation} p(\vec y | \vec x) = \frac 1 {Z(\vec x)} \prod_{j=1}^n \Psi_j (\vec x, \vec y) \end{equation}

 其中，

\begin{equation} Z(\vec x) = \sum_{{\vec y}^{'}} \prod_{j=1}^n \Psi_j (\vec x, {\vec y}^{'}) \end{equation}

为了防止遗忘前面的推导细节，这里再备注一下：上式对${\vec y}'$的求和是对$\mathcal Y$空间上所有向量取值求和。理解(11)式其实并不难，根据(8)式我们知道概率分布为各个最大团上的函数连乘，根据上图，我们知道这里最大团就是$(\vec x, y_{i-1}, y_i)$，其中包含了三个结点，于是再根据(3)式和(5)式，最大团上的函数为

\begin{equation} \Psi_j (\vec x, \vec y) = \exp (\sum_{i=1}^m \lambda_i f_i (y_{j-1}, y_j, \vec x, j)) \end{equation}

（其实，这里最大团$(\vec x, y_{i-1}, y_i)$上的函数$\Psi_j (\vec x, \vec y)$中的指数部分是一个m个特征函数值的求和，m个特征函数包含两部分：1. 转移特征；2.状态特征）

上式中 m 表示总共有 m 个特征函数。假设观测序列长度为 n + 1（注意指的是 y 的长度，拿中文分词来说，这里模型要解决的问题就是已知输入x 为状态，求输出 y 序列出现的条件概率），那么就有 n 个最大团，于是将上式代入(11)式，得

\begin{equation} p_{\vec {\lambda}}(\vec y | \vec x) = \frac 1 {Z_{\vec {\lambda}} (\vec x)} exp(\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y_{j-1}, y_j, \vec x, j)) \end{equation}

且有

\begin{equation} Z_{\vec {\lambda}}(\vec x) =  \sum_{y \in \mathcal Y} exp(\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y_{j-1}, y_j, \vec x, j)) \end{equation}

$Z_{\vec {\lambda}}(\vec x)$中的对$\vec y$的求和是针对 $\mathcal Y$中所有可能的序列。

上两式计算中，我们假设了$\vec y = (y_0, y_1,...,y_n)$，特征函数的参数包含了下标 j，因为与最大熵模型不同，这里输出是一个序列。特征函数的权重$\lambda_i$与下标 j 是无关的。

 在(13)式中，将对 j 求和移到指数的左边，根据指数的特性，求和则转为连乘，于是有

\begin{equation} p_{\vec {\lambda}}(\vec y | \vec x) = \frac 1 {Z_{\vec {\lambda}} (\vec x)} \prod_{j=1}^n exp( \sum_{i=1}^m \lambda_i f_i (y_{j-1}, y_j, \vec x, j)) \end{equation}

当然，将(13)式中对 i 求和移到指数的左边则为

\begin{equation} p_{\vec {\lambda}}(\vec y | \vec x) = \frac 1 {Z_{\vec {\lambda}} (\vec x)} \prod_{i=1}^m exp( \sum_{j=1}^n \lambda_i f_i (y_{j-1}, y_j, \vec x, j)) \end{equation}

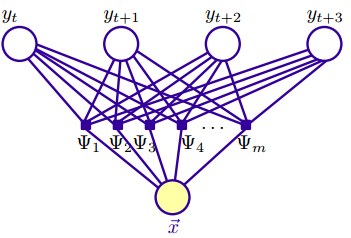
于是根据上式，变成对特征上的函数项连乘，函数项表达式为

$$\Psi_i = exp(\sum_{j=1}^n \lambda_i f_i (y_{j-1},y_j, \vec x, j))$$

如下图可以帮助理解上式。

甚至还可以这样转换(13)式，

\begin{equation} p_{\vec {\lambda}}(\vec y | \vec x) = \frac 1 {Z_{\vec {\lambda}} (\vec x)} \prod_{i=1}^m \prod_{j=1}^n exp(\lambda_i f_i (y_{j-1}, y_j, \vec x, j)) \end{equation}

基于最大团上的函数连乘（(15)式所示）是线性链CRF通常所采用的表示方法。下文的讲述就是基于此种表示方法。

上面线性链CRF的最大团只有一个团模板(clique template) $C \in \mathcal C$，每个最大团的形式均为 $C=\lbrace \Psi_j (y_j, y_{j-1}, \vec x) | \forall j \in \lbrace1,2,...,n\rbrace \rbrace$，正因为有这样的线性链结构，我们可以用随机有限状态自动机（SFSA）来表示线性链CRF，这种状态自动机与隐马尔可夫模型类似，并且容易实现。其中，转移概率依赖于输入序列$\vec x$，比如上面那个线性链CRF的图，输入为向量$\vec x$，输出序列为$(y_1,y_2,...,y_n), y_i \in S$，其中S 表示状态集合。如下图是一个三状态$\lbrace S_1,S_2,S_3 \rbrace$自动机，

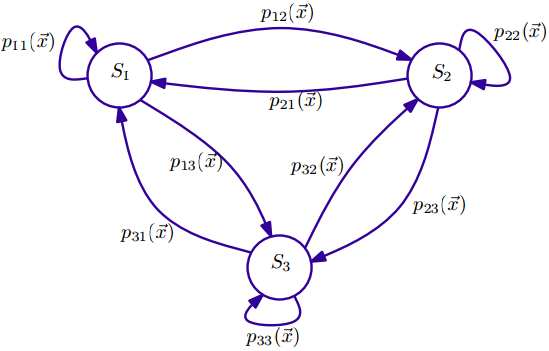
建立线性链CRF模型的策略总结如下：

1. 基于所有状态的集合S，以及转移矩阵$T=(s, \acute{s}) \in S^2)$，构造一个随机有限状态自动机SFSA $\mathcal S = (S, T)$，这个自动机可以完全连接，每个状态之间均有（有向）边连接，也可以根据实际情况禁止有些状态之间的连接（比如中文分词的B,M,E,S四个状态，B只与M和E有连接，与B和S没有连接等等）。
2. 对输入序列，指定特征模板集合$F={g_1 (\vec x, j),...,g_h (\vec x, j)}$，这些特征目标用于生成特征函数$f_i$。
3. 生成特征函数集合 $\mathcal {F} = \lbrace \forall s,  \acute{s} \in S. \forall g_o \in F : f_i (s, \acute{s}, g_o) \rbrace$

上面这个线性链CRF模型是一阶的。如果要定义高阶的线性链CRF，则特征函数的形式为，

$$f_i (\vec y, \vec x, j) = f_i(h_j (\vec y), \vec y, j) $$

$$ h_j (\vec y) = (y_{j-k}, ...,y_j) $$

其中k为阶数，对于高阶(k>1)，可以同样使用状态自动机，与上图不同的是，高阶情况的当前状态依赖于前面多个状态。

对这种特殊的线性链CRF，训练和预测的方法与HMM类似，即以下两个问题：

• 给定观测序列$\vec x$和CRF模型$\mathcal M$，如何发现最可能的分类序列$\vec y$？
• 给定分类序列集合$\mathcal Y$和观测 序列集合$\mathcal X$，如何进行CRF模型$\mathcal M$的参数估计，以使得对某一观测序列$\vec x$，其分类序列为$\vec y$的概率$p(\vec y | \vec x, \mathcal M)$最大？

问题1）是条件随机场常见的应用场景，即给观测序列进行分类得到分类序列。问题2）是关于训练的。关于这两个问题，我们下篇文章再详述。

ref

Classical Probabilistic Models and Conditional Random Fields