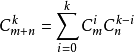Codeforces 785D Anton and School - 2 (范德蒙恒等式+ 乘法逆元)
As you probably know, Anton goes to school. One of the school subjects that Anton studies is Bracketology. On the Bracketology lessons students usually learn different sequences that consist of round brackets (characters "(" and ")" (without quotes)).
On the last lesson Anton learned about the regular simple bracket sequences (RSBS). A bracket sequence s of length n is an RSBS if the following conditions are met:
- It is not empty (that is n ≠ 0).
- The length of the sequence is even.
-
First
charactes
of the sequence are equal to "(". -
Last charactes
of the sequence are equal to ")".
For example, the sequence "((()))" is an RSBS but the sequences "((())" and "(()())" are not RSBS.
Elena Ivanovna, Anton's teacher, gave him the following task as a homework. Given a bracket sequence s. Find the number of its distinct subsequences such that they are RSBS. Note that a subsequence of s is a string that can be obtained from s by deleting some of its elements. Two subsequences are considered distinct if distinct sets of positions are deleted.
Because the answer can be very big and Anton's teacher doesn't like big numbers, she asks Anton to find the answer modulo 109 + 7.
Anton thought of this task for a very long time, but he still doesn't know how to solve it. Help Anton to solve this task and write a program that finds the answer for it!
The only line of the input contains a string s — the bracket sequence given in Anton's homework. The string consists only of characters "(" and ")" (without quotes). It's guaranteed that the string is not empty and its length doesn't exceed 200 000.
Output one number — the answer for the task modulo 109 + 7.
)(()()
6
()()()
7
)))
0
In the first sample the following subsequences are possible:
- If we delete characters at the positions 1 and 5 (numbering starts with one), we will get the subsequence "(())".
- If we delete characters at the positions 1, 2, 3 and 4, we will get the subsequence "()".
- If we delete characters at the positions 1, 2, 4 and 5, we will get the subsequence "()".
- If we delete characters at the positions 1, 2, 5 and 6, we will get the subsequence "()".
- If we delete characters at the positions 1, 3, 4 and 5, we will get the subsequence "()".
- If we delete characters at the positions 1, 3, 5 and 6, we will get the subsequence "()".
The rest of the subsequnces are not RSBS. So we got 6 distinct subsequences that are RSBS, so the answer is 6.
题解:
遇到右括号,记录, 遇到左括号 组合计算, 应用范德蒙式化简:
在 利用乘法逆元 计算组合数 :
AC代码:
#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <string>
#include <queue>
#include <stack>
#include <stdlib.h>
#include <list>
#include <map>
#include <set>
#include <bitset>
#include <vector>
#define mem(a,b) memset(a,b,sizeof(a))
#define findx(x) lower_bound(b+1,b+1+bn,x)-b
#define FIN freopen("input.txt","r",stdin)
#define FOUT freopen("output.txt","w",stdout)
#define S1(n) scanf("%d",&n)
#define S2(n,m) scanf("%d%d",&n,&m)
#define Pr(n) printf("%d\n",n)
using namespace std;
typedef long long ll;
const double PI=acos(-1);
const int INF=0x3f3f3f3f;
const double esp=1e-6;
const int maxn=1e6+5;
const int MOD=1e9+7;
const int mod=1e9+7;
int dir[5][2]={0,1,0,-1,1,0,-1,0};
ll inv[maxn*2],fac[maxn];
ll gcd(ll a,ll b){ return b?gcd(b,a%b):a;}
ll exgcd(ll a,ll b,ll &x,ll &y){if(!b){x=1;y=0;return a;}ll ans=exgcd(b,a%b,x,y);ll temp=x;x=y;y=temp-a/b*y;return ans;}
ll lcm(ll a,ll b){ return b/gcd(a,b)*a;}
ll qpow(ll x,ll n){ll res=1;for(;n;n>>=1){if(n&1)res=(res*x)%MOD;x=(x*x)%MOD;}return res;}
void INV(){inv[1] = 1;for(int i = 2; i < maxn; i++) inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD;}
void ex_gcd(ll a,ll b,ll &d,ll &x,ll &y){if(!b){ x=1; y=0; d=a; }else{ ex_gcd(b,a%b,d,y,x); y-=x*(a/b);}}
void Fac(){fac[0]=1;for(int i=1;i<=maxn;i++)fac[i]=(fac[i-1]*i)%MOD;}
ll inv_exgcd(ll a,ll n){ll d,x,y;ex_gcd(a,n,d,x,y);return d==1?(x+n)%n:-1;}
ll inv1(ll b){return b==1?1:(MOD-MOD/b)*inv1(MOD%b)%MOD;}
ll inv2(ll b){return qpow(b,MOD-2);}
ll cal(ll m,ll n){if(m<n)return 0;return (fac[m]*inv[fac[n]]%MOD)%MOD*inv[fac[m-n]]%MOD;}
ll cals(ll m,ll n){if(m<n)return 0;return (fac[m]*inv1(fac[n])%MOD)%MOD*inv1(fac[m-n])%MOD;}
char str[maxn];
int main()
{
Fac();
scanf("%s",&str);
int len=strlen(str);
int le=0,ri=0;
ll ans=0;
ll res=0;
for(int i=0;i<len;i++)
if(str[i]==')')
++ri;
for(int i=0;i<len;i++)
{
if(str[i]=='(')
{
++le;
ans=(ans+cals(le+ri-1,le))%mod;
}
else
ri--;
}
Pr(ans);
return 0;
}
/*
((((()(()))()))))))(()(
*/
