相机位姿估计0：基本原理之如何解PNP问题

关键词：相机位姿估计 PNP问题求解

用途：各种位姿估计

文章类型：原理

@Author：VShawn(singlex@foxmail.com)

@Date:2016-11-18

@Lab: CvLab202@CSU

 

目录

今天给大家讲一讲相机位姿估计的基本原理，说实话我本人也没太了解，这里权当做抛砖引玉了。本来我这个博客是写应用型文章的，但虽然不做理论研究，但你要使用别人的方法来解决问题，那么也还是多多少少要对它的原理有点了解的。

关于PNP问题就是指通过世界中的N个特征点与图像成像中的N个像点，计算出其投影关系，从而获得相机或物体位姿的问题。

 

以下讨论中设相机位于点Oc，P1、P2、P3……为特征点。

 

Case1：当N=1时

当只有一个特征点P1，我们假设它就在图像的正中央，那么显然向量OcP1就是相机坐标系中的Z轴，此事相机永远是面对P1，于是相机可能的位置就是在以P1为球心的球面上，再一个就是球的半径也无法确定，于是有无数个解。

Case2：当N=2时

现在多了一个约束条件，显然OcP1P2形成一个三角形，由于P1、P2两点位置确定，三角形的变P1P2确定，再加上向量OcP1，OcP2从Oc点射线特征点的方向角也能确定，于是能够计算出OcP1的长度=r1，OcP2的长度=r2。于是这种情况下得到两个球：以P1为球心，半径为r1的球A；以P2为球心，半径为r2的球B。显然，相机位于球A，球B的相交处，依旧是无数个解。

Case3：当N=3时

与上述相似，这次又多了一个以P3为球心的球C，相机这次位于ABC三个球面的相交处，终于不再是无数个解了，这次应该会有4个解，其中一个就是我们需要的真解了。

Case4：当N大于3时

N=3时求出4组解，好像再加一个点就能解决这个问题了，事实上也几乎如此。说几乎是因为还有其他一些特殊情况，这些特殊情况就不再讨论了。N>3后，能够求出正解了，但为了一个正解就又要多加一个球D显然不够"环保"，为了更快更节省计算机资源地解决问题，先用3个点计算出4组解获得四个旋转矩阵、平移矩阵。根据公式：

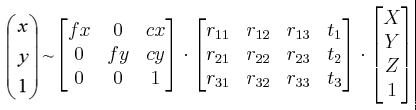
将第四个点的世界坐标代入公式，获得其在图像中的四个投影（一个解对应一个投影），取出其中投影误差最小的那个解，就是我们所需要的正解。

 

 

PNP问题的求解原理大致就是上面这样了，至于具体的数学方法还是请大家自己去查阅文献吧，本博客对这个问题的分析就到此为止了。接下来请看通过解PNP问题，求解相机位姿的应用。

posted @ 2016-11-20 17:00  V·Shawn  阅读(33222)  评论(5)  编辑  收藏  举报