网格弹簧质点系统模拟（Spring-Mass System by Verlet Integration）附源码

　　模拟物体变形最简单的方法就是采用弹簧质点系统（Spring-Mass System），由于模型简单并且实用，它已被广泛应用于服饰、毛发以及弹性固体的动态模拟。对于三角网格而言，弹簧质点系统将网格中的顶点看作系统中的质点，而网格的边则是连接这些质点的弹簧。这样，弹簧质点系统模型就将物体简化成由弹簧和质点组成的系统，并利用弹簧质点的运动规律来描述物体的弹性变形过程。

　　Verlet积分是求解牛顿运动方程的数值方法，原理简单描述如下：首先将系统t+dt时刻的位置x(t+dt)以及系统t-dt时刻的位置x(t-dt)用泰勒公式展开：

 

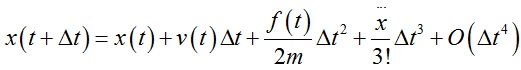
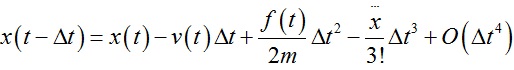
　　上面两式相加后得到：

 

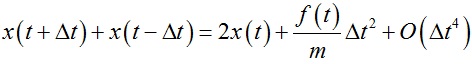
　　进一步变化得到：

 

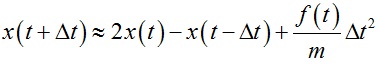
　　因此通过上式可以根据系统前两时刻的状态求解系统的当前状态，这与”基于网格的波动方程模拟“一文中的求解过程有些类似。

　　为了真实模拟物体变形效果，需要对弹簧质点系统进行受力分析：1. 每个质点有自身重力的影响；2. 每个质点受到与它相连的弹簧弹力影响，弹簧弹力遵守胡克定律；3. 质点运动时受到与其速度成正比的阻尼约束；4. 质点会受到其他外力的影响，由于施加的外力在每个三角面片上有一个法向分量，我们只需对每个质点周围三角片上的这些分量相加即可。

 

% constrains option
wind = false;
ball = true;
pins = false;

figure('Position', [400, 400, 400, 320]);
fh = drawMesh(V,F,'facecolor','y','edgecolor','none');
if ball
    center = [50 60 -80];
    radius = 40;
    drawSphere([center radius], 'facecolor','r', 'nPhi',96, 'nTheta',48);
end
if pins
    plot3([-10;110], [0;0], [0;0], 'k-', 'linewidth',2);
end
view([-30 20])
axis equal
axis off
axis([-10 100 -10 100 -110 0]);
camlight
lighting gouraud

set(gca, 'position', [0 0 1 1]);

% initial condition
x_pre = V;
x_cur = V;

% rest length
E = edges(F);
l0 = vectorNorm3d(V(E(:,1),:) - V(E(:,2),:)); 

nV = size(V,1);
draw_t = 0;
tic;
while true
    % spring force
    Fs = stiffness * (vectorNorm3d(x_cur(E(:,1),:) - x_cur(E(:,2),:)) - l0);
    dir = normalizeVector3d(x_cur(E(:,2),:) - x_cur(E(:,1),:));

    M1 = sparse(E, E, [Fs.*dir(:,1);-Fs.*dir(:,1)]);
    M2 = sparse(E, E, [Fs.*dir(:,2);-Fs.*dir(:,2)]);
    M3 = sparse(E, E, [Fs.*dir(:,3);-Fs.*dir(:,3)]);
    as = [diag(M1), diag(M2), diag(M3)] ./ m;

    % wind force
    aw = zeros(nV,3);
    if wind
        N = normalizeVector3d(normals(x_cur,F));
        Fw = N * wind_force(i/10)' .* wind_strength;

        M1 = sparse(F, F, repmat(Fw.*N(:,1),1,3));
        M2 = sparse(F, F, repmat(Fw.*N(:,2),1,3));
        M3 = sparse(F, F, repmat(Fw.*N(:,3),1,3));
        aw = [diag(M1), diag(M2), diag(M3)] ./ m;
    end

    % verlet integration with a simple damping model
    x_new = drag*(x_cur - x_pre) + x_cur + bsxfun(@plus, as+aw, g)*dt*dt;

    x_pre = x_cur;
    x_cur = x_new;

    % ball constrains
    if ball
        diff = bsxfun(@minus, x_cur, center);
        index = vectorNorm3d(diff) < radius+1;
        x_cur(index,:) = bsxfun(@plus, center, bsxfun(@times, normalizeVector3d(diff(index,:)), radius+1));
    end

    % pin constrains
    if pins
        x_pre(pin_idx,:) = V(pin_idx,:);
        x_cur(pin_idx,:) = V(pin_idx,:);
    end

    % updata figure
    if toc > 0.033
        set(fh, 'Vertices', x_cur);
        drawnow;
        tic;
    end
end

本文为原创，转载请注明出处：http://www.cnblogs.com/shushen。