Clustering[Evaluation]

---

0. 背景

评估（或者说验证）聚类结果就如同聚类本身一样困难。通常的方法有内部评估和外部评估这两种：

• 内部评估的方法：通过一个单一的量化得分来评估算法好坏；该类型的方法
• 外部评估的方法：通过将聚类结果与已经有“ground truth”分类进行对比。要么通过人类进行手动评估，要么通过一些指标在特定的应用场景中进行聚类用法的评估。不过该方法是有问题的，如果真的有了label，那么还需要聚类干嘛，而且实际应用中，往往都没label；另一方面，这些label只反映了数据集的一个可能的划分方法，它并不能告诉你存在一个不同的更好的聚类算法。

上述的方法还是不能最优判决聚类真正的效果，还是需要人类的参与，这是一个相当主观的事情。然而，这样的统计方法可以验证那些相当不好的聚类结果。不过仍然需要尊重人类的评价结果。

1. 内部评估的方法

当一个聚类结果是基于数据聚类自身进行评估的，这一类叫做内部评估方法。如果某个聚类算法聚类的结果是类间相似性低，类内相似性高，那么内部评估方法会给予较高的分数评价。不过内部评价方法的缺点是：

• 那些高分的算法不一定可以适用于高效的信息检索应用场景；
• 这些评估方法对某些算法有倾向性，如k-means聚类都是基于点之间的距离进行优化的，而那些基于距离的内部评估方法就会过度的赞誉这些生成的聚类结果。

这些内部评估方法可以基于特定场景判定一个算法要优于另一个，不过这并不表示前一个算法得到的结果比后一个结果更有意义。这里的意义是假设这种结构事实上存在于数据集中的，如果一个数据集包含了完全不同的数据结构，或者采用的评价方法完全和算法不搭，比如k-means只能用于凸集数据集上，许多评估指标也是预先假设凸集数据集。在一个非凸数据集上不论是使用k-means还是使用假设凸集的评价方法，都是徒劳的。

Davies-Bouldin 指标

该指标的计算公式：

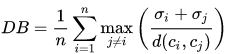
其中n是类别个数，\(c_x\)是第\(x\)个类别的中心，\(\sigma_x\)是类别\(x\)中所有的点到中心的平均距离；\(d(c_i,c_j)\)是中心点\(c_i\)和\(c_j\)之间的距离。算法生成的聚类结果越是朝着类内距离最小（类内相似性最大）和类间距离最大（类间相似性最小）变化，那么Davies-Bouldin指数就会越小。

Dunn 指标

该指标意在，衡量密度和很好划分的聚类数据集。

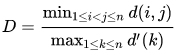
其中\(d(i,j)\)表示类别\(i.j\)之间的距离；\(d'(k)\)表示类别\(k\)内部的类内距离：

• 类间距离\(d(i,j)\)可以是任意的距离测度，例如两个类别的中心点的距离；
• 相似的，类内距离\(d'(k)\)可以以不同的方法去测量，例如类别\(k\)中任意两点之间距离的最大值。

因为内部评估方法是搜寻类内相似最大，类间相似最小，所以算法生成的聚类结果的Dunn指数越高，那么该算法就越好。

Silhouette 系数

该指数是通过将到同一个类别中其他点的平均距离和到其他类别中其他点的平均距离进行对比。该值越高，就认为该点被聚类的越好，该值如果很低，那么这些点可能就是离群点。该指数可以很好的适用k-means，通常用来决定最优的类别个数k是多少。

2. 外部评估方法

在外部评估方法中，聚类结果是通过使用没被用来做训练集的数据进行评估。例如已知样本点的类别信息和一些外部的基准。这些基准包含了一些预先分类好的数据，比如由人基于某些场景先生成一些带label的数据，因此这些基准可以看成是金标准。这些评估方法是为了测量聚类结果与提供的基准数据之间的相似性。然而这种方法也被质疑不适用真实数据。

Purity
该方法是用来评估聚类后每个类别包含单个样本类别的程度。计算原理：对于每个聚类类别，统计最多归属类别的样本个数的比例。：

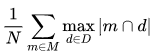
举个例子：

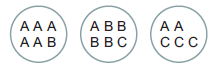
图2.1 样例
如图，一共17个样本点，其中字母表示样本点归属的label。而三个圆圈表示聚类之后的结果。
如公式，计算得\(\frac{1}{17}\left[ 5+4+3 \right]\)。表示三个圈中的最大归属类别的纯度
该方法的缺点是不关心到底有多少个聚类的类别，如果每个样本点自己成为一个类别，那么该方法的值将达到1.

Rand 测度
该方法计算聚类结果与基准分类之间的相似性：

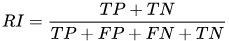
举个例子，用图2.1的数据,该方法是基于两个样本点，即样本对来进行计算得：
TP表示相同label在同一个聚类类别中计算得\(TP=C_5^2+C_4^2+[C_3^2+C_2^2]=20\);
TP+FP表示样本被预测为正的结果\(TP+FP=C_6^2+C_6^2+C_5^2=40\);\(FP=40-20=20\);
FN表示相同label在不同聚类类别中\(FN=[C_5^1C_1^1]_{A_{12}}+[C_5^1C_2^1]_{A_{13}}+[C_1^1C_2^1]_{A_{23}}+[C_1^1C_4^1]_{B_{12}}+[C_1^1C_3^1]_{C_{23}}=24\)
TN表示不同label在不同聚类类别中\(TN=[C_5^1C_4^1]_{A_1B_2}+[C_5^1C_1^1]_{A_1C_2}+[C_5^1C_3^1]_{A_1C_3}+[C_1^1C_1^1]_{B_1A_2}+[C_1^1C_1^1]_{B_1C_2}+[C_1^1C_2^1]_{B_1A_3}+[C_1^1C_3^1]_{B_1C_3}+[C_1^1C_3^1]_{A_2C_3}+[C_4^1C_2^1]+{B_2A_3}+[C_4^1C_3^1]_{B_2C_3}+[C_1^1C_2^1]_{C_2A_3}=72\)
最后得结果\(\frac{20+72}{20+20+24+72}=0.68\)
该方法的缺点是假阳性和假阴性的权重是一样的，对于许多场景来说，这个特性可能并不好。该方法当\(TP=TN=0\)时得到结果0

F-测度
该方法可以通过引入一个变量来平衡假阴性。先计算准确率和召回率

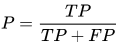
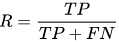
这里P就是准确率，R就是召回率，F测度公式为：

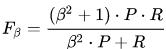
当\(\beta=0\)时，就是准确率，这时候召回率的影响为0，通过增加\(\beta\)可以调节两个值的影响程度

Jaccard 指数
该指数用于量化两个数据集之间的相似性，该值得范围为0-1.其中越大表明两个数据集越相似：

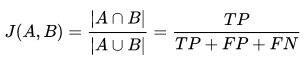
该指数和近年来的IOU计算方法一致

Dice 指数
该指数是基于jaccard指数上将TP的权重置为2倍。

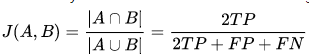
Fowlkes-Mallows 指数
该指数计算聚类算法返回的数据集和基准分类之间的相似性。值越高表示越相似：

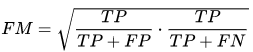
该指数表示准确率和召回率的几何平均数，因此也被称为G-测度（F-测度被称为harmonic平均数）。

mutual information
互信息是信息论的测度方式，用于计算两个数据集之间的信息共享程度，同时也可以用来测量两个数据集之间的非线性相似性。
\(p_{UV}(i,j)=\frac{|u_i\cap v_j|}{N}\)表示一个样本点属于\(U\)中\(u_i\)类别和\(V\)中\(v_j\)类别的概率。同样的，\(p_U(i)=\frac{u_i}{N}\)表示一个样本点属于\(U\)中\(u_i\)类别的概率，\(p_V(j)=\frac{v_j}{N}\)类似。其中\(N\)表示数据集中样本点个数。

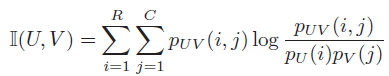
该指数值介于0和\(\left\{H(U),H(V)\right\}\)之间。不过不幸的是，最大值可以通过使用许多小聚类来达到，这时候熵会很低（每个样本自成一类），为了克服这个问题，可以使用归一化的互信息：

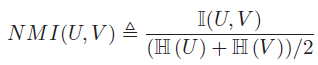
该指数值介于0-1之间。
其中

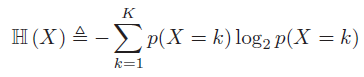
K表示类别个数，\(p(X = k)\)表示一个样本属于类别k的概率

混淆矩阵
混淆矩阵可以快速的可视化结果。这个在分类领域也用的相当多

3. 聚类趋势

测量聚类趋势是为了测量数据集中聚类的可能性。可以用作聚类之前的一个测试。其中的一种方法就是对比数据集和随机数据，因为理论上来说，随机数据是不能被聚类的。
Hopkins statistic
有多个式子来实现Hopkins统计。其中较为典型的是：

• 让\(X\)表示在\(d\)维空间上的\(n\)个数据点，先对其随机采样\(m\ll n\)个数据点\(x_i\)。同时随机生成\(m\)个均匀分布的数据点集合\(Y\)。现在定义两个距离测度：

• \(u_i\)表示\(y_i\in Y\)到\(X\)中最近的点的距离；
• \(w_i\)表示\(x_i\in X\)到\(X\)中最近的点的距离。
  然后计算：
  
  通过这个定义，均匀采样的数据通常倾向得到值为0.5，而可以聚类的数据可以得到接近1的值。然而当数据值包含一个高斯分布的时候，同样也能得到值1，因为该统计是测量偏离均匀分布的程度，而不是呈现多模态的特性，从而使得该统计量在实际应用中基本没用（因为真实数据从来都不是均匀分布的）。

参考文献：
[1] - Machine learning, a probabilistic perspective
[2] - .Evaluation_and_assessment