Generative Adversarial Nets[Vanilla]
引言中已经较为详细的介绍了GAN的理论基础和模型本身的原理。这里主要是研读Goodfellow的第一篇GAN论文。
0. 对抗网络
如引言中所述,对抗网络其实就是一个零和游戏中的2人最小最大游戏,主要就是为了处理下面的函数\(V(G,D)\):
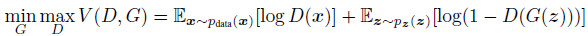
在实现过程中,如果将D和G都写入同一个循环中,即迭代一次D,迭代一次G,这种情况会让在有限的数据集基础上会导致过拟合。所以Goodfellow推荐:先训练D模型K步,然后再训练G一步。这样可以让D很好的接近最优解,并且让G改变的足够慢。

图0.1 GAN的训练流程伪代码
1. 理论结果
1.1 \(p_g=p_{data}\)的全局优化
首先,我们讨论下基于任何给定的生成器G的基础上,最优的判决器D。
[待续]
1.2 算法的收敛
[待续]
2. 实验结果
[待续]
3. 优缺点
[待续]
4.示例代码解析
此部分主要参考自github。这里主要涉及到4个点:
- 1 - 读取mnist的数据;
- 2 - 构建一个判别器网络;
- 3 - 构建一个生成器网络;
- 4 - 基于SGD,采用联合更新的方式来训练这两个网络从而完成生成对抗网络的训练。
4.1 载入前置模块及mnist数据
import tensorflow as tf
import random
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/")#手动下载mnist的4个gz压缩包,放入当前路径的MNIST_data文件夹下面
4.2 构建判别器网络
基于CNN网络结构,构建一个判别器,用于输出当前输入的图片为real data的概率值。
#先定义卷积和平均池化的函数,这2个就是常见的CNN的卷积和池化操作
def conv2d(x, W):
#input:[batch, in_height, in_width, in_channels]
#filter:[filter_height, filter_width, in_channels, out_channels]
return tf.nn.conv2d(input=x, filter=W, strides=[1, 1, 1, 1], padding='SAME')
def avg_pool_2x2(x):
return tf.nn.avg_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
因卷积和池化操作会多次用到,所以先建立成函数,下面构建判别器网络结构
def discriminator(x_image, reuse=False):
with tf.variable_scope('discriminator') as scope:
if reuse:
tf.get_variable_scope().reuse_variables()
'''第一层:卷积层和池化层,该层的激活函数为ReLU'''
#结构为:conv->ReLU->avgPool
#卷积层感受野大小5x5,输入channel(或者叫做depth)为1,输出channel为8; 输出的feature map为14*14*8
W_conv1 = tf.get_variable('d_wconv1', [5, 5, 1, 8], initializer=tf.truncated_normal_initializer(stddev=0.02))
b_conv1 = tf.get_variable('d_bconv1', [8], initializer=tf.constant_initializer(0))
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = avg_pool_2x2(h_conv1)
'''第二层:卷积层和池化层,其他如第一层所述; '''
#输出的feature map为7*7*16
W_conv2 = tf.get_variable('d_wconv2', [5, 5, 8, 16], initializer=tf.truncated_normal_initializer(stddev=0.02))
b_conv2 = tf.get_variable('d_bconv2', [16], initializer=tf.constant_initializer(0))
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = avg_pool_2x2(h_conv2)
'''第三层:一个全连接层,输入维度7*7*16,输出维度32'''
W_fc1 = tf.get_variable('d_wfc1', [7 * 7 * 16, 32], initializer=tf.truncated_normal_initializer(stddev=0.02))
b_fc1 = tf.get_variable('d_bfc1', [32], initializer=tf.constant_initializer(0))
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*16])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
'''第四层:一个全连接层,输入维度32,输出维度1,用于判别当前输入图片属于real data的概率,此处无激活函数'''
W_fc2 = tf.get_variable('d_wfc2', [32, 1], initializer=tf.truncated_normal_initializer(stddev=0.02))
b_fc2 = tf.get_variable('d_bfc2', [1], initializer=tf.constant_initializer(0))
y_conv=(tf.matmul(h_fc1, W_fc2) + b_fc2)
return y_conv
4.3 构建生成器网络
CNN可以被看成是输入一个2维矩阵或者3维的张量,输出一个单一的概率值;而生成器,就是输入一个d维的噪音向量,上采样成一个2维的矩阵或者3维的张量。
def generator(z, batch_size, z_dim, reuse=False):
#z:输入的噪音向量
with tf.variable_scope('generator') as scope:
if reuse:
tf.get_variable_scope().reuse_variables()
g_dim = 64 #生成器第一层的channel个数
c_dim = 1 #输出的颜色空间维度 (MNIST 是灰度图片,所以 c_dim = 1)
s = 28 #图片的输出尺寸
s2, s4, s8, s16 = int(s/2), int(s/4), int(s/8), int(s/16) #为了缓慢的上采样,变化尽可能的小。分别为14,7,3,2
'''输入z是基于随机采样生成的,即噪音输入'''
#h0 的维度:[ batch_size, 2, 2, 25],所以z的维度为[batch_size, 100]
h0 = tf.reshape(z, [batch_size, s16+1, s16+1, 25])
h0 = tf.nn.relu(h0)
'''第一个解卷积层,采用conv2d_transpose实现'''
#先定义权重和偏置,
#H_conv1的维度:[batch_size, 3, 3, 256]
output1_shape = [batch_size, s8, s8, g_dim*4]#[batch_size,3,3,64]
W_conv1 = tf.get_variable('g_wconv1', [5, 5, output1_shape[-1], int(h0.get_shape()[-1])],
initializer=tf.truncated_normal_initializer(stddev=0.1))
#b_conv1 = tf.get_variable('g_bconv1', [output1_shape[-1]], initializer=tf.constant_initializer(.1))
#采用conv2d_transpose实现解卷积,并加上BN,ReLU
#conv2d_transpose:
# 参数1 input(h0) - [batch, height, width, in_channels]或者batch, in_channels, height, width]
# 参数2 filter(W_conv1) - [height, width, output_channels, in_channels]
H_conv1 = tf.nn.conv2d_transpose(h0, W_conv1, output_shape=output1_shape, strides=[1, 2, 2, 1], padding='SAME')
#H_conv1 = tf.reshape(tf.nn.bias_add(H_conv1, b_conv1), H_conv1.get_shape())
H_conv1 = tf.contrib.layers.batch_norm(inputs = H_conv1, center=True, scale=True, is_training=True, scope="g_bn1")
H_conv1 = tf.nn.relu(H_conv1)
'''第二个解卷积层'''
#H_conv2的维度:[batch_size, 6, 6, 128]
output2_shape = [batch_size, s4 - 1, s4 - 1, g_dim*2]
W_conv2 = tf.get_variable('g_wconv2', [5, 5, output2_shape[-1], int(H_conv1.get_shape()[-1])],
initializer=tf.truncated_normal_initializer(stddev=0.1))
#b_conv2 = tf.get_variable('g_bconv2', [output2_shape[-1]], initializer=tf.constant_initializer(.1))
H_conv2 = tf.nn.conv2d_transpose(H_conv1, W_conv2, output_shape=output2_shape, strides=[1, 2, 2, 1], padding='SAME')
#H_conv2 = tf.reshape(tf.nn.bias_add(H_conv2, b_conv2), H_conv2.get_shape())
H_conv2 = tf.contrib.layers.batch_norm(inputs = H_conv2, center=True, scale=True, is_training=True, scope="g_bn2")
H_conv2 = tf.nn.relu(H_conv2)
'''第三个解卷积层'''
#H_conv3的维度:[batch_size, 12, 12, 64]
output3_shape = [batch_size, s2 - 2, s2 - 2, g_dim*1]
W_conv3 = tf.get_variable('g_wconv3', [5, 5, output3_shape[-1], int(H_conv2.get_shape()[-1])],
initializer=tf.truncated_normal_initializer(stddev=0.1))
#b_conv3 = tf.get_variable('g_bconv3', [output3_shape[-1]], initializer=tf.constant_initializer(.1))
H_conv3 = tf.nn.conv2d_transpose(H_conv2, W_conv3, output_shape=output3_shape, strides=[1, 2, 2, 1], padding='SAME')
#H_conv3 = tf.reshape(tf.nn.bias_add(H_conv3, b_conv3 ), H_conv3.get_shape())
H_conv3 = tf.contrib.layers.batch_norm(inputs = H_conv3, center=True, scale=True, is_training=True, scope="g_bn3")
H_conv3 = tf.nn.relu(H_conv3)
'''第四个解卷积层'''
#H_conv4的维度:[batch_size, 28, 28, 1]
output4_shape = [batch_size, s, s, c_dim]
W_conv4 = tf.get_variable('g_wconv4', [5, 5, output4_shape[-1], int(H_conv3.get_shape()[-1])],
initializer=tf.truncated_normal_initializer(stddev=0.1))
#b_conv4 = tf.get_variable('g_bconv4', [output4_shape[-1]], initializer=tf.constant_initializer(.1))
H_conv4 = tf.nn.conv2d_transpose(H_conv3, W_conv4, output_shape=output4_shape, strides=[1, 2, 2, 1], padding='VALID')
#H_conv4 = tf.reshape(tf.nn.bias_add(H_conv4, b_conv4), H_conv4.get_shape())
H_conv4 = tf.nn.tanh(H_conv4)
return H_conv4
4.4 联合训练
联合训练判别器和生成器
batch_size = 16
z_dimensions = 100
tf.reset_default_graph() #
sess = tf.Session()
'''设定real data和噪音的占位数据 '''
x_placeholder = tf.placeholder("float", shape = [None,28,28,1]) #real data的输入
z_placeholder = tf.placeholder(tf.float32, [None, z_dimensions]) #输入到生成器中的噪音
'''基于编写好的判别器和生成器建立关系 '''
Dx = discriminator(x_placeholder) #判别器,对real data的判别概率(unnormalized)
Gz = generator(z_placeholder, batch_size, z_dimensions) #生成器,基于噪音数据,生成伪造数据
Dg = discriminator(Gz, reuse=True) #判别器,对生成器生成的伪造图片的判别概率 (unnormalized)
'''生成器的loss定义 '''
#'''对伪造图片判别结果的loss值: <判别结果, 期望其为1>之间的交叉熵值 '''
g_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=Dg, labels=tf.ones_like(Dg)))
'''判别器的loss定义 '''
#'''对真实图片判别结果的loss值: <判别结果,本身为1>之间的交叉熵值 '''
d_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=Dx, labels=tf.ones_like(Dx)))
#'''对伪造图片判别结果loss值: <判别结果,本身为0>之间的交叉熵值 '''
d_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=Dg, labels=tf.zeros_like(Dg)))
#上述两个loss值相加
d_loss = d_loss_real + d_loss_fake
'''从graph中提取所有可以训练的变量,并区分出判别器的变量和生成器的变量 '''
tvars = tf.trainable_variables()
d_vars = [var for var in tvars if 'd_' in var.name]
g_vars = [var for var in tvars if 'g_' in var.name]
'''调用SGD进行判别器和生成器loss的迭代训练 '''
with tf.variable_scope(tf.get_variable_scope(), reuse=False):
trainerD = tf.train.AdamOptimizer().minimize(d_loss, var_list=d_vars)
trainerG = tf.train.AdamOptimizer().minimize(g_loss, var_list=g_vars)
sess.run(tf.global_variables_initializer())
iterations = 3000
for i in range(iterations):
'''生成噪音数据和读取真实数据 '''
z_batch = np.random.normal(-1, 1, size=[batch_size, z_dimensions])#生成噪音数据
real_image_batch = mnist.train.next_batch(batch_size)#提取真实图片的minibatch并进行reshape
real_image_batch = np.reshape(real_image_batch[0],[batch_size,28,28,1])
'''训练判别器,生成器 '''
_,dLoss = sess.run([trainerD, d_loss],feed_dict={z_placeholder:z_batch,x_placeholder:real_image_batch}) #判别器
_,gLoss = sess.run([trainerG,g_loss],feed_dict={z_placeholder:z_batch}) #生成器
'''训练结束之后,利用训练好的生成器,生成图片 '''
sample_image = generator(z_placeholder, 1, z_dimensions, reuse=True)
z_batch = np.random.normal(-1, 1, size=[1, z_dimensions])
temp = (sess.run(sample_image, feed_dict={z_placeholder: z_batch}))
my_i = temp.squeeze()
plt.imshow(my_i, cmap='gray_r')
生成图片

PS:GAN是很难训练的,其需要【正确的超参数,网络结构,训练流程】,否则会有很大几率生成器或者判别器会超过另一个。比如:
- 生成器找到了判别器的一个漏洞,从而重复的输出可以欺骗判别器的图片,但是图片本身却并不具有可视性(比如对抗样本);
- 生成器陷入单点上,因而无法输出多样化的数据,即总是输出同一类同一张图片;
- 判别器太厉害了,以至于怎么训练都被区分出真假。(一个方法是生成器学习率大于判别器,不过不一定有效)
这些现象背后的直观数学解释是:在实际实现GAN中,是采用梯度下降的方式寻找cost函数的最小值,而不是真的实现零和游戏的纳什平衡。当真的采用纳什平衡时,这些算法都是无法收敛的。所以需要研究出稳定的优化算法从而能够如训练CNN一样训练GAN。
在原始论文中,生成器和判别器的loss如下:
log = lambda x: tf.log(x + 1e-7)
'''生成器的loss:最大化log(D(G(z)))'''
g_loss = -tf.reduce_mean(log(Dg))
'''判别器的loss:最大化log(D(x)) + log(1 - D(G(z)))'''
d_loss = -tf.reduce_mean(log(Dx) + log(1. - Dg))
如果采用上述原文loss,记得在def discriminator(x_image, reuse=False)的输出部分加上:
y_conv = tf.nn.sigmoid(y_conv)
参考资料:
[] - .tutorial




