Feature Extractor[ResNet v2]
0. 背景
何凯明大神等人在提出了ResNet网络结构之后,对其做了进一步的分析工作,详细的分析了ResNet 构建块能起作用的本质所在。并通过一系列的实验来验证恒等映射的重要性,并由此提出了新的构建块模型使得网络能够更容易训练和更好的泛化性能(比如不同于ResNet v1中对cifar-10的学习率的谨慎,这里更加放开了)。
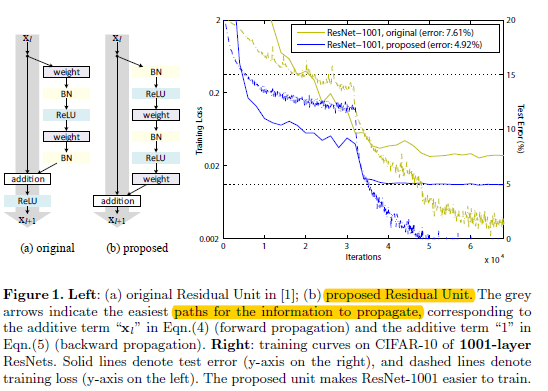
图0.1 v1中的残差构建块和v2中建议的残差构建块
如图0.1所示,在ResNet v1中,构建块是通过将之前层的\(x\)连接到后面跳过至少2层的输出,然后将和放入激活函数,如公式:
这其中\(x_l\)和\(x_{l+1}\)分别是第\(l\)层和第\(l+1\)层的输入。在V1中,\(h(x_l)=x_l\)就是一个恒等映射,\(f\)是ReLU激活函数,且ResNet的中心思想就是为了学习关于\(h(x_l)\)的附加残差函数\(f\)(\(h(x)=f(x)+x\)),这其中假设了恒等映射函数\(h(x_l)=x_l\)是最优函数,并且通过简单的快捷连接轻松实现了该想法。虽然ResNet效果很赞,不过在网络超过1k层的时候,还是会有略微的过拟合等情况,而且对ResNet为什么如此巨大成功,仍需要进行更多的想法验证。
ps:图0.1中左边的b子图是将权重层放在激活函数后面,而不是传统的先权重层,然后再过激活函数。这样设计之后的实验结果表明,网络更容易训练,而且泛化性能更好,之前在imagenet上v1网络超过200层就开始过拟合了,而在这里的v2就能很好的解决这个问题了。
在V2中,作者主要关注的不是残差单元,而是如何构建一个能够直接通达整个网络的信息传输路径,并通过试验发现,如果\(h(x)\)和\(f(x)\)都是恒等映射,那么信号可以不论是前馈还是反馈方向,能够直接从一个单元传递到任何其他单元。并且为了理解跳跃连接(即快捷连接)所存在的意义,作者分析了多个不同的\(h(x)\)形式,并发现当\(h(x)=x\)的时候(即图0.1的proposed),网络训练的时间最少,而且训练loss最低。这些实验也表明保持一个“干净的信息路径”有助于模型的优化。
1. 深度残差模型的分析
对于图0.1中的original模块,我们可以有如下的式子:
$ y_l=h(x_l)+F(x_l,W_l) $ (1)
$ x_{l+1}=f(y_l) $ (2)
也就是\(h(x_l)\)是图中的灰色大粗箭头,而\(F(x_l,W_l)\)就是边上的残差模块,这样角度的解释相对Resnet v1中到时更直观了,我们可以看出,如果以这样的形式叠加下去,那么左边永远是一个大粗线,右边在不断的添加模块,像是分支道路依附于左边的主干道路一样。其中\(f\)函数是一个逐元素相加的操作,且激活函数选得是ReLU。这其中\(h(x)\)选得是恒等映射,即\(h(x)=x\)
如果,我们假设\(f(x)=x\),也就是\(x_{l+1}=y_l\),那么将式子(2)带入(1)中,得到如下形式:
$ x_{l+1}=x_l+F(x_l,W_l) $ (3)
将其不断的展开:\((x_{l+2}=x_{l+1}+F(x_{l+1},W_{l+1}))=x_l+F(x_l,W_l)+F(x_{l+1},W_{l+1})\)
从而:
$x_L=x_l+\sum_{i=l}^{L-1}F(x_i,W_i) $ (4)
这个公式可以用来表示任何深度的残差网络,从中我们可以看到它有这么几个特性:
- 任何深度的层的特征\(x_L\)可以表示成某一层初始层\(x_l\)加上他们之间的残差的和,也就是该模型就是为了学到层\(L\)与层\(l\)之间的残差,
- 而且我们可以认为\(x_L=x_0+\sum_{i=0}^{L-1}F(x_i,W_i)\) 其表示的意思是:模型的输出等于模型的输入加上他们之间的残差,相比于传统的神经网络是一系列矩阵向量的相乘,而这里是相加操作。
从反向传播来看,假设损失函数为\(\large\varepsilon\),则链式求导如下:
\(\frac{\partial \large\varepsilon}{\partial x_l}=\frac{\partial \large\varepsilon}{\partial x_L}\frac{\partial x_L}{\partial x_l}=\frac{\partial \large\varepsilon}{\partial x_l}\left(1+\frac{\partial}{\partial x_l}\sum_{i=l}^{L-1}F(x_i,W_i)\right)\) (5)
从式子5中可以看出梯度\(\frac{\partial \large\varepsilon}{\partial x_l}\)可以分解成2个项相加:
- \(\frac{\partial}{\partial x_L}\)表示没有任何层阻挡的信息直接的传输;
- \(\frac{\partial \large\varepsilon}{\partial x_L}\left(\frac{\partial}{\partial x_l}\sum_{i=l}^{L-1}F\right)\)表示经过网络层的信息传输
上面第一项可以保证信息是直接从高层传递到低层的,而且他也不太可能会在一个mini-batch中被抵消掉,因为在一个mini-batch中不是所有的样本的\(\frac{\partial }{\partial x_l}\sum_{i=l}^{L-1}F\)都等于-1。这也表示了一层网络的梯度即使在权重值十分小的时候也不会发生梯度消失的问题
上述式子(4)(5)也表示了信息可以直接从某一个单元直接传递到任何其他的单元,不论是前向还是反向。不过值得注意的是,这里的式子(4)是基于2个前提的:
- 快捷连接是恒等映射\(h(x_l)=x_l\);
- 最后的激活函数也是恒等映射\(f(x_{l+1})=x_{l+1}\)
同时满足上面两个条件的模型,被称之为"干净"的模型。
2. 恒等快捷连接的重要性
在看到论文这部分之前,我也有个疑问,为什么一定是恒等映射,而不能是更复杂一些的仿射映射或者说非线性映射?然后就被本小节教做人了。本小节主要讨论恒等映射的重要性,所以仍然假设\(f(x_l)=x_l\)。
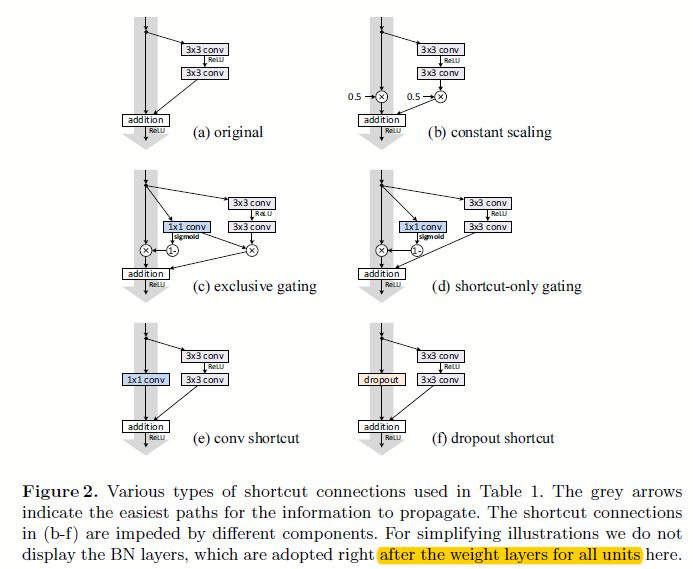
图2.1 基于不同设定的映射下的构建块结构
这里我们分成仿射映射和非线性映射:
- 对图图2.1中灰色大粗线部分进行信息的拦截,如乘以0.5,或者通过如lstm里面的门的概念一样以另一个子网络来计算出当前每个神经元的信息过滤程度;
- 不同于上面简单的乘以某个值进行缩放,这里引入如\(1*1\),dropout等非线性的信息拦截方式
为什么不能进行仿射映射和非线性拦截呢?
\(x_{l=1}=\lambda_lx_l+F(x_l,W_l)\)
如上面式子,其中\(\lambda_l\)就是一个缩放因子,我们通过如式子(4)进行展开:
\(x_L=(\prod_{i=l}^{L-1}\lambda_i)x_i+\sum_{i=l}^{L-1}\left(\prod_{j=i+i}^{L-1}\lambda_j\right)F(x_i,W_i)\)
简化之后:
\(x_L=\left(\prod_{i=l}^{L-1}\lambda_i\right)x_l+\sum_{i=l}^{L-1}\hat F(x_i,W_i)\)
这里\(\hat F\)表示其中比之前的\(F\)包含了缩放因子。
再如式子(5)进行求其链式导数:
\(\frac{\partial \large\varepsilon}{\partial x_l}=\frac{\partial \large\varepsilon}{\partial x_l}\left(\left(\prod_{i=l}^{L-1}\lambda_i\right)+\frac{\partial}{\partial x_l}\sum_{i=l}^{L-1}\hat F(x_i,W_i)\right)\)
从上面式子可以看出,如果当\(\lambda_i\)选取不同范围的时候:
- 大于1时,会随着网络的深度呈指数放大;
- 小于1时,会随着网络的深度呈指数缩小,然后消失。这样可以看成是该通道(构建块中的灰色大粗箭头)阻碍了信息的传输,使得强迫信息走右边的分支道路,即网络权重层。
从上面分析可以看出,不论是大于1还是小于1,都会给模型的优化带来困难。所以对于如图2.1中\(1*1\)卷积等非线性拦截模式来说,就更困难了。
基于实验可以分析出图2.1中不同设定下模型的结果:

图2.2 基于不同设定的映射下的结果对比
如上图所示,还是当恒等映射的时候效果最好。且事实上门和\(1*1\)的卷积(即仿射映射和非线性映射)已经覆盖到了恒等映射的解空间了,然而他们的训练误差却比恒等映射要高,这就表示了模型的“退化现象”不是因为表征能力的问题,而是因为优化不对导致的。
3. 激活函数的使用
ps:一个瓶颈式残差单元由一个\(1*1\)卷积(负责降维),一个\(3*3\)卷积,一个\(1*1\)卷积(负责升维)组成。它的计算复杂度和一个由2层\(3*3\)组成的残差单元相当。
这部分中,主要研究不同的位置排布对模型的影响,其中主要有这么几个排布:
- 将BN层放在相加之后;
- 将ReLU激活函数放在相加之前;
- 将ReLU激活函数统一放到权重层之前;
- 将BN放到ReLU激活函数之前,将ReLU放到权重层之前。
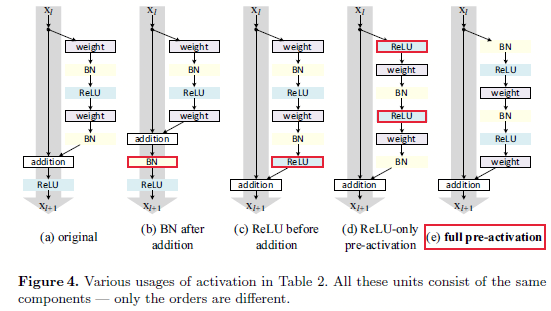
图3.1 不同的激活函数位置排布
如图3.1所示,作者设计了这么几个不同的排布位置,其中当
- 1 - BN放在加操作之后:不同于最开始的设计,这样设计使得BN修改了通过快捷连接的信号并且阻碍了信息的传输,在训练开始会收到训练loss减少困难的影响。
- 2 - ReLU放在加操作之前:如果我们想要让\(f\)变成恒等映射,那么最简单的想法就是将ReLU放在加操作之前,如图3.1的c。然而这样会导致函数\(F\)的输出永远是非负的,而我们也认为残差么,肯定有正有负,如果只有正的,那肯定是不正常的,因为参数空间直接砍了一大块。
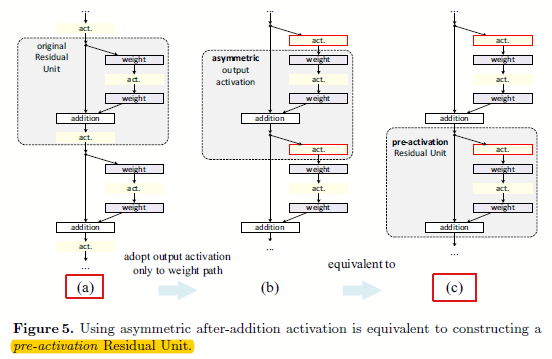
图3.2 基于非对称的后加(after-addition)修改,等于构建一个预先激活(pre-activation)的残差单元
从图3.2可以看出,既然不能naive的将ReLU放在加操作前,那么就直接将ReLU放在分支道路上,也就是残差通道部分,如图3.2的b。其中图3.2(b)相比3.2(a)就是简单的将ReLU移动到分支上了。然后通过另一个角度观察,其实这时候的网络结构就相当于预先激活。
是后激活还是先激活,主要是因为逐元素相加这个部分考虑的。对于一个传统的有N层的网络来说,将其放在后面还是前面,其实没什么影响,可是对于残差网络的分支(即非灰色大粗箭头部分)就有影响了。

图3.2 不同排布下的结果
如图3.2所示,预先激活的好处有2:
- 更容易训练:通过实验发现在1001层上结果对比特别明显,v1版本的残差单元的训练误差下降非常慢;因为\(f\)的ReLU信号受到了负数的影响(因为relu偏向正的),而当\(f\)是恒等映射的时候信号可以直接在两个单元之间传递,所以训练loss下降的就非常块了;而相对于更少的层如164层,这个现象就不太明显了;
- 减少过拟合。这时候虽然在训练集合上有稍微更高的loss,可是在测试集上有更低的错误,我们认为在原始结构中,虽然BN负责归一化信息,可是却很快的与快捷连接的输出相加,信号又变得不归一化了。而这样的设计就保证了BN归一化的信息是直接送入ReLU的




