Feature Extractor[batch normalization]
1 - 背景
摘要:因为随着前面层的参数的改变会导致后面层得到的输入数据的分布也会不断地改变,从而训练dnn变得麻烦。那么通过降低学习率和小心地参数初始化又会减慢训练过程,而且会使得具有饱和非线性模型的训练变得很困难。我们将这种现象叫做internal covariate
shift。BN通过对输入进行归一化从而解决这个问题。在这其中,作者试图让归一化成为模型结构的一部分,并且对每个训练的mini-batch都进行归一化。最后的结果是bn方法可以让我们使用更大的学习率和不用那么小心的初始化。而且BN同样也扮演着正则化的角色,例如可以代替dropout的使用。将BN用在一些图像分类模型上的话,可以在达到同等准确度的基础上将模型训练的时间减少14倍之多。而且最后的模型表现要优于没用bn的。
我们知道目前的深度学习训练都是基于mini-batch的,如果batch size越接近1,那么就越是随机梯度下降,如果越接近整个数据集,那么就越是批量下降。所以针对mini-batch的处理,是一个折中的方法,不过因为mini-batch一定程度上是可以代表整个训练集的,而且也容易并行化。虽然随机梯度下降很有效,但需要很小心的初始化模型的参数,每一层的输入都受到了前面几层的影响,所以前面每层一点点小小的变化都会在后面的层里累计放大。这也是预训练中的道理,如《Why Does Unsupervised Pre-training Help Deep Learning》等就也说到,越是前期的影响,那么本身所占的影响就越大,因为会不断的累积下去。
这里我们要着重说下covariate shift,因为BN的出现主要就是为了解决深度学习这个很久就提出的问题了。即当一个训练好的系统的输入分布改变的时候,我们称之为covariate shift(其实就是训练样本的分布和测试样本分布不一致)。这通常通过领域自适应来解决(如迁移学习)。然而作者认为covariate shift的概念可以从整个系统扩展到系统的具体部分上,如子网络或者某一层。从而也叫做internal covariate shift。当然从下面的参考文献1中,更细化的知道了,前者是一个迁移学习领域的问题,而后者是作者借鉴了该概念,实而是一个优化问题。
我们都知道目前的神经网络都是一层一层的,而高层可以看成是低层的一个函数映射,如:
假如:
那么:
因此,如果随着时间的推移\(x\)的分布一直保持固定是有利的;\(\Theta_2\)就不需要再去重新调整分布从而去适应\(x\)的分布变化。即每次前面层的参数改变,就会导致输出的值的分布也会改变,从而后面的层就需要调整去适应前面层输出值的分布变化。
假设我们有一层网络,其中的激活函数是sigmoid。如\(g(x)=\frac{1}{1+exp(-x)}\)。那么随着\(|x|\)的变大,\(g^{'}(x)\)会趋近于0。这也就意味着,在\(x\)的所有维度上,除了那些绝对值较小的值,其他维度上的梯度都会趋近于消失,从而导致模型训练的很慢。然而\(x\)也受到当前层下面那些层的参数的影响。在训练中改变那些参数,会很大程度上将\(x\)的许多维度上的值逼近于非线性的饱和区域,从而减慢了收敛的过程。虽然饱和问题和逐渐消失的梯度可以通过使用relu和小心地初始化去解决。然而如果我们确保非线性输入的分布随着网络的训练还是会很稳定,那么优化器会更少的陷入饱和的境地,从而就能够加速训练了。
换句话说,我们将在训练过程中,深度网络的内部节点的分布的变化叫做Internal Covariate shift。如果能消除这种现象,就能加速训练了。所谓的BN方法就是通过归一化来修复层输入的均值和方差;同样bn可以减少梯度对参数的量纲和初始化的依赖。
2 - BN
早在98年,Lecun等人就发现,如果对输入数据进行白化预处理(对输入数据进行线性变换,使得数据具有0均值,单位方差,并进行解相关),那么就能加速网络的收敛。那么可推出:当每层观察由下面层的输出作为输入时,如果能够对该输入进行相同的白化,那么是有益的。从而实现固定的输入分布,消除internal covariate shift的不良影响。
我们本可以考虑在每个训练步骤或者某些中间部分对激活值进行白化操作。比如直接修改网络或者修改最优化算法中的参数,这都取决于网络的激活值。然而,如果这些修改与优化步骤相互穿插,那么梯度下降部分就会以需要更新归一化的方式去更新这些参数,这样就减少了梯度步长的影响了。
ps:文章第二部分主要介绍了归一化需要放入整个梯度下降部分中去考虑,不能独立于梯度下降而存在,否则会造成如偏置一直再增大,即使loss不下降了,还是会无限增大。
因为对每一层的输入都进行完整的白化是非常耗时的(需要所有训练数据过一遍之前的层,从而得到当前层输入,计算协方差矩阵,进行白化,得到当前层的输出,然后基于输入的协方差再计算白化;然后所有数据过下一层,如前面一层一样的白化操作;而且一次BP之后,之前得到的协方差矩阵又得重新计算),而且不是每个地方都是可微的,所以需要进行改进,:
- 1 - 通过对每个特征维度单独进行归一化,让每个特征维度具有0均值和1方差,而不是同时对层的输入和输出做白化;
假设一层的输入为\(x=(x^{(1)},...,x^{(d)})\),那么我们对每个维度归一化:
这本是基于整个训练集计算的,通过98年Lecun等人的工作我们可以看到,这样可以加速收敛,而且即使特征没有解相关也可以加速。
可是这样简单的对一层的每个输入进行归一化会破坏该层的表征。例如归一化一个sigmoid的输入会限制它只能表示其函数的线性部分。为了解决这个问题,我们需要确保插入网络的变换可以依然表示之前的同一个分布。所以作者对每个激活值\(x^{(k)}\)引入了新的2个变量\(\gamma^{(k)},\beta^{(k)}\),从而对归一化后的值进行缩放和平移:
这些参数都是随着原来的模型参数一起训练得到的,从而修复网络的表征能力。确实,如果设定\(\gamma^{(k)}=\sqrt{Var[x^{(k)}]}\)和\(\beta^{(k)}=E[x^{(k)}]\),最理想情况下,我们可以修复之前的激活值。
- 2 - 在批处理操作下,我们的每次训练步骤都是基于整个数据集的,所以我们可以直接对整个训练集进行归一化,而在mini-batch下就没办法了。所以需要做第二个改进:每个mini-batch都生成对每个激活值的均值和方差的估算。这样的话,归一化就能完全参与整个梯度BP了。

图2.1 BN的过程
如图2.1 就是整个BN的过程了,我们可以从另一个角度来解释这个过程:
假设网络层的输入为\(x\),而我们基于输入,成功的计算得到了其归一化后的结果:\(\hat x\),然后我们再设计一层线性变换层,即增加一层子网络,该层的作用就是\(y^{(k)}=\gamma^{(k)}\hat x^{(k)}+\beta^{(k)}\)。然后将这一层的输出,才真的作为下一层的输入。换句话说就是在原来的每一层网络之间增加了一层线性的数值归一化层,只是这一层不可见罢了。
而这些子网络的输入都是具有固定0均值和1方差的,通过增加这一层BN层,使得学到的仿射变换能够去修复之前的数据分布和保留网络的表达能力,而其中的\(\gamma,\beta\)都是基于网络自己决定的(当然也是网络基于数据决定的)
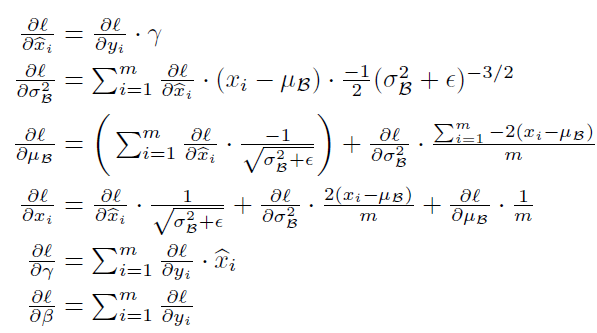
图2.2 BN的BP推导

图2.3 基于BN的训练和预测的过程
在训练阶段的期望和方差是基于每个mini-batch计算的;在inference阶段,为了保证一致性,是先对整个训练集计算期望和方差的,而为了防止单独的再去过一遍训练集,是基于每个mini-batch计算整体的期望和无偏估计方差的
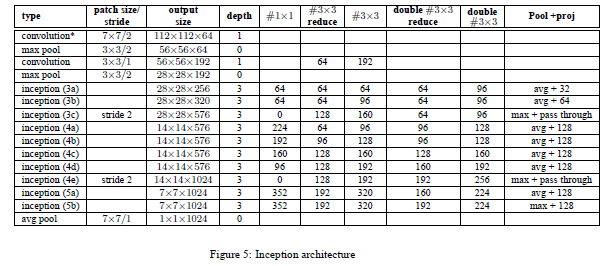
图2.4 inception v2 结构图
参考文献:
[1] - 从Bayesian角度浅析Batch Normalization




