opencv6.3-imgproc图像处理模块之边缘检测

接opencv6.2-improc图像处理模块之图像尺寸上的操作

本文大部分都是来自于转http://www.opencv.org.cn/opencvdoc/2.3.2/html/doc/tutorials/imgproc/table_of_content_imgproc/table_of_content_imgproc.html#table-of-content-imgproc ，只是个按照自己想法的组织罢了。

六、边缘检测

其实边缘检测就是首先将图像的值作为一个函数的结果值，然后在其函数空间中，如果是那些平稳变化的，那么就差不多是相同像素值，而所谓的边缘就是两边的像素值相差较大的地方，从函数空间的角度来说，就是这个地方会有突变，也就是会有导数比较大的情况，所以在这样的方法看待图像从而得知，可以通过求导的方式来得到图像的边缘。在《数字图像处理，第二版》的463页的边缘检测部分就比较详细的说明了如何可以用函数求导的方式来计算图像的边缘。

上图左边就是假设像素值从左往右是从小到大变化的，可以看出中间就是理想的边缘位置，右边的图就是对这个用函数来表示的像素进行求导，看得出来导数在边缘的地方是最大的。我们可以推论：检测边缘可以通过定位梯度值大于邻域的相素的方法找到(或者推广到大于一个阀值)

1、sobel算子

这部分知识来自于：    http://www.opencv.org.cn/opencvdoc/2.3.2/html/doc/tutorials/imgproc/imgtrans/sobel_derivatives/sobel_derivatives.html#sobel-derivatives 直接搬过来的

Sobel 算子是一个离散微分算子 (discrete differentiation operator)。 它用来计算图像灰度函数的近似梯度。

  Sobel 算子结合了高斯平滑和微分求导。

假设被作用图像为 I:

1. 在两个方向求导:

   1. 水平变化: 将I与一个奇数大小的内核 进行卷积。比如，当内核大小为3时, 的计算结果为:

      b.垂直变化: 将:math:I与一个奇数大小的内核  进行卷积。比如，当内核大小为3时,  的计算结果为:

  2.在图像的每一点，结合以上两个结果求出近似 梯度:

有时也用下面更简单公式代替:

在《数字图像处理》中文版第二版一书的469页有说明这个算子，其中所用的卷积核也是这样的数值，在书的468页中有说明，其中的卷积核中的数值是当前局部感受野对应这个卷积核模板的感应值，中间使用系数2，是用来强调中心的重要性并且有一定的平滑效果，另一个叫做Prewitt算子。也就是说数值就是这么定的。

Notes:当内核大小为 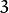 时, 以上Sobel内核可能产生比较明显的误差(毕竟，Sobel算子只是求取了导数的近似值)。 为解决这一问题，OpenCV提供了 Scharr 函数，但该函数仅作用于大小为3的内核。该函数的运算与Sobel函数一样快，但结果却更加精确，其内核为:

int scale = 1;
  int delta = 0;
  int ddepth = CV_16S;

// 创建 grad_x 和 grad_y 矩阵
  Mat grad_x, grad_y;
  Mat abs_grad_x, abs_grad_y;

//示例代码中是先图像进行高斯平滑的 然后在转换成灰度图
//src_gray 为读取的图像转换成灰度图

  /// 求 X方向梯度
  //Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, BORDER_DEFAULT );
  Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );
  convertScaleAbs( grad_x, abs_grad_x );

  /// 求Y方向梯度
  //Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, BORDER_DEFAULT );
  Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );
  convertScaleAbs( grad_y, abs_grad_y );

  /// 合并梯度(近似)
  addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );

  imshow( window_name, grad );

函数原型：void Sobel(InputArray src, OutputArray dst, int ddepth, int dx, int dy, int ksize=3, double scale=1,double delta=0, int borderType=BORDER_DEFAULT );

参数列表：输入图像、输出图像、输出图像的深度、x方向求导的阶数，y方向求导的阶数、sobel核的扩张的尺寸、为了计算导数的可选的缩放因子、在结果存储到dst前与结果相加的可选的delta值、边界类型。

输入图像：无

输出图像：与输入具有相同的尺寸和通道

输出图像的深度：

– src.depth() = CV_8U, ddepth = -1/CV_16S/CV_32F/CV_64F
– src.depth() = CV_16U/CV_16S, ddepth = -1/CV_32F/CV_64F
– src.depth() = CV_32F, ddepth = -1/CV_32F/CV_64F

– src.depth() = CV_64F, ddepth = -1/CV_64F

当ddepth等于 -1 是，目标图像有着与源图像一样的depth；当输入是8-bit的时候，它会生成截断的导数（个人：这里我暂时也不懂）

ksize:默认情况下没有缩放；必须是正的，而且是奇数

其他参数：略

在其他情况下是使用ksize×ksize的分离核用来计算导数。当ksize=1，那么就使用3×1或者1×3的核（这时候imeiyou高斯平滑了）。ksize=1只被用来第一次或者第二次的x方向-或者y方向-的导数。

有个特殊的值ksize = CV_SCHARR(-1)是使用3×3的Scharr过滤器，比3×3的sobel更具准确性:

这是x方向的求导，转置就可以成为y方向的求导

sobel函数是通过对图像使用一个合适的核来卷积来进行求导的：

sobel算子是结合了高斯平滑和微分的，所以结果或多或少对噪音具有不变性。最多的这个函数会使用（xorder = 1，yorder = 0，ksize=3）或者（xorder = 0，yorder = 1，ksize = 3）来计算第一次的x方向或者y方向的导数。

2、laplace算子

上面的sobel算子是在边缘部分求一次导数，如果说求第二次导数呢？：

你会发现在一阶导数的极值位置，二阶导数为0。所以我们也可以用这个特点来作为检测图像边缘的方法。 但是， 二阶导数的0值不仅仅出现在边缘(它们也可能出现在无意义的位置),但是我们可以过滤掉这些点。

从以上分析中，我们推论二阶导数可以用来 检测边缘 。 因为图像是 “2维”, 我们需要在两个方向求导。使用Laplacian算子将会使求导过程变得简单。

Laplacian 算子 的定义:

OpenCV函数 Laplacian 实现了Laplacian算子。 实际上，由于 Laplacian使用了图像梯度，它内部调用了 Sobel 算子。

Mat src, src_gray, dst;
  int kernel_size = 3;
  int scale = 1;
  int delta = 0;
  int ddepth = CV_16S;//因为输入图像的深度是 CV_8U ，这里我们必须定义 ddepth = CV_16S 以避免外溢。

GaussianBlur( src, src, Size(3,3), 0, 0, BORDER_DEFAULT );
  /// 转换为灰度图
  cvtColor( src, src_gray, CV_RGB2GRAY );
  /// 使用Laplace函数
  Mat abs_dst;
  Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, BORDER_DEFAULT );
  convertScaleAbs( dst, abs_dst );
  /// 显示结果
  imshow( window_name, abs_dst );

上面是例子代码

函数原型：void Laplacian(InputArray src, OutputArray dst, int ddepth, int ksize=1, double scale=1, double delta=0, int borderType=BORDER_DEFAULT );

参数列表：原图像、目标图像、目标图像的深度、计算二阶导数过滤器大小、计算拉普拉斯的可选的缩放因子、在存储到dst前添加的delta值、边界类型。

这个函数通过添加第二次的x和y方向上的求导来计算源图像的拉普拉斯，是通过使用sobel算子来实现的：

当ksize>1的时候是这样的，不过当ksize=1的时候，这个拉普拉斯是通过对图像使用下面的过滤器来实现的：

ps：想要知道如何使用sobel来实现这个的，就需要看他的cpp实现代码了，暂时没去找。

3、canny边缘检测

Canny 边缘检测算法 是 John F. Canny 于 1986年开发出来的一个多级边缘检测算法，也被很多人认为是边缘检测的 最优算法, 最优边缘检测的三个主要评价标准是:

低错误率: 标识出尽可能多的实际边缘，同时尽可能的减少噪声产生的误报。

高定位性: 标识出的边缘要与图像中的实际边缘尽可能接近。

最小响应: 图像中的边缘只能标识一次。

原理：

a、消除噪声。 使用高斯平滑滤波器卷积降噪。 下面显示了一个 size=5的高斯内核示例：

b、计算梯度幅值和方向。 此处，按照Sobel滤波器的步骤:

   i）运用一对卷积阵列 (分别作用于 x 和 y 方向):

   ii）使用下列公式计算梯度幅值和方向:

    梯度方向近似到四个可能角度之一(一般 0, 45, 90, 135)

c、非极大值 抑制。 这一步排除非边缘像素， 仅仅保留了一些细线条(候选边缘)。

d、滞后阈值: 最后一步，Canny 使用了滞后阈值，滞后阈值需要两个阈值(高阈值和低阈值):

   i）如果某一像素位置的幅值超过 高 阈值, 该像素被保留为边缘像素。

   ii）如果某一像素位置的幅值小于 低 阈值, 该像素被排除。

   iii）如果某一像素位置的幅值在两个阈值之间,该像素仅仅在连接到一个高于 高 阈值的像素时被保留。

   Canny 推荐的 高:低 阈值比在 2:1 到3:1之间。

e、想要了解更多细节，你可以参考任何你喜欢的计算机视觉书籍。

Mat dst, detected_edges;

int edgeThresh = 1;
int lowThreshold;
int const max_lowThreshold = 100;
int ratio = 3;
int kernel_size = 3;

/// 原图像转换为灰度图像
  cvtColor( src, src_gray, CV_BGR2GRAY );

/// 使用 3x3内核降噪
  blur( src_gray, detected_edges, Size(3,3) );
  /// 运行Canny算子
  Canny( detected_edges, detected_edges, lowThreshold, lowThreshold*ratio, kernel_size );
/// 创建与src同类型和大小的矩阵(dst)
  dst.create( src.size(), src.type() );
  /// 使用 Canny算子输出边缘作为掩码显示原图像  

dst = Scalar::all(0);  src.copyTo( dst, detected_edges);///copyTo 将 src 图像拷贝到 dst . 但是，仅仅拷贝掩码不为0的像素。既然Canny边缘检测的输出是镶嵌在黑色背景中的边缘像素，因此其结果 dst图像除了被检测的边缘像素，其余部分都为黑色  imshow( window_name, dst );

函数原型：void Canny(InputArray image, OutputArray edges, double threshold1, double threshold2, int apertureSize=3, bool L2gradient=false );

参数列表：输入图像、输出图像、低阈值、高阈值、给sobel（）算子的核大小、一个标识；

输入图像：单通道的8-bit图；（在2.4.10版本的refman中还是说单通道的，但是却能直接调用彩色图像，不过在3.0版本的refman中已                 经忽略了单通道的要求，只需要8-bit即可，所以1、经常注意refman；2、不同版本还是有差别的）。

输出边缘图：和输入图像一样的尺寸和类型

低限阈值：如果某一像素位置的幅值小于 低 阈值, 该像素被排除；

高限阈值：如果某一像素位置的幅值超过 高 阈值, 该像素被保留为边缘像素。

标识：用来指示是否使用一个更准确的L2范数 = 来计算图像梯度大小（true）；或者使用默认的L1范数=来计算图像梯度大小（false）。

介于低限阈值与高限阈值之间的最小值用来作为边缘连接；最大的值用来查找强边缘的初始化分割。（个人：最小值用来连接两个相邻的边缘，而最大值用来首先查找最强的边缘，通过固定高限阈值，用滑动条来改变低限阈值就可以发现图像的边缘是先最强的几条，然后是一点点的扩大并将相连的边缘连接起来）。

七、霍夫变换

在《数字图像处理》中文版第二版中475页有霍夫变换的介绍。这里暂时略，待以后补充

1、线检测

霍夫线变换是一种用来寻找直线的方法.

是用霍夫线变换之前, 首先要对图像进行边缘检测的处理，也即霍夫线变换的直接输入只能是边缘二值图像.

原理：

a、众所周知, 一条直线在图像二维空间可由两个变量表示. 例如:

      i）在 笛卡尔坐标系: 可由参数: （m，b）斜率和截距表示.

      ii）在 极坐标系: 可由参数: （r，theta）极径和极角表示

     对于霍夫变换, 我们将用 极坐标系 来表示直线. 因此, 直线的表达式可为:

    化简得:

b、一般来说对于点, 我们可以将通过这个点的一族直线统一定义为:

   这就意味着每一对  代表一条通过点 的直线

c、如果对于一个给定点  我们在极坐标对极径极角平面绘出所有通过它的直线, 将得到一条正弦曲线. 例如, 对于给定点        x0=8 and y0=6 我们可以绘出下图 (在平面 theta-r):

   只绘出满足下列条件的点 r >0 和 0<theta <2*pi；

d、我们可以对图像中所有的点进行上述操作. 如果两个不同点进行上述操作后得到的曲线在平面 theta-r 相交, 这就意味着它们通过    同一条直线. 例如, 接上面的例子我们继续对点:x1 = 9，y1 = 4和点x2 = 12，y2 = 13画图, 得到下图:

   这三条曲线在 （theta - r ）平面相交于点 （0.925，9.6）， 坐标表示的是参数对（theta ，r） 或者是说点（x0，y0），点      （x1，y1） 和点（x2，y2）  组成的平面内的的直线.

e、那么以上的材料要说明什么呢? 这意味着一般来说, 一条直线能够通过在平面 theta-r 寻找交于一点的曲线数量来 检测. 越多曲    线交于一点也就意味着这个交点表示的直线由更多的点组成. 一般来说我们可以通过设置直线上点的 阈值 来定义多少条曲线交于    一点我们才认为 检测 到了一条直线.

f、这就是霍夫线变换要做的. 它追踪图像中每个点对应曲线间的交点. 如果交于一点的曲线的数量超过了 阈值, 那么可以认为这个交    点所代表的参数对 在原图像中为一条直线.

OpenCV实现了以下两种霍夫线变换:

a、标准霍夫线变换：原理在上面的部分已经说明了. 它能给我们提供一组参数对 的集合来表示检测到的直线；在OpenCV 中通过函数 HoughLines 来实现

b、统计概率霍夫线变换：这是执行起来效率更高的霍夫线变换. 它输出检测到的直线的端点；在OpenCV 中它通过函数 HoughLinesP 来实现

 Mat dst, cdst;
 Canny(src, dst, 50, 200, 3);//先进行求边缘
 cvtColor(dst, cdst, CV_GRAY2BGR);//灰度图再次转换成彩色图

 //标准霍夫线变换
  vector<Vec2f> lines;
  HoughLines(dst, lines, 1, CV_PI/180, 100, 0, 0 );//标准霍夫线变换 这里rho =1，theta = 1度；

  for( size_t i = 0; i < lines.size(); i++ )
  {
     float rho = lines[i][0], theta = lines[i][1];
     Point pt1, pt2;
     double a = cos(theta), b = sin(theta);
     double x0 = a*rho, y0 = b*rho;
     pt1.x = cvRound(x0 + 1000*(-b));
     pt1.y = cvRound(y0 + 1000*(a));
     pt2.x = cvRound(x0 - 1000*(-b));
     pt2.y = cvRound(y0 - 1000*(a));
     line( cdst, pt1, pt2, Scalar(0,0,255), 3, CV_AA);//画线
  }
 //统计概率霍夫线变换
  vector<Vec4i> lines;
  HoughLinesP(dst, lines, 1, CV_PI/180, 50, 50, 10 );//统计概率霍夫线变换
  for( size_t i = 0; i < lines.size(); i++ )
  {
    Vec4i l = lines[i];
    line( cdst, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(0,0,255), 3, CV_AA);//画线
  }
 imshow("source", src);
 imshow("detected lines", cdst);

标准-函数原型：void HoughLines(InputArray image, OutputArray lines, double rho, double theta, int threshold, double srn=0, double stn=0 );

参数列表：输入图像、存储的线的容器、r半径、theta角度、阈值、距离分辨率rho的除数、距离分辨率theta的除数；

输入图像：8-bit的，而且是单通道二值图像；

第二个参数-线：vector容器对象，其中每条线由一个二元向量（）表示。r 表示从坐标原点（0，0）（图像的左上角）到这点的距离；theta 表示以弧度制为单位的角度（0 表示垂直线；pi/2 表示水平线）；

第三个参数：以像素为单位的累加器中的距离分辨率；

第四个参数：以弧度为单位的累加器中的角度分辨率；

第五个参数：累加器阈值参数。只有当累加的值>阈值 ,线条才会被返回（也就是算这是一条线）；

第六个参数：对于多尺度霍夫变换来说，这是一个关于距离分辨率rho（第三个参数rho）的除数。粗度累加器的距离分辨率是rho，精确的累加器的分辨率是rho/srn。如果srb=0而且stn=0，那么使用经典的霍夫变换；不然这两个参数都该是正数（最后两个参数）；

第七个参数：对于多尺度霍夫变换，这是距离分辨率theta的一个除数。

对于这个函数有三种不同的表示方法，不过这几个方法都是依赖参数来实现的，本身没法赋值：

– CV_HOUGH_STANDARD      经典或者说是标准霍夫变换. 每一条线都是由两个floating-point（ 浮动点）数（r，theta）来表示的，这里r表示原点（0，0）与这条线之间的距离，theta表示这条线与x轴之间的夹角。所以矩阵（生成的序列，也就是存储线的vector容器）必须是CV_32FC2类型的。

– CV_HOUGH_PROBABILISTIC  概率霍夫变换（如果图片包含着一些长的直线段，那么这个方法更有效）。它返回的是直线段，而不是整条线，没挑线段由它的起始点和末端点表示，这个矩阵（生成的序列）必须是CV_32SC4类型。
– CV_HOUGH_MULTI_SCALE     经典霍夫变换的多尺度不变性。这些直线以与CV_HOUGH_STANDAED的方式编码
param1 – First method-dependent parameter:
–  对于经典霍夫变换, 这个参数不使用，默认为0.
–  对于概率霍夫变换, 直线段长度的最小值.
– 对于多尺度霍夫变换, 这个参数就是 srn.
param2 – Second method-dependent parameter:
–  对于经典霍夫变换, 这个参数不使用，默认为0.
–  对于概率霍夫变换, 这个参数是介于位于同一条直线上不同的线段之间的最大间隔，用来合并多条属于相同的直线的线段.
– 对于多尺度霍夫变换, 这个参数就是 stn.

统计-函数原型：void HoughLinesP(InputArray image, OutputArray lines, double rho, double theta, int threshold, double minLineLength=0, double maxLineGap=0 );

参数列表：原图像、输出的线的vector容器、半径、角度、阈值、最小的线段长度、最大的线段间隔；

第一个参数：8-bit的单通道二值图像。图像有可能会被这个函数所修改；

第二个参数：输出线的vector容器，每条线由一个4元素的向量组成（x1，y1，x2，y2），这里（x1，y1）和（x2，y2）是检测到的每条线段的两个端点。

第三个参数：以像素为单位的累加器的距离分辨率；

第四个参数：以弧度为单位的累加器的角度分辨率；

第五个参数：只有超过这个阈值的结果才被作为检测到的线段；

第六个参数：当检测到的线段小于这个值就抛弃，不返回；

第七个参数；在归属同一条直线上允许不同线段之间的最大间隔，小于这个间隔就将这分离的线段连起来。

2、圆检测

    霍夫圆变换的基本原理和霍夫线变换类似, 只是点对应的二维极径极角空间被三维的圆心点x, y还有半径r空间取代.

    对直线来说, 一条直线能由参数极径极角 (r，theta) 表示. 而对圆来说, 我们需要三个参数来表示一个圆, 如上文所说现在原图像的边缘图像的任意点对应的经过这个点的所有可能圆是在三维空间有下面这三个参数来表示了，其对应一条三维空间的曲线. 那么与二维的霍夫线变换同样的道理, 对于多个边缘点越多这些点对应的三维空间曲线交于一点那么他们经过的共同圆上的点就越多，类似的我们也就可以用同样的阈值的方法来判断一个圆是否被检测到, 这就是标准霍夫圆变换的原理, 但也正是在三维空间的计算量大大增加的原因, 标准霍夫圆变化很难被应用到实际中:

这里的 （Xcenter,Ycenter）表示圆心的位置 (下图中的绿点) 而 r 表示半径, 这样我们就能唯一的定义一个圆了, 见下图:

    出于上面提到的对运算效率的考虑, OpenCV实现的是一个比标准霍夫圆变换更为灵活的检测方法: 霍夫梯度法, 也叫2-1霍夫变换(21HT), 它的原理依据是圆心一定是在圆上的每个点的模向量上, 这些圆上点模向量的交点就是圆心, 霍夫梯度法的第一步就是找到这些圆心, 这样三维的累加平面就又转化为二维累加平面. 第二部根据所有候选中心的边缘非0像素对其的支持程度来确定半径. 21HT方法最早在Illingworth的论文The Adaptive Hough Transform中提出并详细描述, 也可参照Yuen在1990年发表的A Comparative Study of Hough Transform Methods for Circle Finding。 Bradski的《学习OpenCV》一书则对OpenCV中具体对算法的具体实现有详细描述并讨论了霍夫梯度法的局限性.

/// 转换成灰度
  cvtColor( src, src_gray, CV_BGR2GRAY );

  /// 减少噪音来避免错误的圆检测
  GaussianBlur( src_gray, src_gray, Size(9, 9), 2, 2 );

  vector<Vec3f> circles;

  /// 使用霍夫变换去寻找圆
  HoughCircles( src_gray, circles, CV_HOUGH_GRADIENT, 1, src_gray.rows/8, 200, 100, 0, 0 );

  /// 将检测到的圆画出来
  for( size_t i = 0; i < circles.size(); i++ )
  {
      Point center(cvRound(circles[i][0]), cvRound(circles[i][1]));
      int radius = cvRound(circles[i][2]);
      // circle center
      circle( src, center, 3, Scalar(0,255,0), -1, 8, 0 );
      // circle outline
      circle( src, center, radius, Scalar(0,0,255), 3, 8, 0 );
   }

  /// 显示结果
  namedWindow( "Hough Circle Transform Demo", CV_WINDOW_AUTOSIZE );
  imshow( "Hough Circle Transform Demo", src );

上面是例子代码。

函数原型：void HoughCircles(InputArray image, OutputArray circles, int method, double dp, double minDist,double param1 = 100, double param2=100, int minRadius=0, int maxRadius=0 );

参数列表：输入图像、输出的圆的vector容器、检测用的方法、累加器图像的反比分辨率、检测到圆心之间的最小距离、Canny边缘函数的高阈值、圆心检测阈值、能检测到的最小圆半径、能检测到的最大圆半径；

第一个参数：8-bit的单通道灰度图；

第二个参数：包含找到圆的vector，每个向量由3元素的floating-point（浮动点，即不固定点）向量组成（x，y，radius）；

第三个参数：使用的方法，当前可以使用的方法只有CV_HOUGH_GRADENT;

第四个参数：累加器分辨率到图像分辨率的反比例。例如：如果dp=1，累加器有着和输入图像一样的分辨率；如果dp=2，累加器有着输入图像的width和height一半的值；

第五个参数：介于检测到的圆的中心的最小距离。如果这个参数太小，在真的圆形周围会检测到很多假的圆。如果太大，一些圆会被miss掉

第六个参数：第一个方法依赖的参数。当使用CV_HOUGH_GRADIENT,这个参数表示传递给canny检测器的高限阈值，（低限阈值是这个值的一半）

第七个参数：第二个方法依赖的参数。在CV_HOUGH_GRADIENT中。这个参数是在检测阶段中原型的累加器阈值，这个值越小，越多假的圆会被检测到，对应于越大的累加值，越先返回（个人：也就是进行排序，累加值越大，说明圆的可能性越高）

后两个参数：略

八、坐标映射和仿射变换

1、remapping重映射

把一个图像中一个位置的像素放置到另一个图片指定位置的过程.

  为了完成映射过程, 有必要获得一些插值为非整数像素坐标,因为源图像与目标图像的像素坐标不是一一对应的.

我们通过重映射来表达每个像素的位置 （x，y）:

   这里 g（）是目标图像,f（） 是源图像,h(x,y) 是作用于(x,y) 的映射方法函数.

让我们来思考一个快速的例子. 想象一下我们有一个图像 I , 我们想满足下面的条件作重映射:

会发生什么? 图像会按照 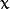 轴方向发生翻转. 例如, 源图像如下:

  

看到红色圈关于 x的位置改变( x 轴水平翻转):就是相当于照镜子一样。

 /// Create dst, map_x and map_y with the same size as src:
  dst.create( src.size(), src.type() );
  map_x.create( src.size(), CV_32FC1 );
  map_y.create( src.size(), CV_32FC1 );

 /// 下面是四种更新mapx和mapy的方法

 ind = ind%4;

   for( int j = 0; j < src.rows; j++ )
   { for( int i = 0; i < src.cols; i++ )
       {
         switch( ind )
         {
           case 0:
             if( i > src.cols*0.25 && i < src.cols*0.75 && j > src.rows*0.25 && j < src.rows*0.75 )
               {
                 map_x.at<float>(j,i) = 2*( i - src.cols*0.25 ) + 0.5 ;
                 map_y.at<float>(j,i) = 2*( j - src.rows*0.25 ) + 0.5 ;
                }
             else
               { map_x.at<float>(j,i) = 0 ;
                 map_y.at<float>(j,i) = 0 ;
               }
                 break;
           case 1:
                 map_x.at<float>(j,i) = i ;
                 map_y.at<float>(j,i) = src.rows - j ;
                 break;
           case 2:
                 map_x.at<float>(j,i) = src.cols - i ;
                 map_y.at<float>(j,i) = j ;
                 break;
           case 3:
                 map_x.at<float>(j,i) = src.cols - i ;
                 map_y.at<float>(j,i) = src.rows - j ;
                 break;
         } // end of switch
       }
    }
  ind++;

  remap( src, dst, map_x, map_y, CV_INTER_LINEAR, BORDER_CONSTANT, Scalar(0,0, 0) );

函数原型：void remap(InputArray src, OutputArray dst, InputArray map1, InputArray map2, int interpolation,int borderMode = BORDER_CONSTANT, const Scalar& borderValue=Scalar());

参数列表：输入图像、输出图像、x方向的映射参数、y方向的映射参数、插值方法、像素插值方法、边界常数值；

第一个参数：略

第二个参数：有着与原图像一样的类型和map1一样的尺寸；

第三个参数：第一个映射图，不论是点（x，y）还是只有x的值是类型CV_16SC2、CV_32FC1、CV_32FC2。（可见convertMaps()，详细的           关于将floating点转换成固定点来加速）。它相当于方法 h（x，y）的第一个参数。

第四个参数：第二个映射，这里y值为CV_16UC1、CV_32FC1或者为空（当map1是（x，y）点而不是单独的x的时候）。

第五个参数：在resize（）函数中有具体的插值方法介绍，不过这里方法INTER_AREA没有被支持。

    – INTER_NEAREST - 最近邻插值
    – INTER_LINEAR - 双线性插值 (used by default)
    – INTER_AREA -   使用像素区域相关的重采样。 它作为图像抽取的一个优先选择的方法，因为它可以得到moire’-free的结果.    不过当图像变焦（zoom，也是缩放的意思）的时候，这相似于INTER_NEAREST方法。
    – INTER_CUBIC -  基于4×4的像素周边的双三次插值
    – INTER_LANCZOS4 - 基于8×8的像素周边的Lanczos插值

第六个参数：像素插值方法。当borderMode = BORDER_TRANSPARENT，这说明在目标图像中的像素是对应于输入图像中                           的“outliers”，不会被这个函数修改.

第七个参数：当使用常量边界的时候使用，默认为0。

这个函数是通过下面的方法来转换的：

 

那些非整数坐标的像素的值通过使用一个可用的插值的方法计算得到。mapx和mapy可以分别在map1和map2中使用floating-point（浮动点）映射进行编码，或者在map1中的（x，y）的交叉浮动点映射，或者使用convertMaps（）来进行固定点映射得到。你想要将一个映射的表征从浮动点转换到固定点的原因大致是因为他们可以有着（～2x）倍的加速映射操作。在转换的时候，map1包含对（cvFloor（x），cvFloor(y)）和map2包含内插系数表的索引。

该函数可以支持in-place，注意 map_y 和 map_x 与 src 的大小一致。

2、仿射变换

一个任意的仿射变换都能表示为 乘以一个矩阵 (线性变换) 接着再 加上一个向量 (平移).

  我们能够用仿射变换来表示:旋转 (线性变换)；平移 (向量加)；缩放操作 (线性变换)。

 事实上, 仿射变换代表的是两幅图之间的 关系 ， 我们通常使用 2x3的矩阵来表示仿射变换.

考虑到我们要使用矩阵 A和B 对二维向量 做变换,所以也能表示为下列形式:

   或者 

   仿射变换基本表示的就是两幅图片之间的 联系 . 关于这种联系的信息大致可从以下两种场景获得:

a、我们已知 X和T 而且我们知道他们是有联系的. 接下来我们的工作就是求出矩阵 M

b、我们已知 M 和 X. 要想求得 T. 我们只要应用算式 T= M*X 即可. 对于这种联系的信息可以用矩阵 M 清晰的表达 (即给出明确的2×3矩阵) 或者也可以用两幅图片点之间几何关系来表达.

   让我们形象地说明一下. 因为矩阵M 联系着两幅图片, 我们以其表示两图中各三点直接的联系为例. 见下图:

    点1, 2 和 3 (在图一中形成一个三角形) 与图二中三个点一一映射, 仍然形成三角形, 但形状已经大大改变. 如果我们能通过这样两组三点求出仿射变换 (你能选择自己喜欢的点), 接下来我们就能把仿射变换应用到图像中所有的点.

//定义一些需要用到的变量, 比如需要用来储存中间和目标图像的Mat和两个需要用来定义仿射变换的二维点数组

Point2f srcTri[3];//源图像的三个点
Point2f dstTri[3];//目标图像的三个点

Mat rot_mat( 2, 3, CV_32FC1 );//仿射旋转变换矩阵
Mat warp_mat( 2, 3, CV_32FC1 );//仿射变换矩阵
Mat src, warp_dst, warp_rotate_dst;//源图像、仿射变换的目标图像、仿射旋转的目标图

src = imread( argv[1], 1 );//加载源图像

warp_dst = Mat::zeros( src.rows, src.cols, src.type() );//以与源图像同样的类型和大小来对目标图像初始化

//仿射变换: 正如上文所说, 我们需要源图像和目标图像上分别一一映射的三个点来定义仿射变换:

srcTri[0] = Point2f( 0,0 );
srcTri[1] = Point2f( src.cols - 1, 0 );
srcTri[2] = Point2f( 0, src.rows - 1 );

dstTri[0] = Point2f( src.cols*0.0, src.rows*0.33 );
dstTri[1] = Point2f( src.cols*0.85, src.rows*0.25 );
dstTri[2] = Point2f( src.cols*0.15, src.rows*0.7 );

warp_mat = getAffineTransform( srcTri, dstTri );//通过这两组点, 我们能够使用OpenCV函数 getAffineTransform 来求出仿射变换，我们获得了用以描述仿射变换的 2×3矩阵 (在这里是 warp_mat)

warpAffine( src, warp_dst, warp_mat, warp_dst.size() );//将刚刚求得的仿射变换应用到源图像，这样我们就获得了变换后的图像! 我们将会把它显示出来

namedWindow( warp_window, CV_WINDOW_AUTOSIZE );
imshow( warp_window, warp_dst );//显示仿射变换的结果

仿射变换就是a、首先通过计算得到仿射变换矩阵；b、然后将这个仿射变换矩阵应用于所需要操作的图像得到目标图像。

仿射旋转：

想要旋转一幅图像, 你需要两个参数（第三个参数可选择）:a、旋转图像所要围绕的中心b、旋转的角度. 在OpenCV中正角度是逆时针的；c、可选择: 缩放因子。

Point center = Point( warp_dst.cols/2, warp_dst.rows/2 );
double angle = -50.0;//顺时针旋转50度
double scale = 0.6;//缩放因子

rot_mat = getRotationMatrix2D( center, angle, scale );//利用OpenCV函数 getRotationMatrix2D 来获得旋转矩阵, 这个函数返回一个2×3 矩阵 (这里是 rot_mat)

warpAffine( warp_dst, warp_rotate_dst, rot_mat, warp_dst.size() );//把旋转应用到仿射变换的输出

namedWindow( warp_rotate_window, CV_WINDOW_AUTOSIZE );
imshow( warp_rotate_window, warp_rotate_dst );//显示仿射旋转的结果

仿射变换函数原型：void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar());

参数列表：原图像、目标图像、转换矩阵、输出图像的尺寸、标识、边界模型、边界值；

第一个参数：略

第二个参数：输出图像有着与原图像一样的类型和dsize一样的尺寸；

第三个参数：输出图像的尺寸

第四个参数：插值方法与可选标识WARP_INVERSE_MAP的结合，WARP_INVERSE_MAP的意思就是：M是逆转换（dst->src）；

第五个参数：像素插值方法；当borderMode=BORDER_TRANSPARENT，意思就是在目标图像中的像素就是对应于原图像中的“outliers”，而且不会被该函数改变。

第六个参数：当使用常量边界的时候使用的值，默认为0；

当WARP_INVERSE_MAP标识使用的时候，这个函数将原图像转换成目标图像使用的矩阵操作是：

不然，这个变换首先是用invertAffineTransform()来反转，然后代替上面公式中的M。

该函数不支持in-place；

从点计算仿射变换矩阵的函数原型：Mat getAffineTransform(InputArray src, InputArray dst);

第一个参数：原图像中三角形顶点的坐标矩阵；

第二个参数：目标图像中三角形顶点的坐标矩阵；

该函数计算一个仿射变换的2×3矩阵：

这里：

从2d旋转中计算仿射变换的矩阵的函数原型：Mat getRotationMatrix2D(Point2f center, double angle, double scale);

第一个参数：原图像中旋转点的中心

第二个参数：以度为单位的旋转角度，正数表示逆时针（坐标的原点在图像的左上角）

第三个参数：Isotropic 缩放因子；

该函数计算矩阵：

这里：

变换可以将旋转中心映射到自身，如果不是目标值，那么就平移调整。