一、for语句的格式
for语句用来描述已知重复次数的结构。
for语句有二种格式:
1、for 控制变量:=初值 to 终值 do 语句;
2、for 控制变量:=初值 downto 终值 do 语句;
格式1称为“递增型”计数循环语句,其初值要小于或等于终值,循环才可以进行;格式2称为“递减型”计数循环语句,其初值要大于或等于终值,循环才能进行。
注意事项:
1、for语句的控制变量、初值、终值的数据类型应一致,且限于整型、布尔型和字符型等对ord函数有意义的数据类型,即序数类型
2、初值与终值一经确定,重复次数就确定不变了
3、控制变量在重复语句内不能施加任何赋值操作
4、for语句正常结束后,控制变量值无意义
例1:打印输出大写英文字符A到Z,以及对应的ASCII序号。
var
i:char;
begin
for i:='A' to 'Z' do write(i:4,ord(i):4);
end.
例2:输入N(N<=12),输出N!的值。
var
n,i,ans:longint;
begin
readln(n);
ans:=1;
for i:=1 to n do ans:=ans*i;
writeln(n,'!=',ans);
end.
例3:计算公式h(n)=1+1/2+1/3+……+1/n前n项的和。
var
i,n:integer;
h:real;
begin
readln(n);
h:=0;
for i:=1 to n do h:=h+1/i;
writeln('h=',h);
end.
例4:有一个四位的正整数,它的前两位数和后两位数之和的平方等于其本身,输出满足条件的所有正整数。
var
i,m,n:integer;
begin
for i:=1000 to 9999 do begin
m:=i div 100;
n:=i mod 100;
if sqr(m+n)=i then writeln(i);
end;
end.
思考:还有更快的算法吗?
二、循环的中止
continue:直接进入下一次循环
break:结束循环
exit:退出程序
例5:有一张纸,其厚度为0.1毫米,将它对折多少次,其厚度将超过珠穆朗玛峰的高度。
var
i:byte;
r:real;
begin
r:=0.0001;
for i:=1 to 100 do begin
r:=r*2;
if r>8848 then break;
end;
writeln(i);
end.
思考:换另外二句语句程序应该怎么改?
三、循环的嵌套
例6:打印输出九九乘法表,格式如下图
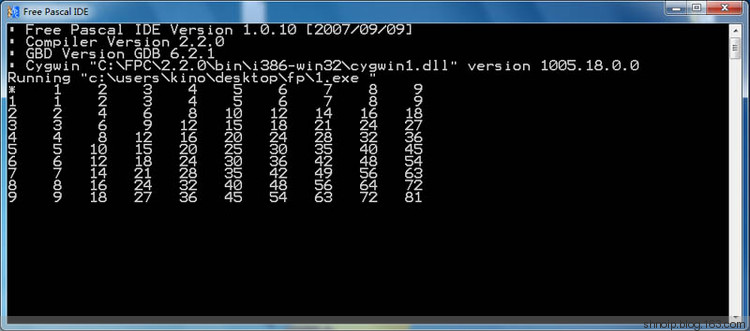
var
i,j:byte;
begin
write('*');
for i:=1 to 9 do write(i:5);
writeln;
for i:=1 to 9 do begin
write(i);
for j:=1 to 9 do write(i*j:5);
writeln;
end;
end.
例7:百钱买百鸡:用一百钱买一百只鸡,公鸡五钱一只,母鸡三钱一只,小鸡一钱买三只,每种鸡至少买一只,编程打印输出有多少种不同的买法。
var
i,j,k:byte;
begin
for i:=1 to 100 do
for j:=1 to 100 do
for k:=1 to 100 do
if (i*5+j*3+k/3=100) and (i+j+k=100)then writeln(i:10,j:10,k:10);
end.
例8:设有一个N*M方格的棋盘(1<=N,M<=100),输入N和M和值,输出该棋盘中包含有多少个正方形、多少个长方形(长方形不包括正方形)。
var
i,j,m,n:byte;
zf,cf:longint;
begin
readln(n,m);
zf:=0;cf:=0;
for i:=1 to n do
for j:=1 to m do
if i=j then zf:=zf+(m+1-j)*(n+1-i)
else cf:=cf+(m+1-j)*(n+1-i);
writeln('ZFX=',zf);
writeln('CFX=',cf);
end.
四、作业
1、zerojudge:
基础题:a059、a244、a621、b146、b202、b209、d010、d069、d072、d074、d490、d491、d498、d532、d587
for循环的嵌套:a111、b205、c005、d236
思考题:a040、a042、a148、a240、b097、c004、d881
2、求100+97+……+10+7+4+1之和。
3、在8*8的国际象棋棋盘上,第一格放一粒米,第二格放两粒米,第三格放四粒米,第四格放八粒米,以此类推,后一格是前一格的两倍,输出一共需要多少粒米。
4、鸡兔同笼49只,100条腿地上走,输出鸡和兔的数量。
5、输出所有水仙花数。所谓水仙花数是指一个三位数,如:abc,如果满足a*a*a+b*b*b+c*c*c=abc,则abc称为水仙花数。例:153=1*1*1+5*5*5+3*3*3,所以153就是水仙花数。
6、某人想将一张面值为100元的人民币兑换成5元、1元和0.5元面值的纸币,但要求零钱总数为100张,且每种面值的纸币至少有一张,输出所有兑换方法。


