由于春节，以及项目要上线的原因，导致这期的算法博文跟进的有点慢，内疚！
今天要介绍的是排序算法中的基数排序（Radix Sort），这类排序也是一个分而治之的排序，是对桶排序的一个升级和改造，也是稳定的排序。
先来说下，什么是基数排序，这里重点要理解的是【基数】这个概念，什么是基数？
说到这个，举个简单而形象的例子，比如，我们说的十进制数，是按照10为基数的典范，这里的10就是基数。分为个位，十位，百位，千位......
另外，我们常常在娱乐中用到的扑克牌，也是可以进行排序的，它有两个维度，一个是数字点数，从A到K一共13个点，这个13就是基数；另外，还可以按花色排序，分为4种：红桃，梅花，黑桃，方片。
概括而言，基数的选择和带排序的数据rd[n]的元素有关。这其中的元素rd[i]都由d个因子组成：
，而这当中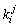
(0≤j<d)只不过是元素中的一个因子(如字符串、十进制整数等)。基数排序，则分为多因子基数排序和单因子基数排序。多因子排序中的每个因子的取值范围往往不同，比如扑克牌是两因子排序（花色，点数），而十进制整数排序，则是单因子基数排序。
设单因子的每个分量的取值范围均是：
C0≤kj≤Crd-1(0≤j<d)
可能的取值个数 rd 称为基数。
举例子概述下，方便理解：
(1) 若关键字是十进制整数，则按个、十等位进行分解，基数 rd=10，C0=0，C9=9，d 为最长整数的位数；
(2) 若关键字是小写的英文字符串，则 rd=26，Co='a'，C25='z'，d 为字符串的最大长度。
基数排序的基本思想：
将待排序的n个元素K(其中，元素的位序用j=d-1，d-2，…，0表示)，每个元素按照从低位到高位的顺序（LSD模式），分别对每个元素基于Kj（即元素的第j位大小）进行分组放入到对应的桶中。经过d轮桶排序后，n个元素就是有序的了。
基数排序的实现步骤：
1. 对待排序的n个元素进行特征分析，确定是单因子基数排序还是多因子基数排序。
2. 基于元素特征，找到基数rd。
3. 找到待排序元素中位数最多的因子，其长度d，决定要经过几轮桶排序，原始数据才有序。
4. 从最低位开始向高位（LSD）推进，对n个元素中的每一个，基于第j个因子，放入rd个桶中对应序号的一个。
5. 对rd个桶进行一次桶排序。
6. 重复4,5步骤，直到d轮桶排序结束。
上述的实现步骤，描述的已经很清楚。为了进一步将基数排序的思想描述清楚，下面，将结合一个具体的例子及代码实现，让读者更清楚的了解基数排序的真谛。
例子：
请用基数排序的思想，将下面的整数数列进行排序。
103,202,90,78,13,31,46,57,70,3,24
具体的java实现代码如下：
/** * @author "shihuc" * @date 2017年2月22日 */ package radixSort; import java.io.File; import java.io.FileNotFoundException; import java.util.ArrayList; import java.util.HashMap; import java.util.Scanner; /** * * 定义辅助类，用来记录待排序的元素的值以及该值所占据的位数。 * */ class Elem { int data; int length; /** * @return the data */ public int getData() { return data; } /** * @return the length */ public int getLength() { return length; } /** * @param data the data to set */ public void setData(int data) { this.data = data; } /** * @param length the length to set */ public void setLength(int length) { this.length = length; } } public class RadixSort { /** * @param args */ public static void main(String[] args) { File file = new File("./src/radixSort/sample.txt"); Scanner sc = null; try { sc = new Scanner(file); //获取测试例的个数 int T = sc.nextInt(); for(int i=0; i<T; i++){ int MAX = 0; //获取每个测试例的元素个数 int N = sc.nextInt(); /* * （2）获取基数rd。这里基数rd是预先指定的 */ int rd = sc.nextInt(); Elem A[] = new Elem[N]; for(int j=0; j<N; j++){ int e = sc.nextInt(); int len = getElementLength(e, rd); A[j] = new Elem(); A[j].setData(e); A[j].setLength(len); /* * （3）下面获取MAX的过程，对应基数排序实现步骤中的第3步,即获取待排序数据的最大宽度（位数） */ if(MAX < len){ MAX = len; } } radixSort(A, rd, MAX); printResult(i, A); } } catch (FileNotFoundException e) { e.printStackTrace(); } finally { if(sc != null){ sc.close(); } } } /** * 获取元素的长度 * * @param ele 待排序的某一个元素 * @param rd 基数值 * @return ele的宽度（位数） */ private static int getElementLength(int ele, int rd) { int len = 1; while(ele / rd > 0){ len++; ele = ele / rd; } return len; } /** * 获取待排序元素的第currPos+1位的值 （从低位到高位序） * * @param ele 待排序的元素 * @param rd 基数 * @param length ele的宽度（位数） * @param curPos 当前处理的是第几位 * @return 下一位对应的子元素 */ private static int getSubElem(int ele, int rd, int length, int curPos) { int subm = 0; while(ele / rd > 0 && subm <= curPos) { subm++; ele = ele / rd; } if(ele == 0 && subm <= curPos) { return -1; }else { if(ele == 0) { return 0; }else if(ele > 0 && subm > curPos) { return ele % rd; } } return -1; } /** * 基数排序的实现过程。 * * @param src 待排序的数组 * @param rd 基数 * @param max 待排序数组元素的最大宽度（位数） */ private static void radixSort(Elem src[], int rd, int max){ /* * 对待排序元素进行max轮桶排序。 for循环实现这个逻辑。 对应基数排序实现步骤中的第（6）步 */ for(int i=0; i<max; i++){ //定义rd个桶的map结构, 其中map的key表示rd的可能取值，value部分的ArrayList用来存放对应于基数范围内的某个值对应的待排序的元素 HashMap<Integer, ArrayList<Elem>> buckets = new HashMap<Integer, ArrayList<Elem>>(); /* * （4）下面的for循环，对应基数排序步骤中的第（4）步 */ for(int j=0; j<src.length; j++){ int subm = getSubElem(src[j].getData(), rd, src[j].getLength(), i-1); //当当前待处理的基数元素的值Cj不存在，即待处理的待排序元素src[j]的值data位数不够，用0代替，放入0号桶。 if(subm < 0){ subm = 0; } ArrayList<Elem> bucket = buckets.get(subm); if(bucket == null) { bucket = new ArrayList<Elem>(); buckets.put(subm, bucket); } bucket.add(src[j]); } int stPos = 0; /* * 对桶内的数据采取快速排序,并将排序后的结果映射到原始数组中作为输出。对应基数排序实现步骤中的第（5）步 */ for(int bId = 0; bId < rd; bId++){ ArrayList<Elem> bk = buckets.get(bId); //当某个基数范围内的元素值不存在时，则桶是不存在的，跳过。 if(bk == null){ continue; } Elem[] org = new Elem[bk.size()]; bk.toArray(org); quickSort(org, 0, bk.size() - 1); //将排序后的数据映射到原始数组中作为输出 for(int n=0; n<org.length; n++){ src[stPos++] = org[n]; } } } } /** * 采用类似两边夹逼的方式，向输入数组的中间某个位置夹逼，将原输入数组进行分割成两部分，左边的部分全都小于某个值， * 右边的部分全都大于某个值。 * * 快排算法的核心部分。 * * @param src 待排序数组 * @param start 数组的起点索引 * @param end 数组的终点索引 * @return 中值索引 */ private static int middle(Elem src[], int start, int end){ int middleValue = src[start].getData(); Elem mv = src[start]; while(start < end){ //找到右半部分都比middleValue大的分界点 while(src[end].getData() >= middleValue && start < end){ end--; } //当遇到比middleValue小的时候或者start不再小于end，将比较的起点值替换为新的最小值起点 src[start] = src[end]; //找到左半部分都比middleValue小的分界点 while(src[start].getData() <= middleValue && start < end){ start++; } //当遇到比middleValue大的时候或者start不再小于end，将比较的起点值替换为新的终值起点 src[end] = src[start]; } //当找到了分界点后，将比较的中值进行交换，将中值放在start与end之间的分界点上，完成一次对原数组分解，左边都小于middleValue，右边都大于middleValue src[start] = mv; return start; } /** * 通过递归的方式，对原始输入数组，进行快速排序。 * * @param src 待排序的数组 * @param st 数组的起点索引 * @param nd 数组的终点索引 */ public static void quickSort(Elem src[], int st, int nd){ if(st > nd){ return; } int middleIdx = middle(src, st, nd); //将分隔后的数组左边部分进行快排 quickSort(src, st, middleIdx - 1); //将分隔后的数组右半部分进行快排 quickSort(src, middleIdx + 1, nd); } /** * 打印最终的输出结果 * * @param idx 测试例的编号 * @param B 待输出数组 */ private static void printResult(int idx, Elem B[]){ System.out.print(idx + "--> "); for(int i=0; i<B.length; i++){ System.out.print(B[i].getData() + " "); } System.out.println(); } }
下面附上测试例数据，即sample.txt的内容：
3 11 10 103 202 90 78 13 31 46 57 70 3 24 11 10 24 3 70 57 46 31 13 78 90 202 103 18 10 99 290 87 17 1032 22219 2 13 32 33 219 88 76 85 2017 1982 10 2015
其中，第一组测试例数据，就是本博文中的例题待排序数据。
下面附上测试例对应的结果：
0--> 3 13 24 31 46 57 70 78 90 103 202 1--> 3 13 24 31 46 57 70 78 90 103 202 2--> 2 10 13 17 32 33 76 85 87 88 99 219 290 1032 1982 2015 2017 22219
代码源码中，红色部分，分别指出对应的实现步骤中的第几步，其中，代码中没有反应出实现步骤的第一步，其实这第一步往往是问题思考过程中确定算法方案时，定义的。第一步会影响到后面几步的具体实施细节。
【说明】： 本代码实现，处理的数据，只能是非负数，要想其也能支持负数，需要在基数选取上做下修改，比如将10改成20，相应的改动及实现，读者自己可以思考
基数排序的速度还是很快的，也是一种用空间换时间的策略，因为基数排序，要额外开辟rd（基数）个桶，而桶排序的每个子排序（对每个桶的排序）时间，是有些许不同的，依赖于子排序的算法，上述代码实现中，采用的是快速排序。
基数排序的时间是近乎线性的(请参照桶排序博文)。，基数排序所需的辅助存储空间为 O(n+rd)。
