排序算法<No.3>【桶排序】

算法，是永恒的技能，今天继续算法篇，将研究桶排序。

 

算法思想：

桶排序，其思想非常简单易懂，就是是将一个数据表分割成许多小数据集，每个数据集对应于一个新的集合（也就是所谓的桶bucket），然后每个bucket各自排序，或用不同的排序算法，或者递归的使用bucket sort算法，往往采用快速排序。是一个典型的divide-and-conquer分而治之的策略。

 

其中核心思想在于如何将原始待排序的数据划分到不同的桶中，也就是数据映射过程f(x)的定义，这个f(x)关乎桶数据的平衡性（各个桶内的数据尽量数量不要差异太大），也关乎桶排序能处理的数据类型（整形，浮点型；只能正数，或者正负数都可以）

 

另外，桶排序的具体实现，需要考虑实际的应用场景，因为很难找到一个通吃天下的f(x)。

 

基本实现步骤：

1. 根据数据类型，定义数据映射函数f(x)

2. 对数据进行分别规划进入桶内

3. 对桶做基于序号的排序

4. 对每个桶内的数据进行排序（快排或者其他排序算法）

5. 将排序后的数据映射到原始输入数组中，作为输出

 

桶排序，通常情况下速度非常快，比快速排序还要快，但是，依据我的理解，这个快，应该是建立在大数据量的排序。若待排序的数据元素个数比较少，桶排序的优势就不是那么明显了，因为桶排序就是基于分而治之的策略，可以将数据进行分布式排序，充分发挥并行计算的优势。

 

特性说明：

1. 桶排序的时间复杂度通常是O(N+N*logM)，其中，N表示桶的个数，M表示桶内元素的个数（这里，M取的是一个大概的平均数，这也说明，为何桶内的元素尽量不要出现有的很多，有的很少这种分布不均的事情，分布不均的话，算法的性能优势就不能最大发挥）。

2. 桶排序是稳定的（是可以做到平衡排序的）。

3. 桶排序，在内存方面消耗是比较大的，可以说其时间性能优势是由牺牲空间换来的。

 

下面，我们直接上代码，我的实现过程中，考虑了数据的重复性，考虑到了数据有正有负的情况！

/**
 * @author "shihuc"
 * @date   2017年1月17日
 */
package bucketSort;

import java.io.File;
import java.io.FileNotFoundException;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.Scanner;

/**
 * @author shihuc
 * 
 * 桶排序的实现过程，算法中考虑到了元素的重复性
 */
public class BucketSortDemo {
    
    /**
     * @param args
     */
    public static void main(String[] args) {
        File file = new File("./src/bucketSort/sample.txt");
        Scanner sc = null;
        try {
            sc = new Scanner(file);
            //获取测试例的个数
            int T = sc.nextInt();
            for(int i=0; i<T; i++){
                //获取每个测试例的元素个数
                int N = sc.nextInt();
                //获取桶的个数
                int M = sc.nextInt();                                
                int A[] = new int[N];
                for(int j=0; j<N; j++){
                    A[j] = sc.nextInt();
                }    
                bucketSort(A, M);
                printResult(i, A);
            }
        } catch (FileNotFoundException e) {            
            e.printStackTrace();
        } finally {
            if(sc != null){
                sc.close();
            }
        }
    }
    
    /**
     * 计算输入元素经过桶的个数（M）求商运算后，存入那个桶中，得到桶的下标索引。
     * 步骤1
     * 注意：
     * 这个方法，其实就是桶排序中的相对核心的部分，也就是常说的待排序数组与桶之间的映射规则f（x）的定义部分。 
     * 这个映射规则，对于桶排序算法的不同实现版本，规则函数不同。
     * 
     * @param elem 原始输入数组中的元素值
     * @param m 桶的商数（影响桶的个数）
     * @return 桶的索引号（编号）
     */
    private static int getBucketIndex(int elem, int m){        
        return elem / m;
    }
    
    private static void bucketSort(int src[], int m){
        //定义一个初步排序的桶与原始数据大小的映射关系
        HashMap<Integer, ArrayList<Integer>> buckets = new HashMap<Integer, ArrayList<Integer>>();
        
        //规划数据入桶  【步骤2】              
        programBuckets(src, m, buckets);
        
        //对桶基于桶的标号进行排序（序号可能是负数）【步骤3】
        Integer bkIdx[] = new Integer[buckets.keySet().size()];
        buckets.keySet().toArray(bkIdx);
        quickSort(bkIdx, 0, bkIdx.length - 1);
        
        //计算每个桶对应于输出数组空间的其实位置
        HashMap<Integer, Integer> bucketIdxPosMap = new HashMap<Integer, Integer>();
        int startPos = 0;
        for(Integer idx: bkIdx){
            bucketIdxPosMap.put(idx, startPos);
            startPos += buckets.get(idx).size();
        }
        
        //对桶内的数据采取快速排序,并将排序后的结果映射到原始数组中作为输出
        for(Integer bId : buckets.keySet()){
            ArrayList<Integer> bk = buckets.get(bId);
            Integer[] org = new Integer[bk.size()];
            bk.toArray(org);            
            quickSort(org, 0, bk.size() - 1); //对桶内数据进行排序 【步骤4】
            //将排序后的数据映射到原始数组中作为输出 【步骤5】
            int stPos = bucketIdxPosMap.get(bId); 
            for(int i=0; i<org.length; i++){
                src[stPos++] = org[i];
            }
        }        
    }
    
    /**
     * 基于原始数据和桶的个数，对数据进行入桶规划。
     * 
     * 这个过程，就体现了divide-and-conquer的思想
     * 
     * @param src
     * @param m
     * @param buckets
     */
    private static void programBuckets(int[] src, int m, HashMap<Integer, ArrayList<Integer>> buckets) {
        for(int i=0; i<src.length; i++){
            int bucketIdx = getBucketIndex(src[i], m);
            
            ArrayList<Integer> bucket = buckets.get(bucketIdx);
            if(bucket == null){
                //定义桶，用来存放初步划分好的原始数据
                bucket = new ArrayList<Integer>();
                buckets.put(bucketIdx, bucket);
            }
            bucket.add(src[i]);
        }
    }
    
    /**
     * 采用类似两边夹逼的方式，向输入数组的中间某个位置夹逼，将原输入数组进行分割成两部分，左边的部分全都小于某个值，
     * 右边的部分全都大于某个值。
     * 
     * 快排算法的核心部分。
     * 
     * @param src 待排序数组
     * @param start 数组的起点索引
     * @param end 数组的终点索引
     * @return 中值索引
     */
    private static int middle(Integer src[], int start, int end){
        int middleValue = src[start];
        while(start < end){
            //找到右半部分都比middleValue大的分界点
            while(src[end] >= middleValue && start < end){
                end--;
            }
            //当遇到比middleValue小的时候或者start不再小于end，将比较的起点值替换为新的最小值起点            
            src[start] = src[end];            
            //找到左半部分都比middleValue小的分界点
            while(src[start] <= middleValue && start < end){
                start++;
            }
            //当遇到比middleValue大的时候或者start不再小于end，将比较的起点值替换为新的终值起点
            src[end] = src[start];            
        }
        //当找到了分界点后，将比较的中值进行交换，将中值放在start与end之间的分界点上，完成一次对原数组分解，左边都小于middleValue，右边都大于middleValue
        src[start] = middleValue;
        return start;
    }
    
    /**
     * 通过递归的方式，对原始输入数组，进行快速排序。
     * 
     * @param src 待排序的数组
     * @param st 数组的起点索引
     * @param nd 数组的终点索引
     */
    public static void quickSort(Integer src[], int st, int nd){
        
        if(st > nd){
            return;
        }
        int middleIdx = middle(src, st, nd);
        //将分隔后的数组左边部分进行快排
        quickSort(src, st, middleIdx - 1);
        //将分隔后的数组右半部分进行快排
        quickSort(src, middleIdx + 1, nd);
    }

    /**
     * 打印最终的输出结果
     * 
     * @param idx 测试例的编号
     * @param B 待输出数组
     */
    private static void printResult(int idx, int B[]){
        System.out.print(idx + "--> ");
        for(int i=0; i<B.length; i++){
            System.out.print(B[i] + "  ");
        }
        System.out.println();
    }
}

 

下面附上测试用到的数据：

3
9 2
2 3 1 4 6 -10 8 11 -21
15 5
2 6 3 4 5 10 9 21 17 31 1 2 21 11 18
9 4
2 3 1 4 6 -10 8 11 -21

上面第1行表示有几个测试案例，第二行表示第一个测试案例的熟悉数据，15表示案例元素个数，5表示桶商数（对参与排序的桶的个数有影响）。第3行表示第一个测试案例的待排序数据，第4第5行参照第2和第3行理解。

 

运行的结果如下：

0--> -21  -10  1  2  3  4  6  8  11  
1--> 1  2  2  3  4  5  6  9  10  11  17  18  21  21  31  
2--> -21  -10  1  2  3  4  6  8  11

 

下面附上一个上述测试案例中的一个，通过图示展示算法逻辑

 

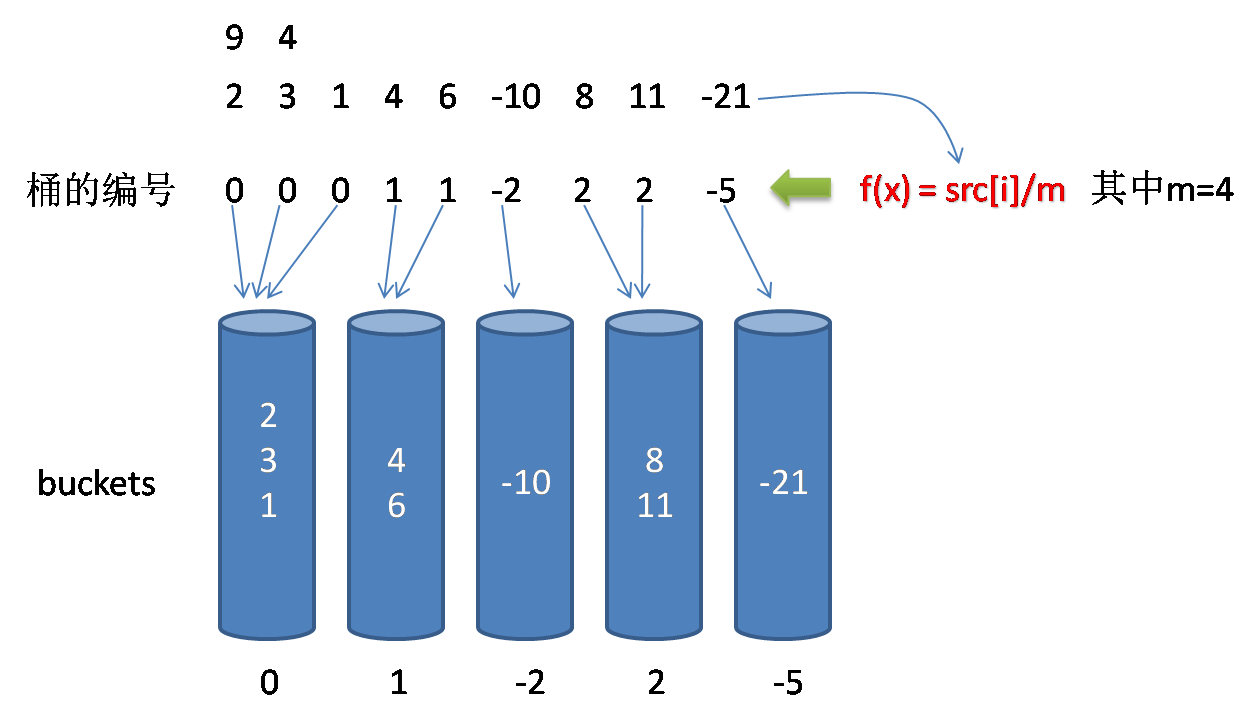
上述算法实现过程中，桶的个数没有直接指定，是有桶的商数决定的。当然，也可以根据实际场景，指定桶的个数，与此同时，算法的实现过程就要做相应的修改，但是整体的思想是没有什么本质差别的。

桶排序，其优势在于处理大数据量的排序场景，数据相对比较集中，这样性能优势很明显。