Largest Rectangle in Histogram

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

 

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

 

 

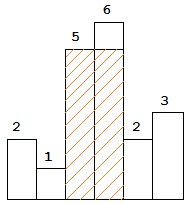
The largest rectangle is shown in the shaded area, which has area = 10 unit.

 

For example,
Given heights = [2,1,5,6,2,3],
return 10.

一道非常经典的题目，一个月前看这道题目不明就里，怎么也想不明白，原来是因为不会使用单调栈这种数据结构。

单调栈是一种栈结构，其中的元素是单调递增，或者单调递减的。单调栈主要用来求一个数左边和右边第一个比他大，或者左边和右边第一个比它小的数。

对于单调递增的栈，可以使用它方便求的一个元素左边第一个比它小的数和右边第一个比它小的数(第一个是指index紧挨着的意思）。

对于单调递减的栈，可以使用它方便求的一个元素左边第一个比它大的数和右边第一个比它大的数(第一个是指index紧挨着的意思）。

对于这道题，brute force的解法是遍历所有左边开始bar，右边结束bar，在这中间查找成为瓶颈的也是就是最低值的bar。复杂度为O(n^3),本身已经是多项式时间的复杂度，使用DP可能性不是很大(??)。换个角度思考一下问题，如果我们不是找边界，而是找瓶颈呢。也就是对每个bar，求以其为瓶颈的一段面积。即这个bar是围成面积的bar中高度最低的那个。如何确定对每个bar，确定这个边界呢，一个显然的办法是查找该bar左边第一个比它小的，右边第一个比它小的，这二者中间就是可以和这个bar围成面积的一段(中间的每个bar都比原来要高）。从这个思路可以看出来使用单调递增栈是一个非常好的选择。

举一个例子，对于题目中给出的例子[2,1,5,6,2,3]：

i ＝ 0， stack = [] , 给栈内增加元素。

i ＝ 1， stack = [index(2)], 1 小于2，则已经已经找到比右边2小的第一个数。 pop(2), 此时栈为空，说明左边没有元素或者所有元素都比它大(不然还在栈内），

           可以从2向左一直计算,此时以2为bottom的面积为2.最后加入1的index

i ＝2，  stack = [index(1)], 加入5的index

i =3,    stack = [index(1), index(5)], 加入6的index

i =4,   stack = [index(1), index(5), index(6)],显然2小于栈顶6，弹出6，则可以对于6求以它为bottom的面积，左边比它小，右边也比它小，所以是4-2-1 ＝ 1（左右index差减1）。面积为6.

         对于5来说，2同样是它右边第一个比它小的元素，所以弹出5，计算面积，w = 4-1-1=2,面积是2*5 ＝ 10。

        此时栈内1比它小，所以压入2 的index

i = 5, stack = [index(1), index(2)], 3 大于栈顶，则加入3的index，栈为［index(1), index(2), index(3)]。

可以看到此时已经到了数组的最后，但是因为一直单调递增，数字无法出栈计算面积。此时栈内元素找不到右边第一个比它小的元素，为了保证计算的正确性，我们显然可以假设右边第一个比它小的元素是 －1，比数组的最小值小的数， 这个数位于len(nums), 这是一个辅助计算的元素值。可以看到它不包含在面积计算中不影响正确性。

使用单调栈，注意元素相等时应该怎么处理，对于这题元素相等同样pop栈内元素，可以看到这样，被pop的bar面积不对。但是对于连续相等的bar，它们中最后一个bar的面积是对的，不影响最后的正确性结果。时间复杂度是O(n)。因为所有元素都进栈和出栈一次，空间复杂度为O(n),最差是连续递增的。代码如下：

         

 

class Solution(object):
    def largestRectangleArea(self, heights):
        """
        :type heights: List[int]
        :rtype: int
        """
        if not heights:
            return 0
        
        #monotonous stack for each bar, find the area that use this bar as bottom, while meet coutinous bars that have same height,         #the area for these bars are not right except the last bar.
        stack = []
        maxArea = 0
        for i in xrange(len(heights)+1): #while i = len(height) this is used for the ramained element in stack while ends
            curt = heights[i] if i < len(heights) else -1
            while (stack and curt <= heights[stack[-1]]): 
                h = heights[stack.pop()]  #caculate area that use this bar as bottom.
                w = i - stack[-1] - 1 if stack else i #while caculate this bar and the stack is empty means that all the 
                                                      #bar before this bar is higher than it. get all the height
                
                maxArea = max(maxArea, h*w)
            stack.append(i)
        return maxArea