bundle adjustment原理(1)
那些光束平差的工具，比如SBA、SSBA之类的虽然好，然而例子和教程都不够多且不够详细，让初学者难以上手。
要传入的参数虽然有解释，然而却也不是十分清楚其含义，具体要怎么生成，生成为什么形式。
我在折腾了一段时间后也还是没成功，逼得我自己找这方面的资料学习，想要更了解bundle adjustment的原理。
想着干脆自己写一个简单的bundle框架练练手，就算写不成也将有助于让这些工具正常工作起来。
三维重建的最后一步是光束平差，又称bundle adjustment，本文介绍一下bundle adjustment的数学原理。
主要是参考 https://www.coursera.org/learn/robotics-perception/home/welcome 第4周里头的内容。
本文做一些数学上的推导以及将资料中的各种公式的含义细化。
自己在推导过程中发现了上述课程ppt中的一些细节地方的公式有错。
2016-09-07 10:24:33
除了上面的资料外，还参考了另一篇文献 “SBA: A Software Package for Generic Sparse Bundle Adjustment”，在bundle adjustment的wiki下以及MATLAB R2016a自带的bundleAdjustment函数中都参考了这篇文献。这篇文献和上述课程ppt中的变量设置略有不同，但大体框架是一样的。
整个 bundle adjustment 的目标是重投影误差最小，所以可以分为两个部分：
1，将某个误差函数的值最小化。这是一个最优化问题，用的是L-M算法。我已经写了一篇L-M算法的博客。
2，将重投影误差的误差函数的具体表达式写出来，套到上面的L-M算法里头去。
假设读者已经有一些最优化的知识。
先从只有1个点、1个相机讲起：
2个摄像机1个点的情况：
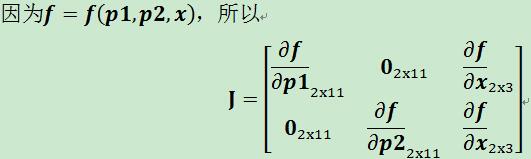
2个摄像机2个点的情况：
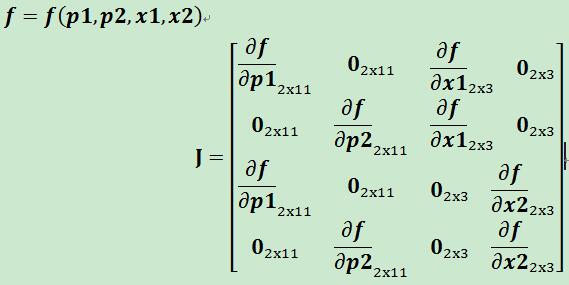
假如有3个摄像机，4个点，则J的大致情形如下，里头的含义模仿上面很容易搞清楚：
对于列来讲，前面3列对应着3个摄像机的变量，后面4列对应着4个点的变量。
那么函数f对变量p和x的偏导怎么求？只有用MATLAB的符号推导才能搞出来，手算非常容易出错
MATLAB代码如下：
被调用的函数sym_mat:
function rtn = sym_mat(x,m,n)
% 生成符号矩阵，第一个参数是一个符号，后面两个参数是符号矩阵的尺寸
% 如果你想生成符号矩阵[x11 x12; x21 x22]只需输入sym_mat(x,2,2)
% 但事先要先声明符号x,用syms x
% 如果你只需要生成一维矩阵，sym_mat会生成一个列向量,如sym_mat(x,2);
% 例子：
% syms x;
% A = sym_mat(x,3,4) 返回一个3 x 4的符号矩阵
if nargin == 2
for i=1:m
rtn(i)=sym([inputname(1),num2str(i)]);
end
rtn = rtn.';
elseif nargin == 3
for i = 1:m
for j = 1:n
rtn(i,j) = sym([inputname(1),num2str(i),num2str(j)]);
end
end
end
符号推导部分：
clear all;clc;close all;
syms P;
P = sym_mat(P,3,4);
P(3,4) = 1
P_var = symvar(P)
syms X;
X = [sym_mat(X,3);
1]
X_var = symvar(X)
uvw = P*X;
u = uvw(1,:);
v = uvw(2,:);
w = uvw(3,:);
f = ...
[u/w;
v/w];
f_P = jacobian(f,P_var)
f_X = jacobian(f,X_var)
J = [f_P f_X]
sym_in_J = symvar(J)
f_P 代表函数 f 对 P 求导，得到 2 x 11 的矩阵
f_X 代表函数 f 对 X 求导，得到 2 x 3 的矩阵
结果很复杂，就不贴出来了。
具体计算矩阵J的值的时候，把变量替换成相应的值就可以了，MATLAB中有subs函数，如果用c++写，
则要自己写一个函数，把值传进去算矩阵J的值。
对于多点多相机的矩阵J，计算不同部分的 f_P 和 f_X，然后把它们组装成一个大的矩阵即可。
先写到这里。。。
2016年9月9日21:50:17
