数论随记(二)


10. 公式
1. a![]() b(mod m)
b(mod m) ![]() (a mod m)
(a mod m) ![]() b (mod m) (化简);
b (mod m) (化简);
HDU1395 (2^x![]() 1(mod n)
1(mod n) ![]() 2^x%n
2^x%n![]() 1(mod n) )
1(mod n) )
3. x![]() n-a(mod m)
n-a(mod m) ![]() x+a
x+a![]() n(mod m); HDU1788
n(mod m); HDU1788
5. a%k=![]() (变型:
(变型: ![]() %k=
%k=![]() ) HDU1852
) HDU1852
如果m与k互素,则(a/m)%k=a*m^(phi(k)-1)%k
6. a≡b(mod m),c≡d(mod m)![]() a±c≡b±d(mod m)
a±c≡b±d(mod m)![]() ac≡bd(mod m)
ac≡bd(mod m)
11. 容斥原理
12. 莫比乌斯反演
反演公式:
其中,
|| 性
13. 规律
n=(a+1)(b+1)-1=(a1+1)(a2+1)(b1+1)(b2+1)-1=…=(a1+1)(a2+1)(a3+1)…(![]() +1)-1
+1)-1
2.
14. 快速幂取模
二分思想,秦九昭算法
typedef long long LL; LL quick_mod(LL a,LL b,LL k) { LL ans=1; while(b>0) { if(b&1) { ans=ans*a%k; } a=a*a%k; b>>=1; } return ans; }
15. 数论四大定理
1.威尔逊定理
若p为质数,则p可整除(p-1)!+1。
2. 欧拉定理
若gcd(a,n) = 1,则a^φ(n) ≡ 1 (mod n)
3. 费马小定理
p是质数,若p不能整除a,则 a^(p-1) ≡1(mod p),
若p能整除a,则a^(p-1) ≡0(mod p)。
(伪素数)满足公式但P非质数。若n能整除2^(n-1)-1,并n是非偶数的合数,那么n就是伪素数。HDU1905
(卡米切尔数) 对于合数n,如果对于所有正整数b,b和n互素,都有同余式b^(n-1)≡ 1 (mod n)成立,则合数n为Carmichael数。
4.中国剩余定理
见9.
16. 矩阵
不满足交换律
2.转置
17. 高斯消元


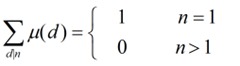
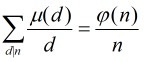
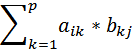

 浙公网安备 33010602011771号
浙公网安备 33010602011771号