队列的实现与应用

队列是一种线性集合，其元素一端加入，从另一端删除，因此我们说队列元素是按先进先出（FIFO）方式处理。

队列的处理过程：通常队列会画成水平，其中一端作为队列的前端（front）也称队首（head）,另一端作为队列的末端（rear）也称队尾（tail）.元素都是从队列末端进入，从队列前端退出.

因而在队列中，其处理过程可在队列的两端进行，而在栈中，其处理过程只在栈的一端进行，但两者也有相似之处，与栈类似，队列中也没有操作能让用户“抵达”队列中部，同样也没有操作允许用户重组或删除多个元素。（不过这些操作都可以再链表中实现）

下面我们定义一个泛型QueueADT接口来表示队列的各种操作（队列的首要作用是保存顺序，而栈则相反是用来颠倒顺序）

package xidian.sl.queue;

import xidian.sl.stack.EmptyCollectionException;

/**
 * 栈的首要作用是颠倒顺序，而队列的首要作用是保持顺序
 * */
public interface QueueADT<T> {
    /*向队列末尾添加一个元素*/
    public void enqueue(T element);
    
    /*从队列前端删除一个元素*/
    public T dequeue() throws EmptyCollectionException;
    
    /*考察队列前端的那个元素*/
    public T first();
    
    /*判断队列是否为空*/
    public boolean isEmpty();
    
    /*判定队列中的元素个数*/
    public int size();
    
    /*返回队列的字符串表示*/
    public String toString();
}

 

与栈的实现一样，我们这里也提供两种实现方法：链表与数组的实现

1.链表实现队列：

队列与栈的区别在于，我们必须要操作链表的两端。因此，除了一个指向链表首元素的引用外，还需要跟踪另一个指向链表末元素的引用。再增加一个整形变量count来跟踪队列中的元素个数。

综合考虑，我们使用末端入列，前端出列

package xidian.sl.queue;

import xidian.sl.stack.EmptyCollectionException;
import xidian.sl.stack.LinearNode;

public class LinkedQueue<T> implements QueueADT<T> {
    //跟踪队列中的元素个数
    private int count;
    //指向首元素末元素的引用
    private LinearNode<T> front, rear;
    
    public LinkedQueue(){
        count = 0;
        front = rear = null;
    }
    
    /**
     * 实现dequeue操作时，确保至少存在一个可返回的元素，如果没有，就要抛出异常
     * @throws EmptyCollectionException 
     * */
    public T dequeue() throws EmptyCollectionException {
        if(isEmpty()){
            throw new EmptyCollectionException("queue");
        }
        
        T result = front.getElement();
        front = front.getNext();
        count--;
        //如果此时队列为空，则要将rear引用设置为null,front也为null，但由于front设置为链表的next引用，已经有处理
        if(isEmpty()){
            rear = null;
        }
        return result;
    }

    /**
     * enqueue操作要求将新元素放到链表的末端
     * 一般情况下，将当前某元素的next引用设置为指向这个新元素，并重新把rear引用设置为指向这个新添加的末元素，但是，如果队列
     * 目前为空，则front引用也要设置为指向这个新元素
     * */
    public void enqueue(T element) {
        LinearNode<T> node = new LinearNode<T>(element);
        
        if(isEmpty()){
            front = node;
        }else{
            rear.setNext(node);
        }
        rear = node;
        count++;
    }

    @Override
    public T first() {
        T result = front.getElement();
        return result;
    }

    @Override
    public boolean isEmpty() {
        return count == 0 ? true : false;
    }

    @Override
    public int size() {
        return count;
    }

}

这里使用到的LinearNode类与在栈中使用到的是一样的：

package xidian.sl.stack;

/**
 * 节点类，含有另个引用，一个指向链表的下一个LinearNode<T>节点，
 * 另一个指定本节点中存储的元素 
 * */
public class LinearNode<T> {
    /*指向下一个节点*/
    private LinearNode<T> next;
    /*本节点存储的元素*/
    private T element;
    
    /*创建一个空的节点*/
    public LinearNode(){
        next = null;
        element = null;
    }
    
    /*创建一个存储了特殊元素的节点*/
    public LinearNode(T elem){
        next = null;
        element = elem;
    }
    
    /*返回下一个节点*/
    public LinearNode<T> getNext(){
        return next;
    }
    
    /*设置下一个节点*/
    public void setNext(LinearNode<T> node){
        next = node;
    }

    /*获得当前节点存储的元素*/
    public T getElement() {
        return element;
    }
    
    /*设置当前节点存储的元素*/
    public void setElement(T element) {
        this.element = element;
    }
    
    
    
}

 

2.数组实现队列：

固定数组的实现在栈中是很高效的，是因为所有的操作（增删等）都是在集合的一端进行的，因而也是在数组的一端进行的，但在队列的实现中则不是这样，因为我们是在两端对队列进行操作的，因此固定数组的实现效率不高。

分析：1.将队列的首元素总是存储在数组的索引0处，由于队列处理会影响到集合的两端，因此从队列中删除元素的时候，该策略要求移动元素，这样操作的效率就很低

2.如果将队列的末端总是存储在数组索引0处，当一个元素要入列时，是在末端进行操作的，这就意味着，每个enqueue操作都会使得队列中的所有元素在数组中移动一位，效率仍然很低。

3.如果不固定在哪一端，当元素出列时，队列的前端在数组中前移，当元素入列时，队列的末端也在数组中前移，当队列的末端到达了数组的末端将出现难题，此时加大数组容量是不切合实际的，因为这样将不能有效的利用数组的空闲空间。

因此我们的解决方法是将数组看作是环形（环形数组）的，这样就可以除去在队列的数组实现，环形数组并不是一种新的结构，它只是一种把数组用来存储队列的方法，环形数组即数组的最后一个索引后面跟的是第一个索引。

实现方案：用两个整数值来表示队列的前端和末端，当添加和删除元素时，这些值会改变。注意，front的值表示的是队列首元素存储的位置，rear的值表示的是数组的下一个可用单元（不是最后一个元素的存储位置），而由于rear的值不在表示队列的元素数目，因此我们需要使用一个单独的整数值来跟踪元素计数。

由于使用环形数组，当队列的末端到达数组的末端时，它将“环绕”到数组的前端，因此，队列的元素可以跨越数组的末端。

package xidian.sl.queue;

import xidian.sl.stack.EmptyCollectionException;

public class CircularArrayQueue<T> implements QueueADT<T>{
    //数组的默认容量大小
    private final int DEFAULT_CAPACITY = 100;
    private int front, rear, count;
    private T[] queue;
    
    @SuppressWarnings("unchecked")
    public CircularArrayQueue(){
        front = rear = count = 0;
        queue = (T[]) new Object[DEFAULT_CAPACITY];
    }
    
    @SuppressWarnings("unchecked")
    public CircularArrayQueue(int initialCapacity){
        front = rear = count = 0;
        queue = (T[]) new Object[initialCapacity];
    }
    
    /**
     * 一个元素出列后，front的值要递减，进行足够的dequeue操作后，front的值将到达数组的最后一个索引处，当最大索引处的元素被
     * 删除后，front的值必须设置为0而不是递减，在enqueue操作中用于设置rear值的计算，也可以用来设置dequeue操作的front值
     * */
    public T dequeue() throws EmptyCollectionException {
        if(isEmpty()){
            throw new EmptyCollectionException("queue");
        }
        T result = queue[front];
        queue[rear] = null;
        front = (front + 1) % queue.length;
        count--;
        return result;
    }

    /**
     * enqueue操作：通常，一个元素入列后，rear的值要递增，但当enqueue操作填充了数组的最后一个单元时，
     * rear必须设为0，表面下一个元素应该存储在索引0处，下面给出计算rear值的公式：
     * rear = （rear + 1） % queue.length;（queue是存储队列的数组名）
     * */
    public void enqueue(T element) {
        //首先查看容量，必要时进行扩容
        if(size() == queue.length){
            expandCapacity();
        }
        queue[rear] = element;
        rear = (rear + 1) % queue.length;
        count++;
    }

    @Override
    public T first() throws EmptyCollectionException {
        if(isEmpty()){
            throw new EmptyCollectionException("queue");
        }
        return queue[front];
    }

    @Override
    public boolean isEmpty() {
        return count == 0 ? true : false;
    }

    @Override
    public int size() {
        return count;
    }
    
    /**
     * 当数组中的所有单元都已填充，就需要进行扩容，
     * 注意：已有数组的元素必须按其在队列中的正确顺序（而不是它们在数组中的顺序）复制到新数组中
     * */
    @SuppressWarnings("unchecked")
    private void expandCapacity(){
        //增加为原容量的2倍
        T[] larger = (T[]) new Object[queue.length*2];
        //新数组中从索引0处开始按队列的正确顺序进行填充元素
        for(int scan = 0; scan < count; scan++){
            larger[scan] = queue[front];
            front = (front + 1) % queue.length;
        }
        //重新定位front,rear,queue
        front = 0;
        rear = count;
        queue = larger;
    }
}

队列的应用实例：

1.代码密钥：凯撒加密法是一种简单的消息编码方式，它是按照字母表将消息中的每个字母移动常量的k位，但这种方式极易破解，因为字母的移动只有26种可能。

因此我们使用重复密钥：这是不是将每个字母移动常数位，而是利用一个密钥值列表，将各个字母移动不同的位数。如果消息比密钥值长，可以从头再使用这个密钥值列表；

package xidian.sl.queue;

import xidian.sl.stack.EmptyCollectionException;

public class Codes {
    public static void main(String[] args) throws EmptyCollectionException {
        //消息的密钥
        int[] key = {5, 12, -3, 8, -9, 4, 10};
        Integer keyValue;
        String enCoded = "", deCoded = "";
        //待加密的字符串
        String message = "All programmers are playWrights and all computers are lousy actors";
        //用于存储密钥的队列
        CircularArrayQueue<Integer> keyQueue1 = new CircularArrayQueue<Integer>();
        CircularArrayQueue<Integer> keyQueue2 = new CircularArrayQueue<Integer>();
        
        //两个队列分别存储一份密钥，模拟消息编码者使用一份密钥，消息解码者使用一份密钥
        for(int scan = 0; scan < key.length; scan++){
            keyQueue1.enqueue(new Integer(key[scan]));
            keyQueue2.enqueue(new Integer(key[scan]));
        }
        //利用队列存储密钥使得密钥重复很容易，只要在用到每个密钥值后将其放回到队列即可
        for(int scan = 0; scan < message.length(); scan++){
            //取一个密钥
            keyValue = keyQueue1.dequeue();
            //会将该字符移动Unicode字符集的另外一个位置
            enCoded += (char)((int)message.charAt(scan) + keyValue.intValue());
            //将密钥重新存储到队列中
            keyQueue1.enqueue(keyValue);
        }
        System.out.println("Encoded Message:\n"+enCoded+"\n");
        
        for(int scan = 0; scan < enCoded.length(); scan++){
            keyValue = keyQueue2.dequeue();
            deCoded += (char)((int)enCoded.charAt(scan) - keyValue.intValue());
            keyQueue2.enqueue(keyValue);
        }
        System.out.println("Decoded Message:\n"+deCoded);
        
    }
}

运行结果：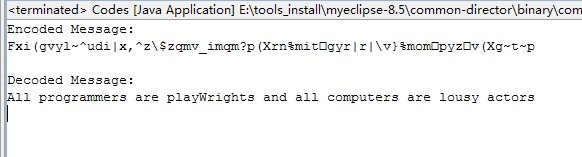

2.利用队列的保存顺序特性，模拟售票口

考虑去银行办业务：一般来说，服务窗口越多，队走的越快，银行经理希望顾客满意，但又不希望雇佣过多的员工。

我们模拟的服务窗口有如下假设：

1.只排一队，并且先到的人先得到服务（这是一个队列）

2.平均每隔15秒就会来一位顾客

3.如果有空闲的窗口，在顾客抵达之时就会马上处理

4.从顾客来到窗口到处理完顾客请求，这个平均需要120秒

以下就来模拟高峰期银行开多少个窗口最为合适：

先模拟一个顾客类：

package xidian.sl.queue;

public class Costomer {
    //arrivalTime跟踪顾客抵达售票口的时间，departureTime跟踪顾客买票后离开售票口的时间
    private int arrivalTime, departureTime;
    
    public Costomer(int arrives){
        arrivalTime = arrives;
        departureTime = 0;
    }

    public int getArrivalTime() {
        return arrivalTime;
    }

    public void setArrivalTime(int arrivalTime) {
        this.arrivalTime = arrivalTime;
    }

    public int getDepartureTime() {
        return departureTime;
    }

    public void setDepartureTime(int departureTime) {
        this.departureTime = departureTime;
    }
    //顾客买票所花的总时间就是离开时间-抵达时间
    public int totalTime(){
        return (departureTime-arrivalTime);
    }
    
}

模拟类：

package xidian.sl.queue;

import xidian.sl.stack.EmptyCollectionException;


public class TicketCounter {
    //接受服务的时间
    private static int PROCESS = 120;
    //最多窗口数
    private static int MAX_CASHIERS = 10;
    //顾客的数量
    private static int NUM_CUSTOMERS = 100;
    
    public static void main(String[] args) throws EmptyCollectionException {
        Costomer costomer;
        //存储顾客的队列
        LinkedQueue<Costomer> costomerQueue = new LinkedQueue<Costomer>();
        int[] cashierTime = new int[MAX_CASHIERS];
        int totalTime, averageTime, departs;
        //该循环决定了每遍模拟时用了多少个售票口
        for(int cashiers = 0; cashiers < MAX_CASHIERS; cashiers++){
            //将售票口的服务时间初始化为 0
            for(int count = 0; count < cashiers; count++){
                cashierTime[count] = 0;
            }
            //往costomerQueue存储顾客，模拟每隔15分钟来一个顾客
            for(int count = 1; count <= NUM_CUSTOMERS; count++){
                costomerQueue.enqueue(new Costomer(count*15));
            }
            //初始化总的服务时间为0
            totalTime = 0;
            //开始服务
            while(!(costomerQueue.isEmpty())){
                for(int count = 0; count <= cashiers; count++){
                    if(!(costomerQueue.isEmpty())){
                        //取出一位顾客
                        costomer = costomerQueue.dequeue();
                        //顾客来的时间与售票口的服务时间相比
                        if(costomer.getArrivalTime() > cashierTime[count]){
                            //表示空闲，可以进行服务
                            departs = costomer.getArrivalTime() + PROCESS;
                        }else{
                            //无空闲则需排队等待
                            departs = cashierTime[count] + PROCESS;
                        }
                        //保存用户的离开时间
                        costomer.setDepartureTime(departs);
                        //设置该售票口的服务时间
                        cashierTime[count] = departs;
                        //计算总的服务时间
                        totalTime += costomer.totalTime();
                    }
                }
            }
            
            averageTime = totalTime / NUM_CUSTOMERS;
            System.out.println("售票口数量： "+(cashiers+1));
            System.out.println("平均时间： "+averageTime+"\n");
            
        }
    }
    
}

模拟结果：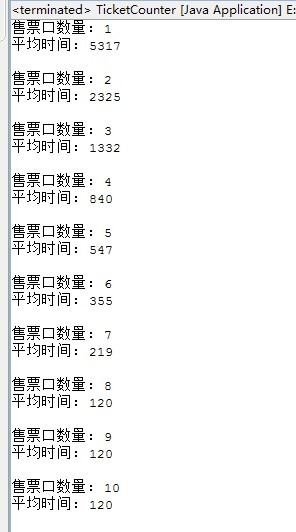

由模拟结果可知最合适是开8个窗口