POJ1942

Paths on a Grid

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 24236		Accepted: 6006

Description

Imagine you are attending your math lesson at school. Once again, you are bored because your teacher tells things that you already mastered years ago (this time he's explaining that (a+b)²=a²+2ab+b²). So you decide to waste your time with drawing modern art instead.

Fortunately you have a piece of squared paper and you choose a rectangle of size n*m on the paper. Let's call this rectangle together with the lines it contains a grid. Starting at the lower left corner of the grid, you move your pencil to the upper right corner, taking care that it stays on the lines and moves only to the right or up. The result is shown on the left:

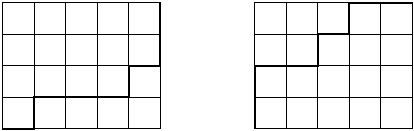
Really a masterpiece, isn't it? Repeating the procedure one more time, you arrive with the picture shown on the right. Now you wonder: how many different works of art can you produce?

Input

The input contains several testcases. Each is specified by two unsigned 32-bit integers n and m, denoting the size of the rectangle. As you can observe, the number of lines of the corresponding grid is one more in each dimension. Input is terminated by n=m=0.

Output

For each test case output on a line the number of different art works that can be generated using the procedure described above. That is, how many paths are there on a grid where each step of the path consists of moving one unit to the right or one unit up? You may safely assume that this number fits into a 32-bit unsigned integer.

Sample Input

5 4
1 1
0 0

Sample Output

126
2

Source

Ulm Local 2002

 

一次又一次的相信自己dp一样可以过，dp优化到了极点.对拍5000以下数据无误，只是数据范围太大，动态申请内存也无效了。

不过没有遗憾，虽然浪费了一个小时，但值得！

WA代码：

#include<cstdio>
#include<iostream>
using namespace std;
long long n,m;
int main(){
    while(scanf("%I64d%I64d",&n,&m)==2){
        if(!n&&!m) break;
        long long **a=new long long *[n+1];
        for(long long i=0;i<=n;i++)
            a[i]=new long long [m+1];
        for(long long i=1;i<=max(n,m);i++) a[i][0]=1,a[0][i]=1;
        for(long long i=1;i<=n;i++)
            for(long long j=1;j<=m;j++)
                a[i][j]=a[i-1][j]+a[i][j-1];
        printf("%.0lf\n",(double)a[n][m]);
        delete a;
    }
    return 0;
}

 

正解思路：用到了组合数学的方法。给出n*m的网格，也就是必须有n个向右走的格子和m个            向上走的格子，加起来是（n+m）步。也就是，给定（m+n）个格子，向上和向         右的数目是一定的，则转化成在（m+n）个格子里面计算出有多少种m个格子各            不相同。

组合数学的基本公式：

由此 result=(n+m)! /  ( m!*n!)

求result的过程：

1： 传统方法进行运算，则会造成超时

2： 最快速的方法是逐级相除，并且把各级所得的结果想乘，最终得到的是一个double         类型的数据（double类型的数据注意四舍五入）

数论版AC代码：

 

#include<iostream>
#include<cstdio>
using namespace std;
int main(){
    long long n,m,i;
    double s,tt;
    //while(scanf("%I64d%I64d",&n,&m)==2&&n&&m){//这样过不了
    while(scanf("%I64d%I64d",&n,&m)==2){
        if(!n&&!m) break;//改成这样才能过
        tt=n+m;
        if(n>m) n=m;
        s=1;
        for(i=1;i<=n;i++)
            s*=(tt-i+1.0)/(i+0.0);
        printf("%.0lf\n",s);
    }
    return 0;
}