2016-06-19 NOIP模拟赛
2016-06-19 NOIP模拟赛
by coolyangzc
共3道题目,时间3小时
|
题目名 |
高级打字机 |
不等数列 |
经营与开发 |
|
源文件 |
type.cpp/c/pas |
num.cpp/c/pas |
exploit.cpp/c/pas |
|
输入文件 |
type.in |
num.in |
exploit.in |
|
输出文件 |
type.out |
num.out |
exploit.out |
|
时间限制 |
1000MS |
1000MS |
1000MS |
|
内存限制 |
256MB |
256MB |
256MB |
|
测试点 |
5+(5) |
10 |
10 |
|
测试点分值 |
20 |
10 |
10 |
评测环境
操作系统:Windows XP SP3
CPU: Pentium(R) Dual-Core CPU E5300 @ 2.60Ghz(2CPUs)
系统内存:2GB
Problem 1 高级打字机(type.cpp/c/pas)
评测地址:http://codevs.cn/problem/3333/
【题目描述】
早苗入手了最新的高级打字机。最新款自然有着与以往不同的功能,那就是它具备撤销功能,厉害吧。
请为这种高级打字机设计一个程序,支持如下3种操作:
1.T x:在文章末尾打下一个小写字母x。(type操作)
2.U x:撤销最后的x次修改操作。(Undo操作)
(注意Query操作并不算修改操作)
3.Q x:询问当前文章中第x个字母并输出。(Query操作)
文章一开始可以视为空串。
【输入格式】
第1行:一个整数n,表示操作数量。
以下n行,每行一个命令。保证输入的命令合法。
【输出格式】
每行输出一个字母,表示Query操作的答案。
【样例输入】
7
T a
T b
T c
Q 2
U 2
T c
Q 2
【样例输出】
b
c
【数据范围】
对于40%的数据 n<=200;
对于100%的数据 n<=100000;保证Undo操作不会撤销Undo操作。
<高级挑战>
对于200%的数据 n<=100000;Undo操作可以撤销Undo操作。
<IOI挑战>
必须使用在线算法完成该题。
题解:
因为Undo操作只能撤销Type操作,所以Undo x 实际上就是删除文章末尾x个字母。用一个栈即可解决(每个字母最多进出一次)。
<高级挑战> (考虑到部分选手水平较高,故设此附加题)
本题虽为2012年IOI的题目,但只要使用离线算法,就成为只需noip级别编程水平的题目了。
以下声明一些定义:(对于此类题目以及各种可持久化数据结构的离线解法的思考很有帮助)
版本:接受第1--i个修改操作(包含Type和Undo)后的状态称为版本i。版本0为初始状态。
版本链:一般的数据结构题目只有各种修改命令(比如本题的Type操作),那么所有版本就会呈链状排列。
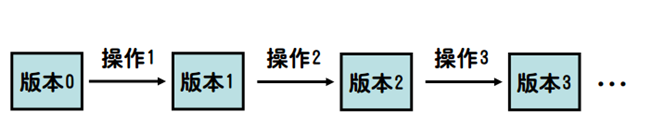
这种情况下只需要设计一个合理的数据结构依次执行操作即可。
版本树:Undo x撤销最近的x次修改操作,实际上就是当前版本还原为x次操作前的版本,换句话说,版本i = 版本i-x-1。
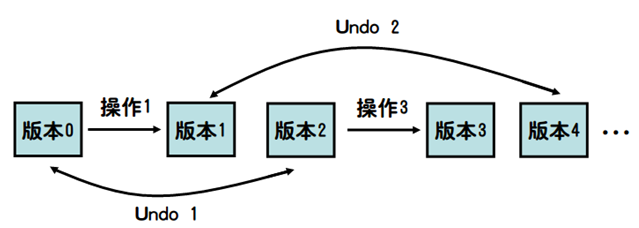
如图所示,所有版本呈树状排列,版本0为根。
读入所有操作并建树,对这颗版本树按欧拉序求出所有版本。上图中就是按0->1->4...4->1->0->2->3->2->0的顺序遍历,同样使用栈就能计算出所有的版本,然后在对应的版本上解决询问即可。
到此,就得到了时空复杂度均为O(n)的离线算法。
能解决这类题目的条件是:
1.允许使用离线算法,进而求出版本树,并允许把询问挂到树的节点上。
2.所有操作都是可逆的。只有所有操作都是可逆的,才能按欧拉序依次求出各版本。如本题的Type操作的逆操作就是弹出栈顶,Undo操作则根本不需要修改(Undo前后2个版本相同)。
相关题目:crisis 60% (2012 国家集训队hw2出题互测\卓亮)
<IOI挑战>
Trie+倍增法寻祖 O(nlogn)
各种可持久化数据结构:可持久化块状数组 O(nsqrtn)
可持久化跳表(与Trie解法相近) O(nlogn)
......
因超出noip范围不做更多展开。
100%的数据
#include<cstdio> #include<iostream> using namespace std; int n,top; char a[1000001]; int main(){ scanf("%d",&n); while(n--){ char ch[10];int x; scanf("%s",ch); if(ch[0]=='T') cin>>a[++top]; else if(ch[0]=='U'){ scanf("%d",&x); top-=x; } else{ scanf("%d",&x); cout<<a[x]<<endl; } } return 0; }
200%的数据
可持续线段树版:
概念理解:http://www.cnblogs.com/shenben/p/5598371.html
#include<cstdio> using namespace std; #define N 2000010 char S[N]; int ToT,root[N/2],len[N/2],ls[N],rs[N]; inline int read() { register int x=0,f=1; register char ch=getchar(); while(ch>'9'||ch<'0'){if(ch=='-') f=-1;ch=getchar();} while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar(); return x*f; } void update(int& y,int x,int l,int r,int pos,char c) { y=++ToT; if(l==r) S[y]=c; else{ int mid=l+r>>1;ls[y]=ls[x];rs[y]=rs[x]; if(pos<=mid) update(ls[y],ls[x],l,mid,pos,c); else update(rs[y],rs[x],mid+1,r,pos,c); } } void query(int y,int l,int r,int pos) { if(l==r) printf("%c\n",S[y]); else{ int mid=l+r>>1; if(pos<=mid) query(ls[y],l,mid,pos); else query(rs[y],mid+1,r,pos); } } int main() { int n=read(),vs=0; while(n--) { char cmd[2],s[2]; scanf("%s",cmd); if(cmd[0]=='T') { scanf("%s",s);vs++;len[vs]=len[vs-1]+1; update(root[vs],root[vs-1],1,100000,len[vs],s[0]); } else if(cmd[0]=='U') { int x=read();vs++; root[vs]=root[vs-x-1]; len[vs]=len[vs-x-1]; } else query(root[vs],1,100000,read()); } return 0; }
都说这是道rope裸题……rope标程:
(然而,我还小~~)
#include<cstdio> #include<iostream> #include<ext/rope> using namespace std; using namespace __gnu_cxx; const int maxn=1e5+10; rope<char> *his[maxn]; int n,m; inline char getC(){ for(register char ch=getchar();;ch=getchar()) if((ch>='A'&&ch<='Z')||(ch>='a'&&ch<='z')) return ch; } inline int getint(){ register int x=0,f=1; register char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int main(){ n=getint(); his[0]=new rope<char>(); for(int i=1;i<=n;i++){ char opt=getC(); if(opt=='T'){ m++; his[m]=new rope<char>(*his[m-1]);//就是这一句!它可以实现O(1)的拷贝历史版本,由于rope的底层是平衡树,copy时copy根节点就行了;用它就可以轻松实现可持久化数组 char x=getC(); his[m]->push_back(x); }else if(opt=='U'){ int x=getint(); m++; his[m]=new rope<char>(*his[m-x-1]); }else if(opt=='Q'){ int x=getint()-1; putchar(his[m]->at(x)); putchar('\n'); } } return 0; }
Problem 2 不等数列(num.cpp/c/pas)
评测地址:http://codevs.cn/problem/4357/
【题目描述】
将1到n任意排列,然后在排列的每两个数之间根据他们的大小关系插入“>”和“<”。问在所有排列中,有多少个排列恰好有k个“<”。答案对2012取模。
【输入格式】
第一行2个整数n,k。
【输出格式】
一个整数表示答案。
【样例输入】
5 2
【样例输出】
66
【数据范围】
对于30%的数据:n <= 10
对于100%的数据:k < n <= 1000,
题解:
对于30% n<=10的数据,搜索打表,状态压缩动态规划......
对于1--n等类似的排列计数问题,以动态规划和组合数学2种大方向为基本解决方向。
组合数学在noip最难也就到杨辉三角左右,所以这题我从动态规划展开。
如果此类排列问题在脑中的模型是:“有n个格子,填入1--n”,那么相对应的DP就不得不记录哪些数填过了(从左到右填入)或者哪些格子填过了(从小到大填入)。这样一来就必须要使用状态压缩来存储这些信息,就使得复杂度变得难以接受。
而如果换个模型:“从小到大把数字插入数列”。注意是数列而不是格子,这样一来就不需要记录是哪些数字插入了(而只要记录插入到了第几个数字),同时不需要记录每个数字的具体位置,也不需要记录数字的相对位置,而只需记录相对关系的数目(对本题而言就是有几个“<”)。
因为是从小到大插入数字,所以当前插入的数字一定大于所有已经插入的。
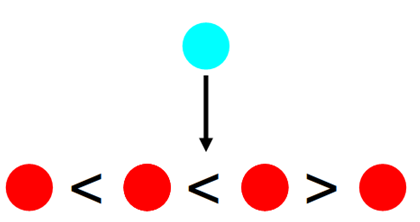
蓝色是当前插入的数字,如果它插入到<关系的2个数字之间(或者数列最左端),就会使数列的<数量不变,>数量+1:
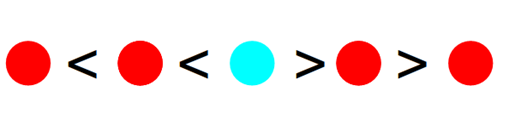
类似的,插入到>关系的2个数字之间(或者数列最右端),数列的<数量+1,>数量不变。
F[i][j]表示前i个数字构成的数列中,恰有j个‘<’号的方案数(‘>’号就有i-j-1个)。
F[i][j]=F[i-1][j-1]*(i-j)+F[i-1][j]*(j+1).
时空复杂度:O(n^2)
若打表则时间复杂度为O(1)
风格1:
#include<cstdio> #include<iostream> using namespace std; #define N 1010 long long f[N][N]; int n,k; int main(){ //freopen("num.in","r",stdin); //freopen("num.out","w",stdout); scanf("%d%d",&n,&k); f[1][0]=1; for(int i=1;i<n;i++){ for(int j=0;j<i;j++){ f[i][j]%=2012; f[i+1][j]+=(j+1)*f[i][j]; f[i+1][j+1]+=(i-j)*f[i][j]; } } printf("%lld",f[n][k]%2012); return 0; }
风格2:
#include<cstdio> #include<iostream> using namespace std; #define N 1010 #define mod 2012 int f[N][N]; int n,k; int main(){ //freopen("num.in","r",stdin); //freopen("num.out","w",stdout); scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) f[i][0]=1; for(int i=1;i<=n;i++) for(int j=1;j<i;j++) f[i][j]=(f[i-1][j]*(j+1)%mod+f[i-1][j-1]*(i-j)%mod)%mod; printf("%d\n",f[n][k]); return 0; }
Problem 3 经营与开发(exploit.cpp/c/pas)
评测地址:http://www.luogu.org/problem/show?pid=1412
【题目描述】
4X概念体系,是指在PC战略游戏中一种相当普及和成熟的系统概念,得名自4个同样以“EX”为开头的英语单词。
eXplore(探索)
eXpand(拓张与发展)
eXploit(经营与开发)
eXterminate(征服)
——维基百科
今次我们着重考虑exploit部分,并将其模型简化:
你驾驶着一台带有钻头(初始能力值w)的飞船,按既定路线依次飞过n个星球。
星球笼统的分为2类:资源型和维修型。(p为钻头当前能力值)
1.资源型:含矿物质量a[i],若选择开采,则得到a[i]*p的金钱,之后钻头损耗k%,即p=p*(1-0.01k)
2.维修型:维护费用b[i],若选择维修,则支付b[i]*p的金钱,之后钻头修复c%,即p=p*(1+0.01c)
注:维修后钻头的能力值可以超过初始值(你可以认为是翻修+升级)
请作为舰长的你仔细抉择以最大化收入。
【输入格式】
第一行4个整数n,k,c,w。
以下n行,每行2个整数type,x。
type为1则代表其为资源型星球,x为其矿物质含量a[i];
type为2则代表其为维修型星球,x为其维护费用b[i];
【输出格式】
一个实数(保留2位小数),表示最大的收入。
【样例输入】
5 50 50 10
1 10
1 20
2 10
2 20
1 30
【样例输出】
375.00
【数据范围】
对于30%的数据 n<=100
另有20%的数据 n<=1000;k=100
对于100%的数据 n<=100000; 0<=k,c,w,a[i],b[i]<=100;保证答案不超过10^9
题解:
“依次飞过n个星球”,第一反应就是动态规划,然后验证下无后效性即可。
这题关键点为状态的设计。
<Method 1>
F[i][x]表示到达第i个星球,且钻头能力值为x的最大收入值。
x因为是实数,所以要取一定的精度。对于数值范围都在100的本题,n在10左右的时候毫无压力。
时空复杂度:O(nx) x为精度范围。
期望得分:10-30;
<Method 2>
F[i][x][y]表示到达第i个星球,且之前开采过x次,维修过y次。
因为本题开采和维修对钻头的影响都是定值。所以钻头能力就是w*k^x*c^y
时空复杂度:O(n^3)
期望得分:30
<Method 3>
对于20% k=100的数据,钻头开采一次就永久损坏了。所以只需记录维修过几次即可。
时空复杂度:O(n^2)
期望得分:20 (配合Method 2为50)
<Method 4>
与Method 2一样的状态设计。但是x,y的范围不需要与n相同。因为在随机情况下,开采和维修的次数寥寥无几(结合次幂考虑)。
时空复杂度:O(nxy) x,y为选手选择的范围
期望得分:30-80
<Method 5>
与Method 2一样的状态设计,但是使用BFS来进行DP过程,这样就不会遍历到没有被访问到的状态,同时选手可以自己加上一些简单的贪心判断来减少状态数量。
时空复杂度:O(?)
期望得分:70-100
<Method 6>
与前5种做法截然不同。前5种做法的最大瓶颈就是“当前钻头能力”,下面我们尝试不存储“当前钻头能力”。
F[i]表示前i个星球的最优收入。很明显这是不行的,因为当前钻头能力会切实影响到后面的过程,不严谨的说,当前钻头能力有“后效性”。
但是这个当前钻头能力对后程的影响无非就是乘上一个数值。(就好像初始钻头能力为w,实际上你可以按1来做,最后再把ans乘上w)。
正难则反,F[i]表示第i--n个星球的最优收入,且假设从第i个星球开始时钻头能力为1。换句话说,这样的状态设计,规定了一个参考系。
转移过程就变得简单:如果在第i个星球开采,那么第i+1--n个星球的初始钻头能力就是1*(1-0.01k)。换句话说,就是F[i+1]*(1-0.01k)。
所以F[i]=max{F[i+1],F[i+1]*(1-0.01k)+a[i]}
对于维护型星球,大同小异。就系数和代价的正负而已。
观察方程,F[i]=max{F[i+1],F[i+1]*(1-0.01k)+a[i]}
实际上就是取下i+1--n的最值而已,所以这题实际上就成了贪心。
#include<cstdio> #include<iostream> using namespace std; #define N 100010 int n,t[N],a[N]; double k,c,w,ans=0; int main(){ //freopen("exploit.in","r",stdin); //freopen("exploit.out","w",stdout); scanf("%d%lf%lf%lf",&n,&k,&c,&w); k=1-0.01*k;c=1+0.01*c;//关键处理 for(int i=1;i<=n;i++) scanf("%d%d",t+i,a+i); for(int i=n;i>=1;i--){ if(t[i]==1) ans=max(ans,ans*k+a[i]); else ans=max(ans,ans*c-a[i]); } printf("%.2lf",ans*w); return 0; }

