计算球面上两点弧长
1,三角形余弦定理
余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与他们夹角的余弦的两倍积,若三边为a,b,c 三角为A,B,C ,则满足性质——
(注:a*b、a*c就是a乘b、a乘c 。a^2、b^2、c^2就是a的平方,b的平方,c的平方。)
a^2=b^2+c^2-2*b*c*CosA
b^2=a^2+c^2-2*a*c*CosB
c^2=a^2+b^2-2*a*b*CosC
CosC=(a^2+b^2-c^2)/2ab
CosB=(a^2+c^2-b^2)/2ac
CosA=(c^2+b^2-a^2)/2bc
平面向量证法
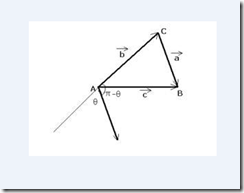
∵如图,有a+b=c (平行四边形定则:两个邻边之间的对角线代表两个邻边大小)∴c·c=(a+b)·(a+b)
∴c^2=a·a+2a·b+b·b∴c^2=a^2+b^2+2|a||b|Cos(π-θ)
(以上粗体字符表示向量)
又∵Cos(π-θ)=-CosC
∴c^2=a^2+b^2-2|a||b|Cosθ(注意:这里用到了三角函数公式)
再拆开,得c^2=a^2+b^2-2*a*b*CosC
同理可证其他,而下面的CosC=(c^2-b^2-a^2)/2ab就是将CosC移到左边表示一下。
2,利用三角形余弦定理求解两点之间的弧度
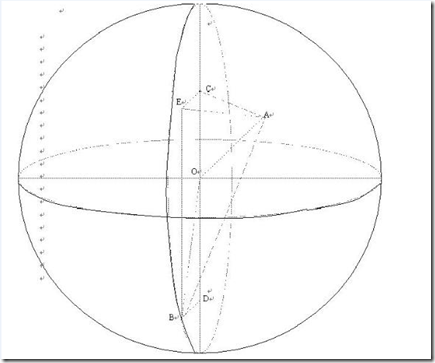
如图,先假设球的半径为R,所给定的2点为A,B两点,先假设A在北半球,B在南半球。(这只是其中的一种情况,至于其它的情况可以同样的方法计算出,仅仅是大同小异而已。当然,还有特殊情况也不能忘了哦。)假设球心为点O,那么最后得到的∠AOB的弧度乘以球的半径R即为所求的球面距离。设经过球的南极和北极的极点的直线为l,分别过点B、A作l的垂线,设垂点分别为D、C。过点B作线BC的平行线BE,过C作BD的平行线CE,这两条平行线必定相交,交点为E,容易证明BDCE是一个矩形,同时,因为BE垂直AC且垂直EC,所以三角形AEB为直角三角形。 由于A、B点的经纬度已知,所以∠OBD和∠OAC也已知,设分别为β,α,由于半径R已知,所以|BD| = R * cosβ,|AC| = R * cosα,|OD| = R * sinβ,|OC| = R * sinα。由于点A、B的经度已知,所以不难求出∠ACE的值。所以三角形ACE中不难用余弦定理求出|AE|的值。在直角三角形ABE中,容易求出AB的值。此时三角形AOB三条边都已知,所以∠AOB也可以用余弦定理求出来。