匈牙利 算法&模板

匈牙利 算法

一. 算法简介

匈牙利算法是由匈牙利数学家Edmonds于1965年提出。该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

二分图的定义：

设G=(V,E)是一个无向图，顶点集V可分割为两个互不相交的子集V1,V2，那么称此图G为二分图。

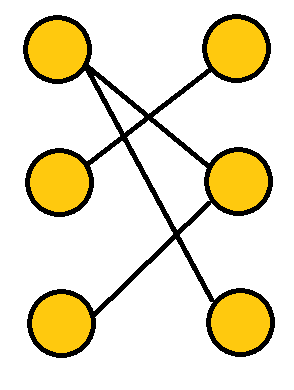
例如，下图就是一个二分图：

二分图的匹配：

二分图中的子图中，每个节点只连一条边，则称该子图是二分图中的一个匹配。

 

极大匹配：

无法再向二分图中加入边，使得满足匹配条件。

 

最大匹配：

所有极大匹配中边数最多的一个匹配。

 

完美匹配：

如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。

 

方法：

求最大匹配的一种显而易见的算法是:先找出全部匹配，然后保留匹配数最多的。但是这个算法的时间复杂度为边数的指数级。因此，需要寻求一种更加高效的算法。下面介绍用增广路求最大匹配的方法。

 

算法图解：

下图是一个二分图，现在求最大匹配。

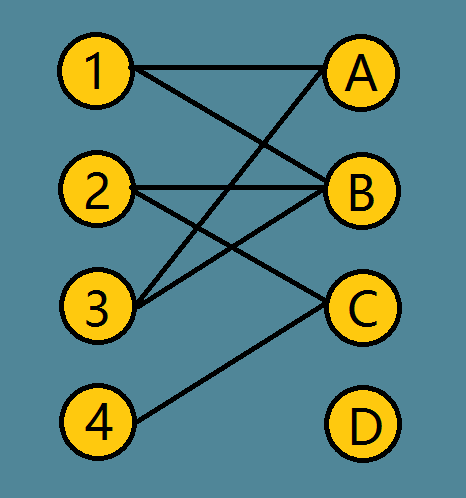
先从1出发，找增广路，找到1->A 这条路，标记并记录。

从2出发，找到2->B这条路，标记并记录。

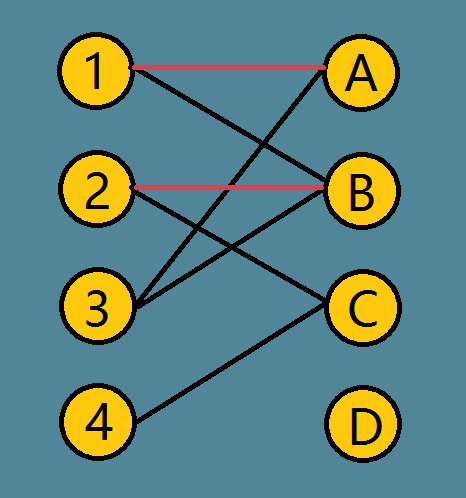
从3开始找，发现3所连接边全部被占用，这时进行一个神奇的操作：

从三开始找一条增广路，3 -> A -> 1 -> B -> 2 -> C 

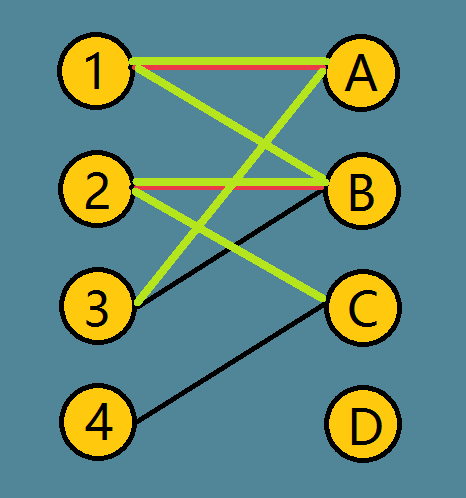
这时，在图中将有两种颜色的边删去，留下绿色的边。

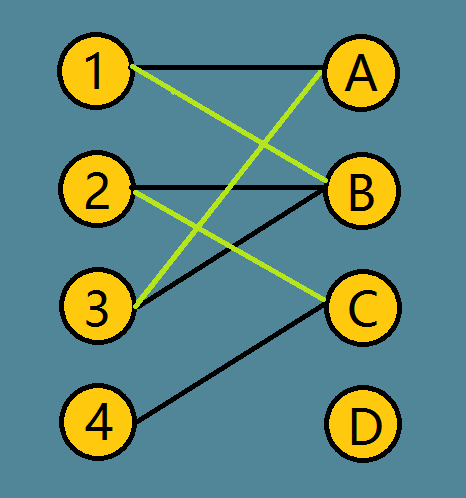
这时，这张图的最大匹配值就是3.

 

三.算法模板

 核心代码：

 1 bool Hungary ( int x ) {
 2          for ( int i = head[ x ] ; i ; i = E[ i ] . next ) {
 3                  if ( vis[ i ] ) continue ;
 4                  int temp = E[ i ] . to ; 
 5                  vis[ i ] = true ;
 6                  if ( !match[ temp ] || Hungary ( match[ temp ] ) ) {
 7                           match [ temp ] = x ;
 8                           return true ;
 9                  }
10          }
11          return false ;
12 }

主程序：

for ( k=1 ; k<=M ; ++k ) {
                 memset ( vis , false , sizeof ( vis ) ) ; 
                 if ( !Hungary ( k ) )
                         break ; 
}

 

时间复杂度：
邻接矩阵： O(n3)
邻接表： O(nm)
 
空间复杂度：
邻接矩阵： O(n2)
邻接表：O(n+m)

2016-09-16 02:18:44

(完)

posted @ 2016-09-16 02:31  SHHHS  阅读(7941)  评论(0)  编辑  收藏  举报