Radix Sort

为了完成二维数据快速分类，最先使用的是hash分类。

前几天我突然想，既然基数排序的时间复杂度也不高，而且可能比hash分类更稳定，所以不妨试一下。

在实现上我依次实现：

1、一维数组基数排序

基本解决主要问题，涵盖排序，包含改进的存储分配策略。

如果用链表来实现，大量的函数调用将耗费太多时间。

2、二维数组基数排序

主要是实现和原有程序的集成。

 

一、数据结构

下面是存储节点的主数据结构。

typedef struct tagPageList{
    int * PagePtr;
    struct tagPageList * next;
}PageList;

typedef struct tagBucket{
    int * currentPagePtr;
    int offset;
    PageList pl;
    PageList * currentPageListItem;
}Bucket;

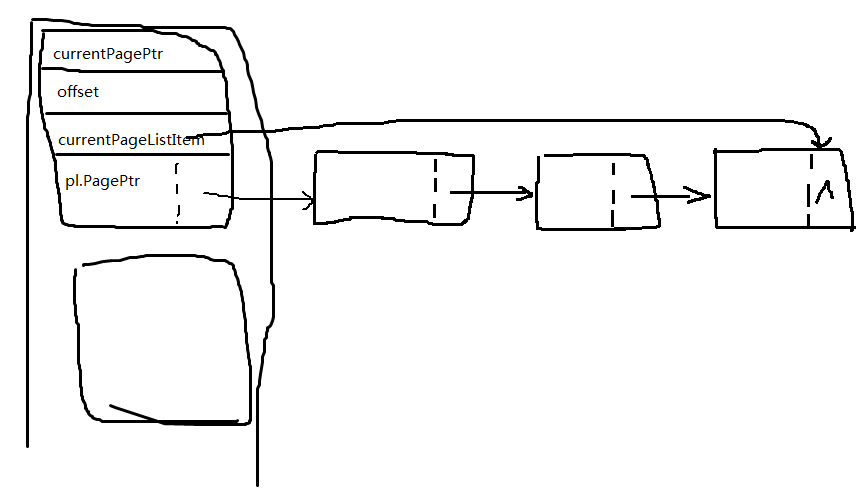
链表内是存储的一个4KB页面的指针。

每4KB页面可以存储最多1024个记录序号，如果是一维数组排序，那就直接存储数组元素了。

 

二、算法

基数排序可以分为MSD或者LSD。这里用的是LSD。

伪代码如下：

for i=0 to sizeof(sorted-element-type){
    for each sorted-num{
        cell = sorted-num
        bucketIdx = (cell>>8*i)&0xff
        bucket[bucketIdx] = cell
    }
    combine linked list nodes to overwrite original array
}

 

 

C代码实现：

int main(){
    HANDLE heap = NULL;
    Bucket bucket[BUCKETSLOTCOUNT];
    PageList * pageListPool;
    int plpAvailable = 0;
    int * pages = NULL;
    int * pagesAvailable = NULL;
    int * objIdx;
    unsigned short * s;

    time_t timeBegin;
    time_t timeEnd;

    heap = HeapCreate(HEAP_NO_SERIALIZE|HEAP_GENERATE_EXCEPTIONS, 1024*1024, 0);
    if (heap != NULL){
        pages = (int * )HeapAlloc(heap, 0, (TFSI/PAGEGRANULAR + BUCKETSLOTCOUNT + 8) * 4096);
        pageListPool = (PageList *)HeapAlloc(heap, 0, (TFSI/PAGEGRANULAR + 8) * sizeof(PageList));
        s = (unsigned short *)HeapAlloc(heap, 0, TFSI*sizeof(unsigned short));
        objIdx = (int *)HeapAlloc(heap, 0, TFSI * sizeof(int));
    }
    MakeSure(pages != NULL && pageListPool != NULL && objIdx != NULL);

    for(int i=0; i<TFSI; i++) objIdx[i]=i;
    timeBegin = clock();
    for (int i=0; i<TFSI; i++) s[i] = rand();
    timeEnd = clock();
    printf("\n%f(s) consumed in generating numbers", (double)(timeEnd-timeBegin)/CLOCKS_PER_SEC);
    
    timeBegin = clock();

    for (int t=0; t<sizeof(short); t++){
        FillMemory(pages, (TFSI/PAGEGRANULAR + BUCKETSLOTCOUNT + 8) * 4096, 0xff);
        SecureZeroMemory(pageListPool, (TFSI/PAGEGRANULAR + 8) * sizeof(PageList));
        pagesAvailable = pages;
        plpAvailable = 0;

        for(int i=0; i<256; i++){
            bucket[i].currentPagePtr = pagesAvailable;
            bucket[i].offset = 0;
            bucket[i].pl.PagePtr = pagesAvailable;
            bucket[i].pl.next = NULL;
            pagesAvailable += PAGEGRANULAR;
            bucket[i].currentPageListItem = &(bucket[i].pl);
        }

        int bucketIdx;
        for (int i=0; i<TFSI; i++){
            bucketIdx = (s[objIdx[i]]>>t*8)&0xff;
            MakeSure(bucketIdx < 256);
            //save(bucketIdx, objIdx[i]);
            bucket[bucketIdx].currentPagePtr[ bucket[bucketIdx].offset ] = objIdx[i];
            bucket[bucketIdx].offset++;
            if (bucket[bucketIdx].offset == PAGEGRANULAR){
                bucket[bucketIdx].currentPageListItem->next = &pageListPool[plpAvailable];
                plpAvailable++;
                MakeSure(plpAvailable < TFSI/PAGEGRANULAR + 8);
                bucket[bucketIdx].currentPageListItem->next->PagePtr = pagesAvailable;
                bucket[bucketIdx].currentPageListItem->next->next = NULL;
                
                bucket[bucketIdx].currentPagePtr = pagesAvailable;
                bucket[bucketIdx].offset = 0;
                pagesAvailable += PAGEGRANULAR;
                MakeSure(pagesAvailable < pages+(TFSI/PAGEGRANULAR + BUCKETSLOTCOUNT + 8) * 1024);
            
                bucket[bucketIdx].currentPageListItem = bucket[bucketIdx].currentPageListItem->next;
            }
        }

        //update objIdx index
        int start = 0;
        for (int i=0; i<256; i++){
            PageList * p;
            p = &(bucket[i].pl);
            while (p){
                for (int t=0; t<PAGEGRANULAR; t++){
                    int idx = p->PagePtr[t];
                    if (idx != TERMINATOR){
                        objIdx[start] = idx;
                        start++;
                    }
                    if (idx == TERMINATOR) break;
                }
                p = p->next;
            }
        }
    }

    timeEnd = clock();
    printf("\n%f(s) consumed in generating results", (double)(timeEnd-timeBegin)/CLOCKS_PER_SEC);

    //for (int i=0; i<TFSI; i++) printf("%d\n", s[objIdx[i]]);

    HeapFree(heap, 0, pages);
    HeapFree(heap, 0, pageListPool);
    HeapFree(heap, 0, s);
    HeapFree(heap, 0, objIdx);
    HeapDestroy(heap);

    return 0;
}

 

三、测试结果。

i7 3632QM @2.2GHz ==>TB 3.2GHz/ 8G RAM/  win8 64bit/VS2012 win32 release 

1024*1024*100，1亿个随机生成 short 型数据。
1.438000(s) consumed in generating random numbers
4.563000(s) consumed in radix sort 
12.719000(s) consumed in qsort
7.641000(s) consumed in std::sort

 

1024*1024*5   500万随机生成 short 型数据。
0.078000(s) consumed in generating random numbers
0.172000(s) consumed in radix sort 
0.656000(s) consumed in qsort
0.390000(s) consumed in std::sort

 

1024*500
0.000000(s) consumed in generating random numbers
0.015000(s) consumed in radix sort 
0.063000(s) consumed in qsort
0.047000(s) consumed in std::sort

 

四、讨论

二维数据分类上，性能相当于hash分类 约 1/3 。

比库例程稍快，慢的主要原因还是存储器，如果只是解决一维数组的话，调整下可以更快。

但对于二维数组多个线程同时操作，排序是不可接受的。