NOIP2001提高组
第一题 一元三次方程求解
【题目描述】
有形如:ax^3+bx^2+cx+d=0 这样的一个一元三次方程。给出该方程中各项的系数(a,b,c,d 均为实数),并约定该方程存在三个不同实根(根的范围在-100至100之间),且根与根之差的绝对值>=1。要求由小到大依次在同一行输出这三个实根(根与根之间留有空格),并精确到小数点后2位。
【输入格式】
仅一行,a,b,c,d四个实数
【输出格式】
仅一行,三个实数根
【样例输出】
1 -5 -4 20
【样例输入】
-2.00 2.00 5.00
【分析】
枚举。
第二题 数的划分
【题目描述】
将整数n分成k份,且每份不能为空,任意两份不能相同(不考虑顺序)。
例如:n=7,k=3,下面三种分法被认为是相同的。
1,1,5; 1,5,1; 5,1,1;
问有多少种不同的分法。
【输入格式】
n,k (6<n<=200,2<=k<=6)
【输出格式】
一个整数,即不同的分法。
【样例输入】
7 3
【样例输出】
4
【分析】
f[i][j]代表将i分为j分的分法。考虑两种情况:
- 至少一个1。f[i – 1][j - 1]
- 没有1。f[i – j][j]
第三题 统计单词个数
【题目描述】
给出一个长度不超过200的由小写英文字母组成的字母串(约定:该字串以每行20个字母的方式输入,且保证每行一定为20个)。要求将此字母串分成k份(1<k≤40),且每份中包含的单词个数加起来总数最大(每份中包含的单词可以部分重叠。当选用一个单词之后,其第一个字母不能再用。例如字符串this中可以包含this和is,选用this之后就不能包含t)。在给出的一个不超过6个单词的字典中,要求输出最大的单词个数。
【输入格式】
第一行有二个正整数:(p,k),其中p表示字串的行数;k表示分为k个部分。
接下来的p行,每行均有20个字符。
再接下来有一个正整数s,表示字典中单词个数。(l≤s≤6)
接下来的s行,每行均有一个单词。
【输出格式】
结果输出至屏幕,每行一个整数,分别对应每组测试数据的相应结果。
【样例输入】
1 3
thisisabookyouareaoh
4
is
a
ok
sab
【样例输出】
7
【分析】
动态规划。f[i][j]表示到第i个字母,分为j分得到的最多单词数。
f[i][j] = max(f[k][j – 1] + s[k + 1][i])。s[i][j]代表从i到j的单词个数。
第四题 car的旅行路线
【题目描述】
又到暑假了,住在城市A的Car想和朋友一起去城市B旅游。她知道每个城市都有四个飞机场,分别位于一个矩形的四个顶点上,同一个城市中两个机场之间有一条笔直的高速铁路,第I个城市中高速铁路了的单位里程价格为Ti,任意两个不同城市的机场之间均有航线,所有航线单位里程的价格均为t。
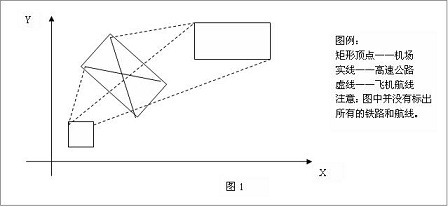
注意:图中并没有
标出所有的铁路与航线。
那么Car应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题,于是她来向你请教。
找出一条从城市A到B的旅游路线,出发和到达城市中的机场可以任意选取,要求总的花费最少。
【输入格式】
第一行为一个正整数n(0<=n<=10),表示有n组测试数据。
每组的第一行有四个正整数s,t,A,B。
S(0<S<=100)表示城市的个数,t表示飞机单位里程的价格,A,B分别为城市A,B的序号,(1<=A,B<=S)。
接下来有S行,其中第I行均有7个正整数xi1,yi1,xi2,yi2,xi3,yi3,Ti,这当中的(xi1,yi1),(xi2,yi2),(xi3,yi3)分别是第I个城市中任意三个机场的坐标,T I为第I个城市高速铁路单位里程的价格。
【输出格式】
共有n行,每行一个数据对应测试数据
要求保留一位小数
【样例输入】
1
3 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3
【样例输出】
47.5
【分析】
构建图,然后最短路。因为起点和终点各有四个点。可以构建出两个点,分别只和起点的四个点和终点的四个点相连。路的长度赋值为0。没有路的点之间长度初始化为极大值。
代码
第一题
#include<cstring>
#include<cstdio>
using namespace std;
double ans[4];
double a,b,c,d;
double f(double xt)
{
double s;
s=xt*xt*xt+b*xt*xt+c*xt+d;
return s;
}
int main()
{
scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
b/=a; c/=a; d/=a;
double x1,x2; int p=0;
for (int x=-10000;x<=10000;x++)
{
x1=(x-0.05)/100.0; x2=(x+0.05)/100.0;
if (f(x/100.0)==0 || f(x1)*f(x2)<0)
{
p++; ans[p]=x/100.0;
}
if (p==3) break;
}
for (int i=1;i<=2;i++)
for (int j=2;j<=3;j++)
if (ans[i]>ans[j])
{
double t=ans[i];ans[i]=ans[j];ans[j]=t;
}
for (int i=1;i<=p-1;i++)
printf("%.2lf ",ans[i]);
printf("%0.2lf\n",ans[p]);
return 0;
}
第二题
#include <stdio.h>
#define maxn 300
int f[maxn][maxn];
int n,m;
int main()
{
scanf("%d%d",&n,&m);
f[0][0]=1;
for (int i=1;i<=n;++i)
for (int j=1;j<=m;++j)
if (i-j>=0)
f[i][j]=f[i-j][j]+f[i-1][j-1];
printf("%d\n",f[n][m]);
return 0;
}
第三题
#include <stdio.h>
#include <string.h>
#define MAXN 300
char s[MAXN],te[30];
int f[MAXN][MAXN],from[MAXN][MAXN];
int len,p,k,S;
struct ss {
int len;
char s[MAXN];
} word[10];
int main() {
scanf("%d%d",&p,&k);
for (int i = 0;i < p;++i) {
scanf("%s",te);
for (int j = 0;j < 20;++j)
s[++len] = te[j];
}
scanf("%d",&S);
for (int i = 1;i <= S;++i) {
scanf("%s",word[i].s);
word[i].len = strlen(word[i].s);
}
int i,fe,j,l,h,g;
for (i = 1;i <= len;++i) {
for (fe = 1;fe <= k && fe <= i;++fe)
for (j = fe - 1;j < i;++j) {
int tot = 0;
for (l = j + 1;l <= i;++l)
for (h = 1;h <= S;++h)
if (l + word[h].len - 1 <= i) {
bool same = 1;
for (g = 1;g <= word[h].len;++g)
if (s[l + g - 1] != word[h].s[g - 1]) {
same = 0;
break;
}
if (same) {
++tot;
break;
}
}
if (f[j][fe - 1] + tot > f[i][fe]) {
from[i][fe] = j;
f[i][fe] = f[j][fe - 1] + tot;
}
}
int tte = 0;
++tte;
}
printf("%d\n",f[len][k]);
return 0;
}
第四题
#include <math.h>
#include <stdio.h>
#include <string.h>
#define MAXN 110
#define MAXINT 10000010
struct ss {
int x,y;
} node[MAXN];
bool v[MAXN];
double dis[MAXN][MAXN],tdis[MAXN];
int x[4],y[4];
int s,t,a,b,tot,te,str,end;
int cheng(int x1,int y1,int x2,int y2,int x3,int y3) {
int ex = x1 - x2,ey = y1 - y2,dx = x3 - x2,dy = y3 - y2;
return ex * dx + ey * dy;
}
double Dis(int x1,int y1,int x2,int y2) {
return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}
void dij(int str,int end) {
for (int i = 1;i <= tot;++i)
tdis[i] = dis[str][i];
v[str] = 1;
while (1) {
double min = MAXINT;
int k = 0;
for (int i = 1;i <= tot;++i)
if ((!v[i]) && (tdis[i] < min)) {
k = i;
min = tdis[i];
}
if (!k)
break;
v[k] = 1;
for (int i = 1;i <= tot;++i)
if ((!v[i]) && (tdis[k] + dis[k][i] < tdis[i]))
tdis[i] = tdis[k] + dis[k][i];
}
printf("%.1lf\n",tdis[end]);
}
int init() {
memset(node,0,sizeof(node));
memset(v,0,sizeof(v));
memset(dis,0,sizeof(dis));
scanf("%d%d%d%d",&s,&t,&a,&b);
str = 4 * s + 1;
end = 4 * s + 2;
tot = 0;
for (int i = 1;i <= end;++i)
for (int j = 1;j <= end;++j)
dis[i][j] = MAXINT;
for (int i = 1;i <= s;++i) {
scanf("%d%d%d%d%d%d%d",&x[1],&y[1],&x[2],&y[2],&x[3],&y[3],&te);
if (!cheng(x[1],y[1],x[2],y[2],x[3],y[3])) {
x[0] = x[3] - x[2] + x[1];
y[0] = y[3] - y[2] + y[1];
} else {
if (!cheng(x[2],y[2],x[1],y[1],x[3],y[3])) {
x[0] = x[3] - x[1] + x[2];
y[0] = y[3] - y[1] + y[2];
} else {
if (!cheng(x[1],y[1],x[3],y[3],x[2],y[2])) {
x[0] = x[2] - x[3] + x[1];
y[0] = y[2] - y[3] + y[1];
}
}
}
int st = tot + 1;
for (int j = 0;j < 4;++j) {
node[++tot].x = x[j];
node[tot].y = y[j];
}
for (int j = st;j <= tot;++j)
for (int k = st;k <= tot;++k)
dis[j][k] = Dis(node[j].x,node[j].y,node[k].x,node[k].y) * te;
if (i == a)
for (int j = st;j <= tot;++j)
dis[str][j] = 0;
if (i == b)
for (int j = st;j <= tot;++j)
dis[j][end] = 0;
}
for (int i = 1;i <= tot;++i)
for (int j = 1;j <= tot;++j)
if (dis[i][j] == MAXINT)
dis[i][j] = Dis(node[i].x,node[i].y,node[j].x,node[j].y) * t;
tot += 2;
dij(str,end);
}
int main() {
int tt;
scanf("%d",&tt);
for (int i = 1;i <= tt;++i)
init();
return 0;
}

