【11/4】模拟赛
第一题 神奇的风
【题目描述】
T博士最近在研究一种神奇的风。
这种风有一个源头,称之为“风口”。风口的风要么是顺时针的,要么是逆时针的。
这种风是有能量的。
这种风是能传播的,如果风口周围都能传播风,风会像这样产生下一级的风:
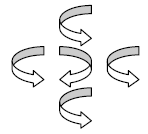
(箭头表示风的转向,最中间的是风口,图中风口的风是顺时针的,对于风口的风是逆时针的情形可通过物理模型想象一下或由这个图推理。)
产生的下一级风的能量依据新产生的风所在的地形决定,有两种可以传递这种风的地形:
一、平地,下一级风的能量与风口的风能量相等..,这种地形用“.”表示。
二、少量障碍物,下一级风的能量是风口的风能量的一半,这种地形用“*”表示。
每个新产生的风都能作为新的风口继续产生下一级风。
此外,还有一种地形是不能传递风的:大量障碍物,用“#”表示。
如果在风口的某一方向是“#”地形,则该方向不会产生下一级风,其他方向视该位置的地形而定,就是说,如果是“.”或“*”地形则该方向照样传播。
T博士还发现了这种神奇的风的叠加规则:两股风叠加时,无论它们的转向是否相同,都只保留能量较大的那股风,即风叠加后的能量和转向都与叠加前能量较大的那股风相同。而如果叠加的两股风的能量相同且转向相同,则保留其中任意一股。两股风能量相同且转向不同时叠加的情况未知,因为T博士至今还没碰到这样的情况。
T博士画了几张地图,他想知道地图上的某点风的转向和能量。
【输入格式】
输入文件wind.in的第一行是两个整数m和n,表示地图大小为m行n列。
接下来的m行,每行是n个字符,只会是以下的几种:
“S”表示风口,保证图中有且仅有一个“S”。
“E”表示目的地,即T博士想知道的那个点。
“.”“*”“#”见描述。
第m+2行是一个整数“0”或“1”,分别表示风口的风是顺时针方向或逆时针方向。
约定“S”处的风能量为16384,“S”和“E”处的地形均为平地。
【输出格式】
输出文件为wind.out。
若目的地会有风传到,则输出两行:第一行为一个整数,为目的地的风的能量;第二行为一个整数“0”或“1”,表示意义同输入格式。此种情形下保证目的地的风的能量大于0。
若目的地没有风传到,则输出一行:“There’s no wind!”(双引号内的字符,全英文标点)。
【样例输入】
| 样例输入1 | 样例输入2 | 样例输入3 |
|
3 4 |
2 4 |
6 8 |
【样例输出】
| 样例输出1 | 样例输出2 | 样例输出3 |
| 4096 1 |
16384 1 |
There’s no wind! |
【数据范围】
对于20%的数据,m,n均不超过10。
对于50%的数据,m,n均不超过100。
对于100%的数据,m,n均不超过200。
【分析】
根据题目描述进行模拟。
第二题 消息传播
【题目描述】
众所周知,HYF有很多小姊妹。
HYF每天放学之后都要跟(不同的)MM约会。HYF这天约会的时候不巧被jzt撞上了……虽然换一个新的MM约会这种事情对于HYF来说如同家常便饭,所谓“好事不出门,坏事传千里”,jzt迅速将这个消息传播开来。
每个听到这个消息的人首先会震惊一段时间(他怎么又换MM了- -~!),但是这样的震惊只会持续2个时刻(因为这对于HYF来说太正常了= =~!)。如果他在第i个时刻听到这个消息,就会从第(i+2)个时刻开始传播这个消息,每个时刻把这个消息告诉两个人,当然他只会告诉不知道这个消息的人。但是当他连续告诉了10个人之后,他就会口干舌燥,停止传播。
jzt在第0时刻撞到HYF(当然jzt也有震惊时间),请问第N时刻共有多少人知道了这个消息?
【输入格式】
一行一个整数N,表示第N时刻。
【输出格式】
一行一个整数,表示N分钟后知道这个消息的总人数。
【样例输入】
| 样例输入1 | 样例输入2 | 样例输入3 |
| 4 | 1 | 10 |
【样例输出】
| 样例输出1 | 样例输出2 | 样例输出3 |
| 11 | 1 | 651 |
【数据范围】
20%的数据,N<=20
60%的数据,N<=1000
100%的数据,N<=10000
【分析】
每个人存在7中状态。我们发现,状态之间是有递推关系的。
设h数组。h[1]~h[5]代表现在正在传播的人,h[6]是还剩1刻传播的人。每过一个时刻,整个数组都是右移一位,新的指导的人就是h[1]~h[5]的总和乘以2。
但是如果我们每次都去移动数组,很费时间。思考上面式子。将其化为递推式f[n] = f[n – 1] + (f[n – 2] + f[n – 7]) * 2。
然后加入高精度。
第三题 窈窕淑女
【题目描述】
“关关雎鸠,在河之洲。窈窕淑女,君子好逑。”——《诗经》
T博士的大儿子阿T(阿嚏?)最近遇到了一件麻烦事。
有n个MM同时邀请阿T在8月14日上午11:30拜访她们家,可那时阿T刚比赛完,所以不能先提前拜访几个,而他又不会分身术,所以他只得分别拜访。他共有T分钟的时间可以用于拜访MM。他还安排好了拜访的顺序,对于每个MM都可以选择拜访或不拜访。对于要.拜访的MM必须按阿T安排好的顺序拜访。
对于每个MM都有如下数据:
不高兴系数x,为2到9的整数。
不高兴度X,若阿T迟到t分钟到她家,则X=x^t(x的t次方);若阿T不拜访她家,则X=x^T。
拜访时间y(分钟),保证0<yi<=T,即阿T在她家停留的时间,若阿..T.在到了她家但.停留时间不足y分钟,她的不高兴度就会变成正无穷大。
假设阿T从一个地方到另一个地方不用消耗时间,阿T希望在有限的T分钟里使所有MM的不高兴度之和最小。请告诉他这个最小值是多少。
【输入格式】
输入文件girls.in的第一行是两个正整数n和T。
第1+i(1<=i<=n)有两个正整数xi和yi,分别是阿T安排的拜访顺序中第i个MM的不高兴系数和拜访时间。
【输出格式】
输出文件是girls.out。请只输出一行,仅一个正整数,为最小的不高兴度之和。
【样例输入】
| 样例输入1 | 样例输入2 |
| 2 100 5 30 2 70 |
2 30 5 16 2 16 |
【样例输出】
| 样例输出1 | 样例输出2 |
| 1073741825 | 1073741825 |
【数据范围】
对于20%的数据,满足1<=n<=10,1<=T<=9;
对于50%的数据,满足1<=n<=20,1<=T<=30;
对于100%的数据,满足1<=n<=20,1<=T<=180;
【分析】
刚开始想到了枚举然后处理。因为2^20次方才100多万。但是忘记考虑计算时N的循环。超时必然。
观摩了一下红牛的程序。
f[i][j]代表前i个人,用了j的时间,所达到的最小值。
正推f[i + 1][j] = max(f[i + 1][j],f[i][j] + x[i + 1] ^ t) 不取i + 1这个人。
f[i + 1][j + y[i + 1]] = max(f[i + 1][j + y[i + 1]],f[i][j] + x[i + 1] ^ j)。取走i这个人。
结果在所有的f[n][i]中取最小。
第四题 新版方格取数
【题目描述】
T博士的小儿子小T最近在玩一个游戏。
在一个m行n列的方格中有m*n个数,游戏规则如下:
先在方格边缘取走一个数,以此格为起点,下一步可向该格四个方向中未取数的方格前进,取走该方格的数并继续按如上规则取数。
如果某次取数恰好取到方格的边缘,则下一步可选择离开方格另取入口进入方格,当然也可以选择按上述规则取数。
游戏在小T取完方格内所有数或无法继续取方格内剩下的任何一个数的时候结束。
游戏有这样的得分规则:若方格内的某数j是方格内所有数中第i个取走的数,此次取数的得分为i*j。
小T最后的得分为游戏结束时他各次取数的得分之和。
小T想知道他所能取得的最大得分。
注意:已经取走数的方格不能再次取数或经过。
【输入格式】
输入文件newfgqs.in的第一行是两个正整数m和n,表示方格为m行n列。
第2到m+1行,每行为n个非负整数(注意可能为0),是方格里的数,保证这些数都小于100000(10万)。
【输出格式】
输出文件为newfgqs.out。
只要输出一行,为小T能取得的最大得分。
【样例输入】
| 样例输入1 | 样例输入2 |
|
3 3 |
3 3 |
【样例输出】
| 样例输出1 | 样例输出2 |
| 285 | 9 |
【数据范围】
对于50%的数据,满足m*n<=9。
对于100%的数据,满足m*n<=16。
【分析】
不会。
代码
第一题
#include <stdio.h>
#define MAXN 210
int xx[4] = {1,-1,0,0};
int yy[4] = {0,0,1,-1};
struct ss {
int x,y;
} q[500010];
char a[MAXN][MAXN];
int e[MAXN][MAXN],d[MAXN][MAXN];
bool v[MAXN][MAXN];
int n,m,sx,sy,ex,ey;
bool inmap(int x,int y) {
return (x > 0) && (x <= n) && (y > 0) && (y <= m);
}
void find(int x,int y) {
int l,r,tx,ty,tex,tey;
l = r = 0;
q[0].x = x;
q[0].y = y;
v[x][y] = 1;
while (l <= r) {
tx = q[l].x;
ty = q[l].y;
for (int i = 0;i < 4;++i) {
tex = tx + xx[i];
tey = ty + yy[i];
if ((!inmap(tex,tey)) || (a[tex][tey] == '#'))
continue;
if (a[tex][tey] == '.') {
if (e[tx][ty] > e[tex][tey]) {
e[tex][tey] = e[tx][ty];
if (!d[tx][ty])
d[tex][tey] = 1;
else
d[tex][tey] = 0;
if (!v[tex][tey]) {
q[++r].x = tex;
q[r].y = tey;
v[tex][tey] = 1;
}
}
} else {
if (a[tex][tey] == '*') {
if (e[tx][ty] / 2 > e[tex][tey]) {
e[tex][tey] = e[tx][ty] / 2;
if (!d[tx][ty])
d[tex][tey] = 1;
else
d[tex][tey] = 0;
if (!v[tex][tey]) {
q[++r].x = tex;
q[r].y = tey;
v[tex][tey] = 1;
}
}
}
}
}
++l;
v[tx][ty] = 0;
}
}
int main() {
freopen("wind.in","r",stdin);
freopen("wind.out","w",stdout);
scanf("%d%d",&n,&m);
scanf("%c",&a[1][1]);
for (int i = 1;i <= n;++i) {
for (int j = 1;j <= m;++j) {
scanf("%c",&a[i][j]);
if (a[i][j] == 'S') {
sx = i;
sy = j;
a[i][j] = '.';
}
if (a[i][j] == 'E') {
ex = i;
ey = j;
a[i][j] = '.';
}
if (a[i][j] == '#')
v[i][j] = 1;
}
scanf("%c",&a[0][0]);
}
a[0][0] = 0;
for (int i = 0;i <= n + 1;++i) {
v[i][0] = 1;
v[i][m + 1] = 1;
}
for (int i = 0;i <= m + 1;++i) {
v[0][i] = 1;
v[n + 1][i] = 1;
}
scanf("%d",&d[sx][sy]);
e[sx][sy] = 16384;
find(sx,sy);
if (!e[ex][ey])
printf("There's no wind!\n");
else
printf("%d\n%d\n",e[ex][ey],d[ex][ey]);
return 0;
}
第二题
#include <stdio.h>
#include <string.h>
#include <iostream>
#define MAXN 10010
#define MAXL 1001
using namespace std;
int n,f[MAXN][MAXL],tem[MAXL],te[MAXL];
void jia(int a[],int b[],int c[]) {
memset(c,0,sizeof(c));
int x,len;
len = max(a[0],b[0]);
x = 0;
for (int i = 1;i <= len;++i) {
x = a[i] + b[i] + x;
c[i] = x % 1000000;
x /= 1000000;
}
if (x)
c[++len] = x;
c[0] = len;
}
void jian(int a[],int b[],int c[]) {
int len = a[0],x = 0,d[MAXL];
memset(c,0,sizeof(c));
memset(d,0,sizeof(d));
for (int i = 0;i < MAXL;++i)
d[i] = a[i];
for (int i = 1;i <= len;++i) {
if (d[i] < b[i]) {
--d[i + 1];
d[i] += 1000000;
}
c[i] = d[i] - b[i];
}
while (!c[len])
--len;
c[0] = len;
}
int main() {
freopen("spread.in","r",stdin);
freopen("spread.out","w",stdout);
scanf("%d",&n);
for (int i = 0;i < 7;++i)
f[i][0] = 1;
f[0][1] = f[1][1] = 1;
f[2][1] = 3;
f[3][1] = 5;
f[4][1] = 11;
f[5][1] = 21;
f[6][1] = 43;
for (int i = 7;i <= n;++i) {
jian(f[i - 2],f[i - 7],tem);
jia(tem,tem,te);
jia(f[i - 1],te,f[i]);
}
printf("%d",f[n][f[n][0]]);
for (int i = f[n][0] - 1;i > 0;--i)
printf("%d%d%d%d%d%d",f[n][i] / 100000,f[n][i] / 10000 % 10,f[n][i] / 1000 % 10,f[n][i] / 100 % 10,f[n][i] / 10 % 10,f[n][i] % 10);
return 0;
}
第三题
#include <stdio.h>
#include <string.h>
#include <iostream>
#define MAXN 21
#define MAXT 190
#define BASE 10000
using namespace std;
struct ss {
int g[100];
} f[MAXN][MAXT],mi[10][MAXT],ans;
int n,t;
int x[MAXN],y[MAXN];
ss small(ss a,ss b) {
if (a.g[0] == -1)
return b;
if (b.g[0] == -1)
return a;
if (a.g[0] < b.g[0])
return a;
if (a.g[0] > b.g[0])
return b;
for (int i = a.g[0];i > 0;--i) {
if (a.g[i] < b.g[i])
return a;
if (a.g[i] > b.g[i])
return b;
}
return a;
}
ss jia(ss a,ss b) {
ss c;
memset(c.g,0,sizeof(c.g));
c.g[0] = max(a.g[0],b.g[0]);
int x = 0;
for (int i = 1;i <= c.g[0];++i) {
c.g[i] = x + a.g[i] + b.g[i];
x = c.g[i] / BASE;
c.g[i] %= BASE;
}
if (x)
c.g[++c.g[0]] = x;
return c;
}
ss cheng(ss a,int b) {
ss c;
memset(c.g,0,sizeof(c.g));
c.g[0] = a.g[0];
int x = 0;
for (int i = 1;i <= a.g[0];++i) {
c.g[i] = a.g[i] * b;
c.g[i] += x;
x = c.g[i] / BASE;
c.g[i] %= BASE;
}
if (x)
c.g[++c.g[0]] = x;
return c;
}
void out(ss a) {
printf("%d",a.g[a.g[0]]);
for (int i = a.g[0] - 1;i > 0;--i)
printf("%d%d%d%d",a.g[i] / 1000,a.g[i] / 100 % 10,a.g[i] / 10 % 10,a.g[i] % 10);
}
int main() {
freopen("girls.in","r",stdin);
freopen("girls.out","w",stdout);
scanf("%d%d",&n,&t);
for (int i = 1;i <= n;++i)
scanf("%d%d",&x[i],&y[i]);
for (int i = 2;i <= 9;++i)
mi[i][0].g[0] = mi[i][0].g[1] = 1;
for (int i = 2;i <= 9;++i)
for (int j = 1;j <= t;++j)
mi[i][j] = cheng(mi[i][j - 1],i);
for (int i = 0;i <= n;++i)
for (int j = 0;j <= t;++j)
f[i][j].g[0] = -1;
f[0][0].g[0] = 1;
int tr = 0;
for (int i = 0;i < n;++i)
for (int j = 0;j <= t;++j)
if (f[i][j].g[0] != -1) {
f[i + 1][j] = small(f[i + 1][j],jia(f[i][j],mi[x[i + 1]][t]));
if (j + y[i + 1] <= t)
f[i + 1][j + y[i + 1]] = small(f[i + 1][j + y[i + 1]],jia(f[i][j],mi[x[i + 1]][j]));
++tr;
}
ans.g[0] = -1;
for (int i = 0;i <= t;++i)
if (f[n][i].g[0] != -1)
ans = small(ans,f[n][i]);
out(ans);
return 0;
}
第四题
#include <stdio.h>
#define MAXN 20
const int xx[4] = {0,0,1,-1};
const int yy[4] = {1,-1,0,0};
int n,m;
int a[MAXN][MAXN];
bool v[MAXN][MAXN];
long long ans;
bool inmap(int x,int y) {
return (x > 0) && (x <= n) && (y > 0) && (y <= m);
}
bool inwall(int x,int y) {
return (x == 1) || (x == n) || (y == 1) || (y == m);
}
void findin(int x,int y,long long teans,int num);
void findout(long long teans,long long num) {
for (int i = 1;i <= m;++i)
if (!v[1][i])
findin(1,i,teans,num);
for (int i = 2;i <= n;++i) {
if (!v[i][1])
findin(i,1,teans,num);
if (!v[i][m])
findin(i,m,teans,num);
}
for (int i = 2;i < m;++i)
if (!v[n][i])
findin(n,i,teans,num);
}
void findin(int x,int y,long long teans,int num) {
v[x][y] = 1;
teans += a[x][y] * num;
if (teans > ans)
ans = teans;
int tex,tey;
for (int i = 0;i < 4;++i) {
tex = x + xx[i];
tey = y + yy[i];
if ((!inmap(tex,tey)) || (v[tex][tey]))
continue;
findin(tex,tey,teans,num + 1);
}
if (inwall(x,y))
findout(teans,num + 1);
v[x][y] = 0;
}
int main() {
freopen("newfgqs.in","r",stdin);
freopen("newfgqs.out","w",stdout);
scanf("%d%d",&n,&m);
for (int i = 1;i <= n;++i)
for (int j = 1;j <= m;++j)
scanf("%d",&a[i][j]);
findout(0,1);
printf("%d\n",ans);
return 0;
}

