[easy高精度]Hanoi双塔问题

【题目描述】

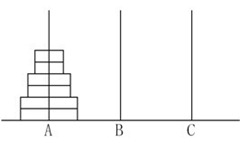
给定A、B、C三根足够长的细柱，在A柱上放有2n个中间有孔的圆盘，共有n个不同的尺寸，每个尺寸都有两个相同的圆盘，注意这两个圆盘是不加区分的（下图为n=3的情形）。现要将这些圆盘移到C柱上，在移动过程中可放在B柱上暂存。要求：
（1）每次只能移动一个圆盘；
（2）A、B、C三根细柱上的圆盘都要保持上小下大的顺序；
任务：设An为2n个圆盘完成上述任务所需的最少移动次数，对于输入的n，输出An。

【输入格式】

一个正整数n，表示在A柱上放有2n个圆盘。

【输出格式】

仅一行，包含一个正整数, 为完成上述任务所需的最少移动次数An。

【样例输入】

样例输入1	样例输入2
1	2

【样例输出】

样例输出1	样例输出2
2	6

【分析】

设f[n]为有2 * n个圆盘，所需移动的步数。

分三步：

1. 将2 * n - 2个盘子移动到B，所用的步数是f[n – 1]
2. 将最后的两个移动到C上，所用步数是2
3. 将2 * n - 2个盘子移动到C，所用的步数是f[n – 1]

那么f[n] = 2 * f[n – 1] + 2;

f[n] + 2 = 2 * (f[n – 1] + 2);

f[n] = 2 ^ (n + 1) – 2;

然后就是高精度了。

#include <stdio.h>
#include <string.h>
#define MAXLEN 110
#define BASE 10000
int ans[MAXLEN],b[MAXLEN];
int n;
void cheng1(int a[]) {
  int c[MAXLEN];
  memset(c,0,sizeof(c));
  for (int i = 1;i <= a[0];++i)
    for (int j = 1;j <= a[0];++j) {
      int x = i + j - 1;
      c[x] += a[i] * a[j];
      c[x + 1] += c[x] / BASE;
      c[x] %= BASE;
    }
  c[0] = a[0] * 2;
  for (int i = 1;i <= c[0];++i) {
    c[i + 1] += c[i] / BASE;
    c[i] %= BASE;
  }
  while (c[c[0] + 1])
    ++c[0];
  while ((!c[c[0]]) && (c[0] > 1))
    --c[0];
  for (int i = 0;i < MAXLEN;++i)
    a[i] = c[i];
}
void cheng2(int a[]) {
  int c[MAXLEN];
  memset(c,0,sizeof(c));
  for (int i = 1;i <= a[0];++i)
    c[i] = a[i] * 2;
  c[0] = a[0] + 1;
  for (int i = 1;i <= c[0];++i) {
    c[i + 1] += c[i] / BASE;
    c[i] %= BASE;
  }
  while (c[c[0] + 1])
    ++c[0];
  while ((!c[c[0]]) && (c[0] > 1))
    --c[0];
  for (int i = 0;i < MAXLEN;++i)
    a[i] = c[i];
}
void pow2(int x) {
  if (x == 1)
    return;
  pow2(x / 2);
  cheng1(ans);
  if (x & 1)
    cheng2(ans);
}
int main() {
  scanf("%d",&n);
  ans[0] = 1;
  ans[1] = 2;
  ++n;
  pow2(n);
  if (ans[1] >= 2)
    ans[1] -= 2;
  else {
    int now = 1;
    while (!ans[now + 1])
      ++now;
    for (int i = now;i > 0;--i) {
      --ans[i + 1];
      ans[i] += BASE;
    }
    ans[1] -= 2;
  }
  printf("%d",ans[ans[0]]);
  for (int i = ans[0] - 1;i > 0;--i)
    printf("%d%d%d%d",ans[i] / 1000,
                      ans[i] / 100 % 10,
                      ans[i] / 10 % 10,
                      ans[i] % 10);
  return 0;
}