[O(N)的我不会]树网的核

【题目描述】

设T=(V, E, W) 是一个无圈且连通的无向图（也称为无根树），每条边带有正整数的权，我们称T为树网（treenetwork），其中V, E分别表示结点与边的集合，W表示各边长度的集合，并设T有n个结点。

路径：树网中任何两结点a,b都存在唯一的一条简单路径，用d(a,b)表示以a,b为端点的路径的长度，它是该路径上各边长度之和。我们称d(a,b)为a,b两结点间的距离。

一点v到一条路径P的距离为该点与P上的最近的结点的距离：

d(v，P)=min{d(v，u)，u为路径P上的结点}。

树网的直径：树网中最长的路径称为树网的直径。对于给定的树网T，直径不一定是唯一的，但可以证明：各直径的中点（不一定恰好是某个结点，可能在某条边的内部）是唯一的，我们称该点为树网的中心。

偏心距ECC(F)：树网T中距路径F最远的结点到路径F的距离，即 ECC(F)=max{d(v,F),v∈V}.

任务：对于给定的树网T=(V, E,W)和非负整数s，求一个路径F，它是某直径上的一段路径（该路径两端均为树网中的结点），其长度不超过s（可以等于s），使偏心距ECC(F)最小。我们称这个路径为树网T=(V,E,W)的核（Core）。必要时，F可以退化为某个结点。一般来说，在上述定义下，核不一定只有一个，但最小偏心距是唯一的。

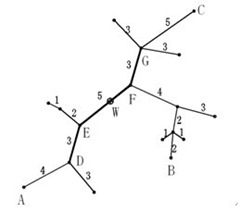
下面的图给出了树网的一个实例。图中，A-B与A-C是两条直径，长度均为20。点W是树网的中心，EF边的长度为5。如果指定s=11，则树网的核为路径DEFG（也可以取为路径DEF），偏心距为8。如果指定s=0（或s=1、s=2），则树网的核为结点F，偏心距为12。

【输入格式】

输入文件包含n行：
第1行，两个正整数n和s，中间用一个空格隔开。其中n为树网结点的个数，s为树网的核的长度的上界。设结点编号依次为1, 2, ..., n。
从第2行到第n行，每行给出3个用空格隔开的正整数，依次表示每一条边的两个端点编号和长度。例如，“2 4 7”表示连接结点2与4的边的长度为7。
所给的数据都是正确的，不必检验。

【输出格式】

输出文件只有一个非负整数，为指定意义下的最小偏心距。

【样例输入】

5 2
1 2 5
2 3 2
2 4 4
2 5 3

【样例输出】

5
【分析】

首先找到一个树的直径。方法是：从1点出发，找到距离1最远的点，记为x。然后从x出发，所搜索到的最远路径就是树的直径。

然后我们用搜索的方法计算每个点到直径的最短距离dist。

之后在直径上枚举路径的起点和终点。找到最小的偏心距。

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

#include <stdio.h>
#include <string.h>
#include <limits.h>
#define MAXN 310
struct tnode {
  int num;
  tnode *next;
} g[MAXN],*t;
int q[MAXN * 3],list[MAXN],loc[MAXN],dist[MAXN],from[MAXN],dis[MAXN],
    di[MAXN][MAXN],xdis[MAXN][MAXN];
int n,l,r,s,x,y,z,tot,ans;
bool v[MAXN],in_tree[MAXN];
void insert(int x,tnode &p) {
  t = new(tnode);
  t->num = x;
  t->next = p.next;
  p.next = t;
}
void dfs(int father,int x) {
  tnode *tt;
  tt = g[x].next;
  while (tt != NULL) {
    int y = tt->num;
    if (!in_tree[y])
      if (dist[x] + di[x][y] < dist[y]) {
        dist[y] = dist[x] + di[x][y];
        from[y] = father;
        dfs(father,y);
      }
    tt = tt->next;
  }
}
int main() { 
  scanf("%d%d",&n,&s);
  for (int i = 1;i < n;++i) {
    scanf("%d%d%d",&x,&y,&z);
    insert(x,g[y]);
    insert(y,g[x]);
    di[x][y] = z;
    di[y][x] = z;
  }
  q[0] = 1;
  v[1] = 1;
  while (l <= r) {
    x = q[l];
    t = g[x].next;
    while (t != NULL) {
      y = t->num;
      if (y != from[x])
      if (dis[y] < di[x][y] + dis[x]) {
        dis[y] = di[x][y] + dis[x];
        from[y] = x;
        if (!v[y]) {
          q[++r] = y;
          v[y] = 1;
        }
      }
      t = t->next;
    }
    ++l;
    v[x] = 0;
  }
  z = 0;
  for (int i = 1;i <= n;++i)
    if (dis[i] > z) {
      z = dis[i];
      x = i;
    }
  memset(from,0,sizeof(from));
  memset(v,0,sizeof(v));
  v[x] = 1;
  memset(dis,0,sizeof(dis));
  q[0] = x;
  v[x] = 1;
  l = r = 0;
  while (l <= r) {
    x = q[l];
    t = g[x].next;
    while (t != NULL) {
      y = t->num;
      if (from[x] != y)
      if (dis[y] < di[x][y] + dis[x]) {
        dis[y] = di[x][y] + dis[x];
        from[y] = x;
        if (!v[y]) {
          q[++r] = y;
          v[y] = 1;
        }
      }
      t = t->next;
    }
    ++l;
    v[x] = 0;
  }
  z = 0;
  for (int i = 1;i <= n;++i)
    if (dis[i] > z) {
      z = dis[i];
      x = i;
    }
  list[++tot] = x;
  while (from[x]) {
    x = from[x];
    list[++tot] = x;
  }
  for (int i = 1;i <= tot;++i) {
    loc[list[i]] = i;
    in_tree[list[i]] = 1;
  }
  for (int i = 1;i <= tot;++i)
    for (int j = i + 1;j <= tot;++j)
      xdis[i][j] = xdis[i][j - 1] + di[list[j - 1]][list[j]];
  memset(from,0,sizeof(from));
  for (int i = 1;i <= n;++i)
    if (!in_tree[i])
      dist[i] = INT_MAX;
  for (int i = 1;i <= tot;++i)
    dfs(list[i],list[i]);
  ans = INT_MAX;
  for (int st = 1;st <= tot;++st)
    for (int en = st;en <= tot;++en) {
      if (xdis[st][en] > s)
        break;
      int te_ans = 0;
      for (int i = 1;i <= n;++i)
        if (!in_tree[i]) {
          if (dist[i] > te_ans)
            te_ans = dist[i];
        } else {
          x = loc[i];
          if (x < st) {
            if (dist[i] + xdis[x][st] > te_ans)
              te_ans = dist[i] + xdis[x][st];
          }
          if (x > en) {
            if (dist[i] + xdis[en][x] > te_ans)
              te_ans = dist[i] + xdis[en][x];
          }
        }
      if (te_ans < ans)
        ans = te_ans;
    }
  printf("%d\n",ans);
  return 0;
}