Logistic回归分类算法原理分析与代码实现
前言
本文将介绍机器学习分类算法中的Logistic回归分类算法并给出伪代码,Python代码实现。
(说明:从本文开始,将接触到最优化算法相关的学习。旨在将这些最优化的算法用于训练出一个非线性的函数,以用于分类。)
算法原理
首先要提到的概念是回归。
对于回归这个概念,在以后的文章会有系统而深入的学习。简单的说,回归就是用一条线对N多数据点进行一个拟合,这个拟合的过程就叫做回归。
Logistic回归分类算法就是对数据集建立回归公式,以此进行分类。
而至于如何寻找最佳回归系数,或者说是分类器的训练,就需要使用到最优化算法了。
回归分类器的形式
基本形式是用每个特征都乘以一个回归系数,然后把所有的结果值相加。
这样算出的很多结果都是连续的,不利于分类,故可以将结果再带入到一个Sigmoid函数以得到一些比较离散的分类结果。
Sigmoid函数的轮廓如下:

这样,计算的结果会是一个0-1的值。进而0.5以上归为一类,以下归为一类即可。(一般的逻辑回归只能解决两个分类的问题)
接下来的工作重点就转移到了最佳回归系数的确定了。
最佳回归系数的确定
确定最佳回归系数的过程,也就是对数据集进行训练的过程。
求最佳回归系数的步骤如下:
1. 列出分类函数:
(θ 指回归系数,在实践中往往会再对结果进行一个Sigmoid转换)
2. 给出分类函数对应的错误估计函数:

(m为样本个数)
只有当某个θ向量使上面的错误估计函数J(θ)取得最小值的时候,这个θ向量才是最佳回归系数向量。
3. 采用梯度下降法或者最小二乘法求错误函数取得最小值的时候θ的取值:

为表述方便,上式仅为一个样本的情况,实际中要综合多个样本的情况需要进行一个求和 (除非你使用后面会介绍的随机梯度上升算法),具体请参考下面的代码实现部分。
将步骤 2 中的错误函数加上负号,就可以把问题转换为求极大值,梯度下降法转换为梯度上升法。
更详尽的推导部分,在以后专门分析回归的文章中给出。
基于梯度上升法的最佳回归参数拟合
梯度上升法求最大值的核心思想是将自变量沿着目标函数的梯度方向移动,一直移动到指定的次数或者说某个允许的误差范围。
基于梯度上升法的分类伪代码:
1 每个回归系数初始化为1 2 重复R次: 3 计算整个数据集的梯度 4 使用 alpha * gradient 更新回归系数向量 5 返回回归系数
下面给出完整的实现及测试代码(用到的数据集文件共 4 列,前 3 列为特征,最后一列为分类结果):
1 #!/usr/bin/env python 2 # -*- coding:UTF-8 -*- 3 4 ''' 5 Created on 2014-12-29 6 7 @author: fangmeng 8 ''' 9 10 import numpy 11 12 #===================================== 13 # 输入: 14 # 空 15 # 输出: 16 # dataMat: 测试数据集 17 # labelMat: 测试分类标签集 18 #===================================== 19 def loadDataSet(): 20 '创建测试数据集,分类标签集并返回。' 21 22 # 测试数据集 23 dataMat = []; 24 # 测试分类标签集 25 labelMat = [] 26 # 文本数据源 27 fr = open('/home/fangmeng/testSet.txt') 28 29 # 载入数据 30 for line in fr.readlines(): 31 lineArr = line.strip().split() 32 dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) 33 labelMat.append(int(lineArr[2])) 34 35 return dataMat,labelMat 36 37 38 #===================================== 39 # 输入: 40 # inX: 目标转换向量 41 # 输出: 42 # 1.0/(1+numpy.exp(-inX)): 转换结果 43 #===================================== 44 def sigmoid(inX): 45 'sigmoid转换函数' 46 47 return 1.0/(1+numpy.exp(-inX)) 48 49 #===================================== 50 # 输入: 51 # dataMatIn: 数据集 52 # classLabels: 分类标签集 53 # 输出: 54 # weights: 最佳拟合参数向量 55 #===================================== 56 def gradAscent(dataMatIn, classLabels): 57 '基于梯度上升法的logistic回归分类器' 58 59 # 将数据集,分类标签集存入矩阵类型。 60 dataMatrix = numpy.mat(dataMatIn) 61 labelMat = numpy.mat(classLabels).transpose() 62 63 # 上升步长度 64 alpha = 0.001 65 # 迭代次数 66 maxCycles = 500 67 # 初始化回归参数向量 68 m,n = numpy.shape(dataMatrix) 69 weights = numpy.ones((n,1)) 70 71 # 对回归系数进行maxCycles次梯度上升 72 for k in range(maxCycles): 73 h = sigmoid(dataMatrix*weights) 74 error = (labelMat - h) 75 weights = weights + alpha * dataMatrix.transpose()* error 76 77 return weights 78 79 def test(): 80 '测试' 81 82 dataArr, labelMat = loadDataSet() 83 print gradAscent(dataArr, labelMat) 84 85 if __name__ == '__main__': 86 test()
测试结果:

拟合结果展示
可使用matplotlib画决策边界,用作分析拟合结果是否达到预期。
绘制及测试部分代码如下所示:
1 #====================================== 2 # 输入: 3 # weights: 回归系数向量 4 # 输出: 5 # 图形化的决策边界演示 6 #====================================== 7 def plotBestFit(weights): 8 '决策边界演示' 9 10 import matplotlib.pyplot as plt 11 # 获取数据集 分类标签集 12 dataMat,labelMat=loadDataSet() 13 dataArr = numpy.array(dataMat) 14 15 # 两种分类下的两种特征列表 16 xcord1 = []; ycord1 = [] 17 xcord2 = []; ycord2 = [] 18 for i in range(numpy.shape(dataArr)[0]): 19 if int(labelMat[i])== 1: 20 xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) 21 else: 22 xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) 23 24 fig = plt.figure() 25 ax = fig.add_subplot(111) 26 ax.scatter(xcord1, ycord1, s=30, c='red', marker='s') 27 ax.scatter(xcord2, ycord2, s=30, c='green') 28 29 # 绘制决策边界 30 x = numpy.arange(-3.0, 3.0, 0.1) 31 y = (-weights[0]-weights[1]*x)/weights[2] 32 ax.plot(x, y) 33 34 plt.xlabel('X1'); plt.ylabel('X2'); 35 plt.show() 36 37 def test(): 38 '测试' 39 40 dataArr, labelMat = loadDataSet() 41 weights = gradAscent(dataArr, labelMat) 42 plotBestFit(weights.getA())
测试结果:

更好的求最值方法 - 随机梯度上升
Logistic回归的本质其实就是求拟合参数,而求拟合参数最核心的就是求错误估计函数的最小值。
仔细分析上面的代码,会发现该分类的效率做多的耗费也是在求最值上面。由于每次都要用所有数据来计算梯度,导致数据集非常大的时候,该算法很不给力。
实践表明,每次仅仅用一个样本点来更新回归系数,当所有样本算完,也能达到相似的效果(仅仅是相似,或者说接近)。
由于可以在每个样本到达的时候对分类器进行增量式更新,因此随机梯度上升算法其实是一个在线学习算法。
基于随机梯度上升的分类伪代码:
1 所有回归系数初始化为1 2 对数据集中的每个样本: 3 计算该样本的梯度 4 使用 alpha * gradient 更新回归系数值 5 返回回归系数值
请对比上面的基本梯度上升算法进行理解学习。
优化之后的分类算法函数如下:
1 #===================================== 2 # 输入: 3 # dataMatIn: 数据集(注意是向量类型) 4 # classLabels: 分类标签集 5 # 输出: 6 # weights: 最佳拟合参数向量 7 #===================================== 8 def stocGradAscent0(dataMatrix, classLabels): 9 '基于随机梯度上升法的logistic回归分类器' 10 11 m,n = numpy.shape(dataMatrix) 12 # 上升步长度 13 alpha = 0.01 14 # 初始化回归参数向量 15 weights = numpy.ones(n) 16 17 # 对回归系数进行样本数量次数的梯度上升,每次上升仅用一个样本。 18 for i in range(m): 19 h = sigmoid(sum(dataMatrix[i]*weights)) 20 error = classLabels[i] - h 21 weights = weights + alpha * error * dataMatrix[i] 22 return weights
你也许会疑惑 "不是说随机梯度上升算法吗?随机呢?",不用急,很快就会提到这个。
分析优化后的代码可以看到两个区别:一个是当前分类结果变量h和误差变量都是数值类型(之前为向量类型),二是无矩阵转换过程,数据集为numpy向量的数组类型。
测试结果:

对比优化前的算法结果,可以看出分类错误率更高了。
优化后的效果反而更差了?这样说有点不公平,因为优化后的算法只是迭代了100次,而优化前的足足有500次。
那么接下来可以进一步优化,理论依据为:增加迭代计算的次数,当达到一个接近收敛或者已经收敛的状态时,停止迭代。
那么如何做到这点呢?
第一是要动态的选定步长,第二,就是每次随机的选定样本,这就是为什么叫做随机梯度上升算法了。
最终修改后的分类器如下:
1 #===================================== 2 # 输入: 3 # dataMatIn: 数据集(注意是向量类型) 4 # classLabels: 分类标签集 5 # 输出: 6 # weights: 最佳拟合参数向量 7 #===================================== 8 def stocGradAscent1(dataMatrix, classLabels, numIter=150): 9 '基于随机梯度上升法的logistic回归分类器' 10 11 m,n = numpy.shape(dataMatrix) 12 weights = numpy.ones(n) 13 14 # 迭代次数控制 15 for j in range(numIter): 16 # 样本选择集 17 dataIndex = range(m) 18 # 随机选取样本遍历一轮 19 for i in range(m): 20 # 动态修正步长 21 alpha = 4/(1.0+j+i)+0.0001 22 # 随机选取变量进行梯度上升 23 randIndex = int(numpy.random.uniform(0,len(dataIndex))) 24 h = sigmoid(sum(dataMatrix[randIndex]*weights)) 25 error = classLabels[randIndex] - h 26 weights = weights + alpha * error * dataMatrix[randIndex] 27 # 从选择集中删除已经使用过的样本 28 del(dataIndex[randIndex]) 29 return weights
运行结果:
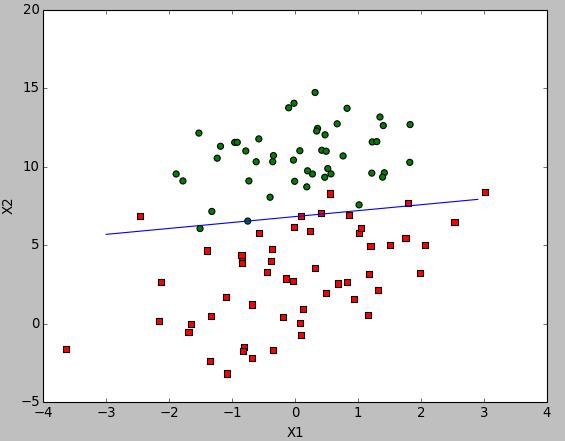
这次,和最原始的基于梯度上升法分类器的结果就差不多了。但是迭代次数大大的减少了。
网上也有一些非常严格的证明随机梯度上升算法的收敛速度更快(相比基础梯度上升算法)的证明,有兴趣的读者可以查找相关论文。
小结
1. 逻辑回归的计算代价不高,是很常用的分类算法。集中基于随机梯度上升的逻辑回归分类器能够支持在线学习。
2. 但逻辑回归算法缺点很明显 - 一般只能解决两个类的分类问题。
3. 另外逻辑回归容易欠拟合,导致分类的精度不高。


