朴素贝叶斯分类算法原理分析与代码实现
前言
本文介绍机器学习分类算法中的朴素贝叶斯分类算法并给出伪代码,Python代码实现。
词向量
朴素贝叶斯分类算法常常用于文档的分类,而且实践证明效果是挺不错的。
在说明原理之前,先介绍一个叫词向量的概念。 --- 它一般是一个布尔类型的集合,该集合中每个元素都表示其对应的单词是否在文档中出现。
对应关系和词汇表一一对应。
比如说,词汇表只有三个单词:'apple', 'orange', 'melo',某文档中,apple和melo出现过,那么其对应的词向量就是 {1, 0, 1}。
这种模型通常称为词集模型,如果词向量元素是整数类型,每个元素表示相应单词在文档中出现的次数(0表示不出现),那这种模型就叫做词袋模型。
如下部分代码可用于由文档构建词向量以及测试结果:
1 #==================================== 2 # 输入: 3 # 空 4 # 输出: 5 # postingList: 文档列表 6 # classVec: 分类标签列表 7 #==================================== 8 def loadDataSet(): 9 '创建测试数据' 10 11 # 这组数据是从斑点狗论坛获取的 12 postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'], 13 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'], 14 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'], 15 ['stop', 'posting', 'stupid', 'worthless', 'garbage'], 16 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'], 17 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']] 18 19 # 1 表示带敏感词汇 20 classVec = [0,1,0,1,0,1] 21 22 return postingList,classVec 23 24 #==================================== 25 # 输入: 26 # dataSet: 文档列表 27 # 输出: 28 # list(vocabSet): 词汇表 29 #==================================== 30 def createVocabList(dataSet): 31 '创建词汇表' 32 33 vocabSet = set([]) 34 for document in dataSet: # 遍历文档列表 35 # 首先将当前文档的单词唯一化,然后以交集的方式加入到保存词汇的集合中。 36 vocabSet = vocabSet | set(document) 37 38 return list(vocabSet) 39 40 #==================================== 41 # 输入: 42 # vocabList: 词汇表 43 # inputSet: 待转换文档 44 # 输出: 45 # returnVec: 转换结果 - 词向量 46 #==================================== 47 def setOfWords2Vec(vocabList, inputSet): 48 '将文档转换为词向量' 49 50 returnVec = [0]*len(vocabList) 51 for word in inputSet: 52 if word in vocabList: 53 returnVec[vocabList.index(word)] = 1 54 else: print "单词: %s不在词汇表当中" % word 55 return returnVec 56 57 def test(): 58 '测试' 59 60 listOPosts, listClasses = loadDataSet() 61 myVocabList = createVocabList(listOPosts) 62 print setOfWords2Vec(myVocabList, listOPosts[0])
测试结果:

算法原理
不论是用于训练还是分类的文档,首先一致处理为词向量。
通过贝叶斯算法对数据集进行训练,从而统计出所有词向量各种分类的概率。
对于待分类的文档,在转换为词向量之后,从训练集中取得该词向量为各种分类的概率,概率最大的分类就是所求分类结果。
训练算法剖析:如何计算某个词向量的概率
由贝叶斯准则可知,某词向量X为分类 Ci 的概率可用如下公式来进行计算:
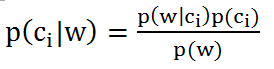
p(ci)表示该文档为分类ci的概率;p(w)为该文档对应词向量为w的概率;这两个量是很好求的,这里不多解释。
关键要解决的是 p(w|ci),也即在文档为分类 ci 的条件下,词向量为w的概率。
这里就要谈到为什么本文讲解的算法名为 "朴素" 贝叶斯。所谓朴素,就是整个形式化过程只做最原始假设。
也就是说,假设不同的特征是相互独立的。但这和现实世界不一致,也导致了其他各种形形色色的贝叶斯算法。
在这样的假设前提下 p(w|ci) = p(w0|ci) * p(w1|ci) * p(w2|ci) * .... * p(wn|ci)
前面提到了w是指词向量,这里wn的含义就是词向量中的某个单词。
可使用如下伪代码计算条件概率 p(wn|ci):
1 对每篇训练文档: 2 对每个类别: 3 增加该单词计数值 4 增加所有单词计数值 5 对每个类别: 6 对每个单词: 7 将该单词的数目除以单词总数得到条件概率 8 返回所有单词在各个类别下的条件概率
请注意如下的具体代码中,对应上述伪代码的第2行,第8行的部分都采用了向量来计算:
1 #============================================= 2 # 输入: 3 # trainMatrix: 文档矩阵 4 # trainCategory: 分类标签集 5 # 输出: 6 # p0Vect: 各单词在分类0的条件下出现的概率 7 # p1Vect: 各单词在分类1的条件下出现的概率 8 # pAbusive: 文档属于分类1的概率 9 #============================================= 10 def trainNB0(trainMatrix,trainCategory): 11 '朴素贝叶斯分类算法' 12 13 # 文档个数 14 numTrainDocs = len(trainMatrix) 15 # 文档词数 16 numWords = len(trainMatrix[0]) 17 # 文档属于分类1的概率 18 pAbusive = sum(trainCategory)/float(numTrainDocs) 19 # 属于分类0的词向量求和 20 p0Num = numpy.zeros(numWords); 21 # 属于分类1的词向量求和 22 p1Num = numpy.zeros(numWords) 23 24 # 分类 0/1 的所有文档内的所有单词数统计 25 p0Denom = .0; p1Denom = .0 26 for i in range(numTrainDocs): # 遍历各文档 27 28 # 若文档属于分类1 29 if trainCategory[i] == 1: 30 # 词向量累加 31 p1Num += trainMatrix[i] 32 # 分类1文档单词数累加 33 p1Denom += sum(trainMatrix[i]) 34 35 # 若文档属于分类0 36 else: 37 # 词向量累加 38 p0Num += trainMatrix[i] 39 # 分类0文档单词数累加 40 p0Denom += sum(trainMatrix[i]) 41 42 p1Vect = p1Num/p1Denom 43 p0Vect = p0Num/p0Denom 44 45 return p0Vect,p1Vect,pAbusive 46 47 def test(): 48 '测试' 49 50 listOPosts, listClasses = loadDataSet() 51 myVocabList = createVocabList(listOPosts) 52 53 # 创建文档矩阵 54 trainMat = [] 55 for postinDoc in listOPosts: 56 trainMat.append(setOfWords2Vec(myVocabList, postinDoc)) 57 58 # 对文档矩阵进行朴素贝叶斯分类并返回各单词在各分类条件下的概率及文档为类别1的概率 59 p0V, p1V, pAb = trainNB0(trainMat, listClasses) 60 61 print p0V
测试结果:

朴素贝叶斯分类算法的完整实现
对于此公式:
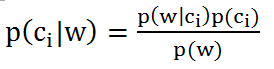
上一步做的工作仅仅是将各个分量求出来了(p(w)为1),而没有进行p(w0|ci) * p(w1|ci) * p(w2|ci) * .... * p(wn|ci)的累乘,也没有进行概率大小的比较。
剩下的工作看似简单但在具体实现上也涉及到两个问题。
问题一:p(wn|ci) 中有一个为0,导致整个累乘结果也为0。这是错误的结论。
解决方法:将所有词的出现次数初始化为1,并将分母初始化为2。
问题二:即使 p(wn|ci) 不为0了,可是它的值也许会很小,这样会导致浮点数值类型的下溢出等精度问题错误。
解决方法:用 p(wn|ci) 的对数进行计算。
具体实现请参考下面代码。针对这两个问题,它对上一步的函数做了一点修改:
特别说明:在下面的代码实现中,w只包含在待分类文档中出现了的单词的特征位。
1 #============================================= 2 # 输入: 3 # trainMatrix: 文档矩阵 4 # trainCategory: 分类标签集 5 # 输出: 6 # p0Vect: 各单词在分类0的条件下出现的概率 7 # p1Vect: 各单词在分类1的条件下出现的概率 8 # pAbusive: 文档属于分类1的概率 9 #============================================= 10 def trainNB0(trainMatrix,trainCategory): 11 '朴素贝叶斯分类算法' 12 13 # 文档个数 14 numTrainDocs = len(trainMatrix) 15 # 文档词数 16 numWords = len(trainMatrix[0]) 17 # 文档属于分类1的概率 18 pAbusive = sum(trainCategory)/float(numTrainDocs) 19 # 属于分类0的词向量求和 20 p0Num = numpy.ones(numWords); 21 # 属于分类1的词向量求和 22 p1Num = numpy.ones(numWords) 23 24 # 分类 0/1 的所有文档内的所有单词数统计 25 p0Denom = 2.0; p1Denom = 2.0 26 for i in range(numTrainDocs): # 遍历各文档 27 28 # 若文档属于分类1 29 if trainCategory[i] == 1: 30 # 词向量累加 31 p1Num += trainMatrix[i] 32 # 分类1文档单词数累加 33 p1Denom += sum(trainMatrix[i]) 34 35 # 若文档属于分类0 36 else: 37 # 词向量累加 38 p0Num += trainMatrix[i] 39 # 分类0文档单词数累加 40 p0Denom += sum(trainMatrix[i]) 41 42 p1Vect = numpy.log(p1Num/p1Denom) 43 p0Vect = numpy.log(p0Num/p0Denom) 44 45 return p0Vect,p1Vect,pAbusive
完善公式的实现,并编写测试代码:
1 #============================================= 2 # 输入: 3 # vec2Classify: 目标对象的词向量的数组形式 4 # p0Vect: 各单词在分类0的条件下出现的概率 5 # p1Vect: 各单词在分类1的条件下出现的概率 6 # pClass1: 文档属于分类1的概率 7 # 输出: 8 # 分类结果 0/1 9 #============================================= 10 def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1): 11 '完成贝叶斯公式剩余部分得到最终分类概率' 12 13 # 为分类1的概率 14 p1 = sum(vec2Classify * p1Vec) + numpy.log(pClass1) 15 # 为分类0的概率 16 p0 = sum(vec2Classify * p0Vec) + numpy.log(1.0 - pClass1) 17 if p1 > p0: 18 return 1 19 else: 20 return 0 21 22 def test(): 23 '测试' 24 25 listOPosts,listClasses = loadDataSet() 26 myVocabList = createVocabList(listOPosts) 27 28 # 创建文档矩阵 29 trainMat=[] 30 for postinDoc in listOPosts: 31 trainMat.append(setOfWords2Vec(myVocabList, postinDoc)) 32 33 # 对文档矩阵进行朴素贝叶斯分类并返回各单词在各分类条件下的概率及文档为类别1的概率 34 p0V,p1V,pAb = trainNB0(numpy.array(trainMat),numpy.array(listClasses)) 35 36 # 测试一 37 testEntry = ['love', 'my', 'dalmation'] 38 thisDoc = numpy.array(setOfWords2Vec(myVocabList, testEntry)) 39 print testEntry,'分类结果: ',classifyNB(thisDoc,p0V,p1V,pAb) 40 41 # 测试二 42 testEntry = ['stupid', 'garbage'] 43 thisDoc = numpy.array(setOfWords2Vec(myVocabList, testEntry)) 44 print testEntry,'分类结果: ',classifyNB(thisDoc,p0V,p1V,pAb)
测试结果:

小结
1. 为突出重点,本文示例仅采用两个分类做测试。更多分类是同理的。
2. 大数据中,程序设计中应尽量以矩阵或者向量为单位来处理数据。这样能简化代码,增加效率,也能提高程序可读性。
3. 该分类算法的优点是对于数据集较少的情况也能适用,能处理多类别问题;然而不足之处在于对数据集的准备方式比较敏感。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号