HectorSLAM论文解析・代码重写（2）

这篇文章为HectorSLAM系列的以下部分

• HectorSLAM的整体逻辑
  • 激光匹配
  • 地图构造
  • 地图更新
• 500行代码重写一个LidarSLAM
  • 测试数据的准备，和测试数据读取模块的编写
  • GUI编写
  • 地图模块的编写
  • 核心模块的编写
    
    • 主循环
    • 匹配算法

参考以下论文

A flexible and scalable SLAM system with full 3D motion estimation
https://www.researchgate.net/publication/228852006_A_flexible_and_scalable_SLAM_system_with_full_3D_motion_estimation

首先绘制一张以扫描匹配为核心的SLAM（例如Hector,Karto_slam,Cartographer..）大概的流程图：

 

基本上以这一类SLAM流程分以下几个部分：

1. motion prediction（运动预测）
2. scan matching（扫描匹配）
3. map update（地图更新）
4. pose update（姿态更新）

 

因为原版的Hector并没有使用车轮odometry。所以运动预测部分仅为根据前一个状态的位置和速度的预测。所以我们直接从跳过motion prediction，下面从２.scan matching（扫描匹配）开始谈起。

１.scan matching（扫描匹配）

所谓匹配就是把从传感器得到的数据和已经知道的地图进行匹配。我们首先假定周围环境是静态的，在静态的环境中，传感器数据应该和已知的地图情报应该高度一致才对。所以在没有噪音的情况下以下方程应该成立：

 

$\sum _{i=0}^{n}\left[ 1-M\left( S_{i}\left( \xi \right) \right) \right] = 0$

 

其中$\xi=\left(p_x,p_y,\psi\right)$代表机器人的姿态(x坐标，y坐标，角度)

Si代表，i号激光束，在姿态ξ下照射到的障碍物的坐标。

M代表某坐标为障碍物的概率。１为100%为障碍物，０为100%空闲区域

在传感器没有噪音，地图已知且没有误差的的情况下，可以求解以上方程，得到未知量ξ（姿态）。直观上来说就是调整姿态使得所有的激光都正确的测量到障碍物。但现实的情况却没有怎么完美，传感器有噪音，地图有误差，且部分未知。所以我们转而求解以下最小二乘：

 

$argmin_{\xi}\sum _{i=0}^{n}\left[ 1-M\left( S_{i}\left( \xi \right) \right) \right]^2$

 

这个式子的求解方法，在论文的公式（９）～（１３）有推导过程。这里虽然不推导（论文已经足够详细），但是仍然建议自己推导一次加深理解。

根据下面的方程我们似乎已经可以通过扫描匹配的方法解出机器人姿态了。

原版的Hector中，为了避免对姿态的求解陷入局部最优解，用了几种不同的分辨率表示地图。首先在分辨率较低的地图中求解姿态，然后逐渐带入较高分辨率的地图中。

 

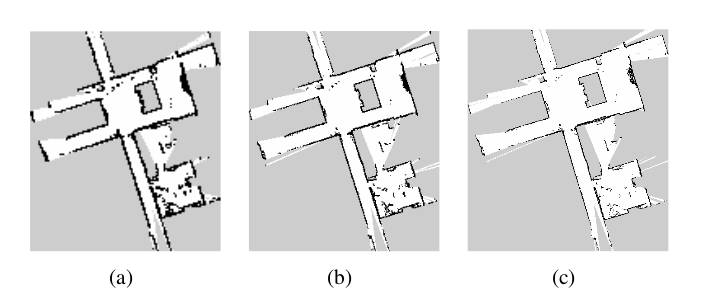
２.地图构造

但为什么只是似乎呢？因为求解以上（12）（13）是需要求M的偏导的，我们知道求解偏导的是需要连续空间的，但Hector使用的格子地图（grid map）存在于离散的空间中。所以，首先我们需要一些方法把我们的离散的格子地图，转换为可以求导的连续地图。论文的 【IV. 2D SLAM】介绍了一种用Bilinear filtering的解决办法：

这个方法直观的理解：比如下图中我们要求点P_m的值时，由于格子地图是离散的，所以并没有办法直接取得。我们转而根据距离P_m最近的4个点P₀₀,P₁₀,P₁₀P₁₁，估计出P_m的取值。

 

越近的点权重越大，具体公式为：

至此我们已经获得了一个可以求偏导的地图，具体的求偏导方法为以下：

 

3.map update（地图更新）

在求解出机器人姿态以后，我们已经能够根据现在姿态更新地图了，

更新地图具体方法为，对于地图的网格的原始数据（raw data）：

• 激光束的顶点（hit），存在障碍物的可能性变高，所以增加一个权重
• 激光束上的其他点（miss），存在障碍物的可能性变小，所以减少一个权重
• 激光束的始点（original point），存在障碍物的可能性变小，所以减少一个权重

根据以下公式可以求出障碍物存在的概率：

$M=\dfrac {e^{x}} {1+e^{x}}$

其中x代表网格的原始数据的值，M代表障碍物存在的概率，这个函数是形如下图：

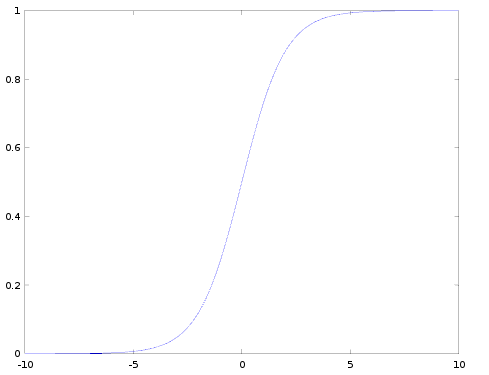
我们可以看网格的原始数据的值越大，越接近1，反之越接近0，很完美的实现的上文中对M的定义

M代表某坐标为障碍物的概率。１为100%为障碍物，０为100%空闲区域

 

 最后更新姿态（并没有需要细说的地方），至此基本的SLAM的框架已经建立好了。

 

既然理论我们已经清楚，那么从下一篇文章开始，我们就用python，手把手把上面的内容用代码实现。