20172305 2018-2019-1 《Java软件结构与数据结构》第八周学习总结
20172305 2018-2019-1 《Java软件结构与数据结构》第八周学习总结
教材学习内容总结
本周内容主要为书第十二章内容:
-
堆(附加属性的二叉树)
- 完全二叉树
- (最小堆)对于每一个结点,它小于或等于其左孩子和右孩子。
- (最大堆)对于每一个结点,它大于或等于其左孩子和右孩子。
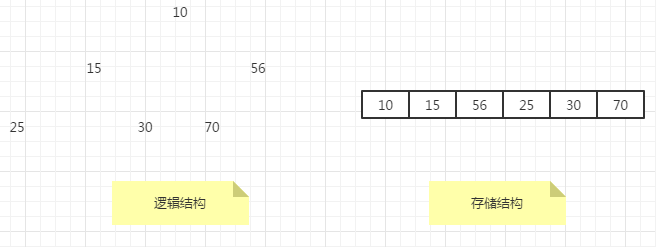
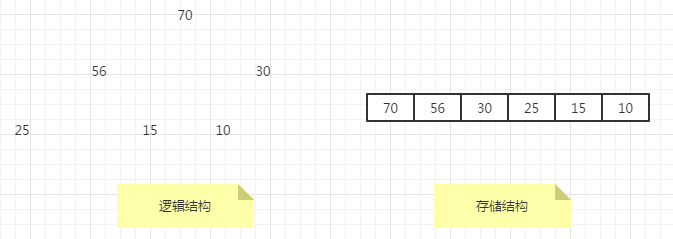
-
最小堆将其最小元素存储在二叉树的根处,其根的两个孩子同样也是最小堆。
-
最大堆将其最大元素存储在二叉树的根处,其根的两个孩子同样也是最大堆。
-
addElement方法将给定的元素添加到堆中的恰当位置处,且维持该堆的完全性属性和有序属性。
- 如果给定元素不是Comparable的,则该方法将会抛出一个ClassCastException异常。
- 对于新插入结点位置要么是第h层左边的下一个空位置,要么是第h+1层左边的第1个位置(h层满的话)。
- 考虑排序属性,将该新值和双亲值进行比较,如果新结点小于双亲则互换位置,沿着树向上继续此过程,直至该新结点要么是大于双亲要么是位于堆的根处。
添加元素0:
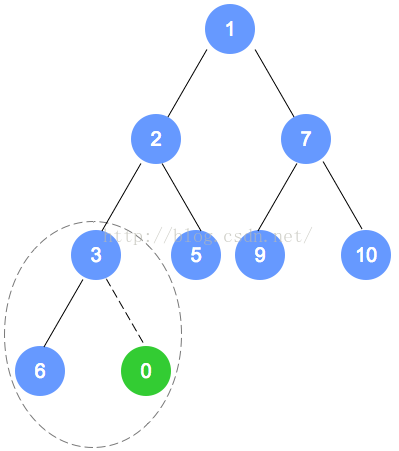
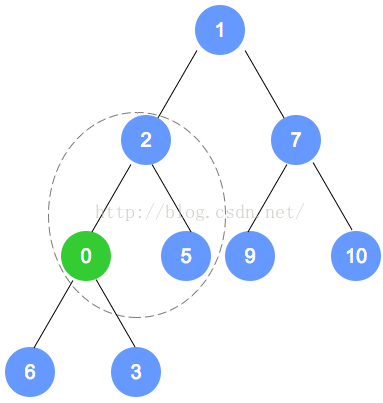
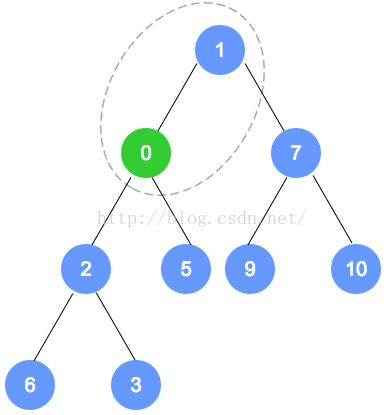
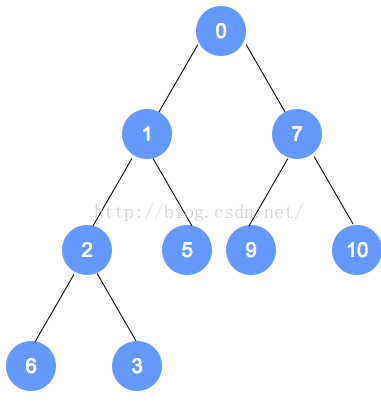
-
removeMin方法将删除最小堆中的最小元素并返回它。
- 由于删除元素是存储在最小堆的根处,所以要返回存储在根处元素并用堆中的最末一片叶子上的元素替代。一旦最末一片叶子的元素移动到根处,则必须要对堆进行重新排序以维持堆的排序属性。
- 新根元素与较小的子结点进行比较,如果子结点更小就替换,沿着树向下这一过程,直至该元素要么位于某片叶子要么比两个子结点都小。
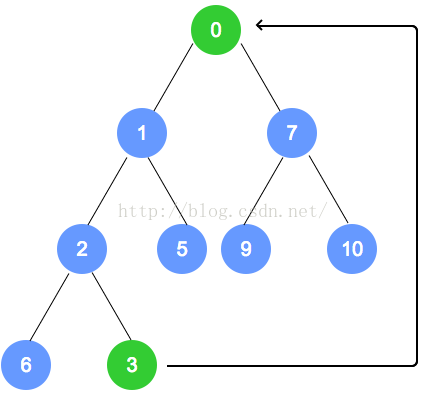
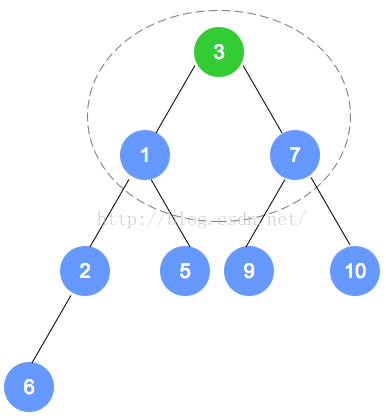
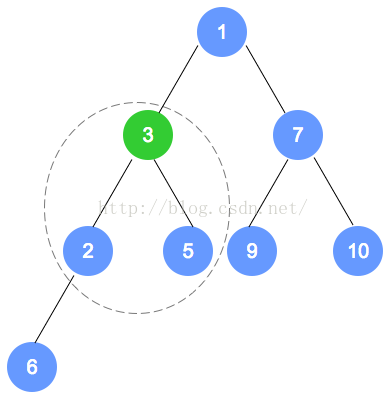
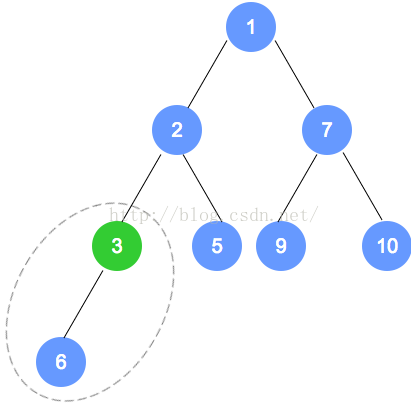
-
findMin方法将返回一个指向最小堆中的最小元素的引用,只需通过返回存储在根处的元素。
-
三种方法的时间复杂度:

-
堆--优先级队列(遵循两个排序规则的集合,具有更高级的项目在先,具有相同优先级的项目使用先进先出的方法来确定其排序)
-
链表实现堆:
- addElement操作使用了两个私有方法getNextParentAdd和heapifyAdd两个方法,getNextParentAdd方法是返回一个指向某结点的引用,该结点为插入结点的双亲。heapifyAdd方法是完成堆的任何重排序,从那片新叶子开始,向上处理至根处。
- 在恰当位置处添加一个新元素,对堆进行重排序来维持排序属性,将lastNode指针重新设定为指定新的最末结点。
- removeMin操作使用了两个私有方法getNewLastNode和heapifyRemove两个方法,getNewLastNode方法返回一个指向某一结点的引用,该结点将是新的最末结点。heapifyRemove方法将完成任何有必要的树重排序,从根向下进行。
- 用存储在最末结点处的元素替换存储在根处的元素,对堆进行重排序,以及返回初始的根元素。
- findMin方法返回一个指向存储在根结点的元素的内容。
-
数组实现堆:
- addElement操作使用了私有方法heapifyAdd方法,用于在必要时对该堆进行重组。
- 在恰当位置处添加新结点,对堆进行重排序来维持排序属性,将count递增。
- removeMin操作使用了私有方法heapifyRemove方法,用于在必要时对该堆进行重组。
- 用存储在最末结点处的元素替换存储在根处的元素,对堆进行重排序,以及返回初始的根元素。
- findMin方法返回一个指向存储在根结点的元素的内容。
-
堆排序

- 将列表的每一个元素添加到堆中,然后在一次一个的将他们从根中删除。
- 最小堆的情况下,排序结果是将该列表以升序排列
- 最大堆的情况下,排序结果是将该列表以降序排列
- 时间复杂度:O(nlogn)
- 空间复杂度:O(1)
教材学习中的问题和解决过程
- 问题1:实现优先级队列的二叉堆、d堆、左式堆、斜堆、二项堆都是什么意思?和最小堆、最大堆有什么区别?
- 问题1解决方案:先说后面的问题,最小堆和最大堆是二叉堆的两种表现形式,最大堆是除了根以外的所有结都要满足:父结点大于子结点;而最小堆恰恰相反,最小堆是除了根以外的所有结都要满足:父结点小于子结点。所以,二叉堆可以根据优先级确定出队列的先后顺序。
- d堆是完全d叉树,就是每一个结点有d个子结点,同时还要满足每个结点从左到右的顺序。
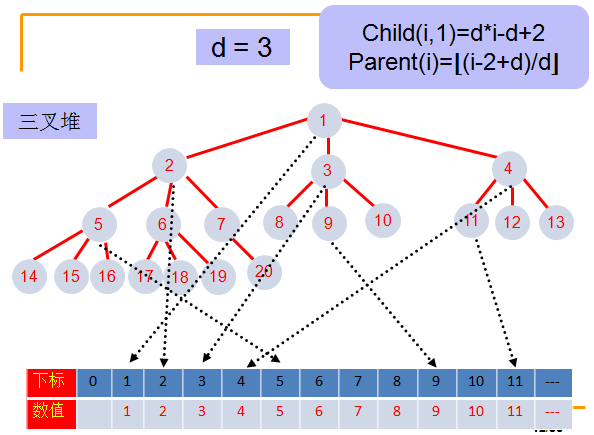
- 左式堆是具有堆序性质的二叉树,左式堆的任意结点的值比其子树的任意结点值均小,但和一般的二叉堆不同,左式堆不再是一棵完全二叉树。

- 斜堆也叫自适应堆,是一种使用二叉树实现的堆状数据结构,使用的是二叉树而不是完全二叉树,所以在整体来看,斜堆会是极不平衡的一个堆,但其合并的速度远远大于二叉堆。

- 二项堆是是二项树的集合或是由一组二项树组成,在O(logn)的时间内即可完成两个二项堆合并操作,所以二项堆是可合并堆,基于二项堆实现的优先队列和进程调度算法有着很好的时间性能。
- d堆是完全d叉树,就是每一个结点有d个子结点,同时还要满足每个结点从左到右的顺序。
代码学习中的问题和解决过程
-
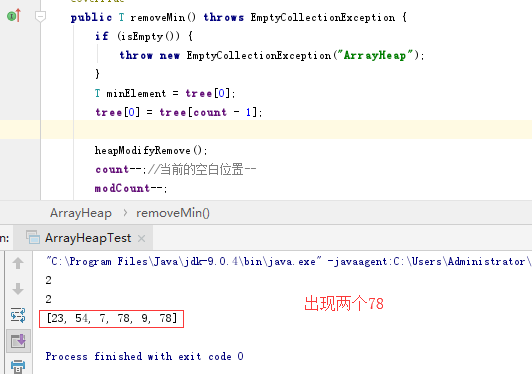
问题1:如何解决数组实现的堆在删除操作之后会输出被删元素?分析数组实现删除添加操作的方法?
-
问题1的解决方案:删除一个元素之后,进行整体的输出会出现被删除元素,通过对代码的分析,在删除最小结点后将末叶结点放到根处之后,没有将叶结点内容进行删除,而是在计数变量和操作次数进行递减,这样的话叶结点和暂时的根结点树都会有同一元素。所以在
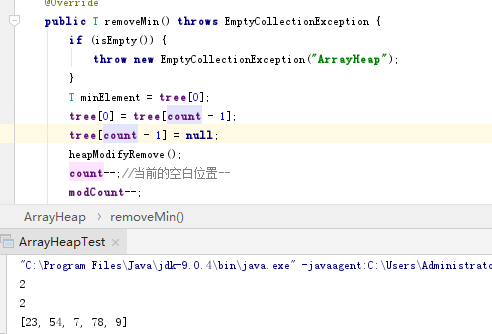
tree[0]=tree[count - 1];和heapifyRemove()之间添加一句tree[count - 1] = null;直接令其为空。针对删除时对堆的排序方法(向下遍历),先判断根结点的左侧和右侧是否为空,如果为空的话就直接跳过循环让新的根结点为根结点,如果不为空的话会有两种情况,只有一个子结点,此时右侧为空,则左侧不为空,记录此时左结点的索引值,如果左右都不为空的话进行判断左侧和右侧谁更小(最小堆)。进入循环,循环条件是索引值小于总共数量和索引值位置与新根结点的比较,node始终是next的父结点的索引值,不断向下遍历,而对于每一个结点他的索引值是n的话,其左子结点为2n+1,右子结点为2(n+1),和之前操作类似,判断来年两个子结点的大小,向下不断遍历,next的值赋给node,并找node的孩子的索引,令next重新指向node的孩子直至不满足next索引值超过总的或是元素大小不符合的时候会跳出循环,node的位置就是替代新结点的位置。针对添加时对堆的排序方法(向上排序),添加的方法进行的排序比较简单,直接确定添加的位置是否比父结点小,如果小的话,进行调换;大得话跳出循环结束排序。和之前的类似,子结点的索引值为count-1的话,那么其父结点位置为next-1/2,不断的和父结点进行比较直至向上遍历结束,当跳出循环后,此时的next位置就是新添结点的位置。未加
tree[count - 1] = null:
添加之后:
-
问题2:PP12.1如何让用堆来实现队列?队列的方法如下:
-
问题2的解决方案:用堆来实现队列的问题,因为队列是一个线性结构,先进先出,而堆是完全二叉树。所以,需要根据把每一个进行队列的元素标上号,按照号码牌的内容来实现堆的形式,但是如果这样的话,我们就不能直接往堆里面插入泛型元素,需要定义个类,而在这个类的内部需要每定义一个就会自增数量,比如先进的是A元素,就为1;再进的是B元素,就为2...以此类推。类似的形式在实验室内就帮助学长实现过,所以定义类个类并不难。但是,需要注意的是要在类中写出比较方法,确定比较元素是谁。但是,我第一次实现的过程中,将这个计数的比较放在外部进行,这样实现的话可以确定谁先进对谁先出队。但是在实现输出队列内容的时候,会发现输出的内容不是进队的形式。而是中序的形式(问题3会解决此问题)。但是,我发现队列的输出形式可以每次删除堆的根结点,用一个暂时变量存放内容,这样的话就复刻了一份堆,利用了复刻的堆实现输出而保持了原堆的内容。但是在实现这种情况会始终出现两个堆被删的一干二净,虽然会按照队列的形式进行输出,但是往后删除就会有问题。经过改写,尝试把删除元素存放到暂时变量中,在给它塞回去。这种方法虽然实现了不报错,但是始终会输出第一个元素,其他元素不输出。我认为是因为我规定的存放数字是第一个就永远第一个。通过侯泽洋同学的交流,发现我的代码都是复制粘贴,没用到继承,如果用继承的话就直接调用父类的方法就可以了,而且规定的标记数字也可以写进方法里面,不用自己规定,保持了队列的完整性。但是,这样的话我还是只输出第一个元素。后来感觉如归的位置重新定义一下,就运行成功了,可能和第一次犯错一样就是在再次入队的时候他的标记数字仍是之前的就会一直输出,重新定义一下就会将之前的标记数字抹去换新。
进行复刻导致两个堆的元素都被删除:
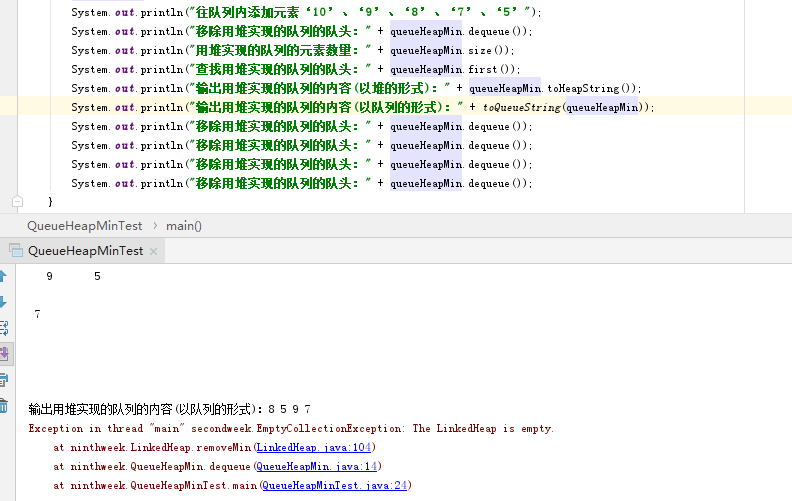
实现队列输出(只是第一个元素的输出):


真正实现队列输出:


-
问题3:如何改写数组实现堆的输出形式?
-
问题3的解决方案:这个问题是在课堂测试上发现的,但是我在ArrayHeap方法里面并没有找到toString方法,但是调用toString没有问题。后来通过单步调试跳到了ArrayBinary的toString。通过继承会调用父类的方法,如过在子类中重写方法会调用子类的方法。链表实现的堆也是如此。所以,针对toString方法我们可以有两种修改方法,一是修改子类重写,二是修改父类直接调用父类的。
代码托管

上周考试错题总结
- 第九章:
- 错题1:Insertion sort is an algorithm that sorts a list of values by repetitively putting a particular value into its final, sorted, position.
- A .true
- B .false
- 错误解析:插入排序是一种反复的把某个元素插入到之前已经排好序的列表中。
- 错题2:The best comparison sort in terms of order is:
- A .O(1)
- B .O(n)
- C .O(log(n))
- D .O(nlog(n))
- 错误解析:根据各个排序方法的比较快速和归并排序都是O(nlogn)的时间复杂度,运行效率高。
- 第十章:
- 错题3:The Java Collections API provides two implementations of balanced binary search trees, TreeSet and TreeMap, both of which use a ___________tree implementation.
- A .AVL
- B .red/black
- C .binary search
- D .None of the above
- 错误解析:通过实验二的第六部分学习,知道两个类都是红黑树。
- 第十一章:
- 错题4:A minheap stores its largest element at the root of the binary tree, and both children of the root of a minheap are also minheaps.
- A .True
- B .Flase
- 错误解析:最小堆将其最小元素存放到根处,不是最大元素,最大堆将其最大元素存放到根处。
- 错题5:Since a heap is a binary search tree, there is only one correct location for the insertion of a new node, and that is either the next open position from the left at level h or the first position on the left at level h+1 if level h is full.
- A .True
- B .Flase
- 错误解析:堆是一个完全树,不是二叉查找树。
-
三章的错题每次测试都差一点点满分,而且在写此部分的过程中发现每道题都是学过的边边角角之类的问题。暴漏出学习的不足,看书还是不够仔细,针对边界类的问题没有仔细思考。
结对与互评
点评(王禹涵)
- 博客中值得学习的或问题:
- 教材总结写的很好,排版整齐。盗图还被称为
丑图有点不太合适吧。问题2的排版可以再调整一下会更好的。
- 教材总结写的很好,排版整齐。盗图还被称为
- 代码中值得学习的或问题:
- 迭代器的问题可以推荐看看第七章的内容,迭代器的输出方式有两种方法可以都去尝试一下!
- 基于评分标准,我给本博客打分:7分。
- 得分情况如下:
- 正确使用Markdown语法(加1分)
- 模板中的要素齐全(加1分)
- 教材学习中的问题和解决过程, 二个问题加2分
- 代码调试中的问题和解决过程, 一个问题加1分
- 感想,体会不假大空的加1分
- 点评认真,能指出博客和代码中的问题的加1分
点评(方艺雯)
- 博客中值得学习的或问题:
- 图片排版不错,问题二的解决方案的文字部分可以稍稍修饰一下,堆排序的部分写的很好很细致,配图也很精细的把每一次结果都放上去了。建议可以更细致化的提出问题。
- 代码中值得学习的或问题:
- 代码中的问题链接了我的博客,有点受宠若惊,总结的很详细。
- 基于评分标准,我给本博客打分:11分。
- 得分情况如下:
- 正确使用Markdown语法(加1分)
- 模板中的要素齐全(加1分)
- 教材学习中的问题和解决过程, 四个问题加4分
- 代码调试中的问题和解决过程, 三个问题加3分
- 感想,体会不假大空的加1分
- 点评认真,能指出博客和代码中的问题的加1分
互评对象
-
本周结对学习情况
20172314方艺雯
20172323王禹涵 -
结对学习内容:堆和优先级队列
感悟
第十二章的优先队列与堆的内容并不是很难,和第十一章类似,都是在树的基础上添加附加条件,所以并不是很难,而且有很多示例代码可以学习,这样的话更减少困难。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 15/15 | |
| 第二周 | 703/703 | 1/2 | 20/35 | |
| 第三周 | 762/1465 | 1/3 | 20/55 | |
| 第四周 | 2073/3538 | 1/4 | 40/95 | |
| 第五周 | 981/4519 | 2/6 | 40/135 | |
| 第六周 | 1088/5607 | 2/8 | 50/185 | |
| 第七周 | 1203/6810 | 1/9 | 50/235 | |
| 第八周 | 2264/9074 | 2/11 | 50/285 |


