codeforce Hello 2018 913F sol

我们发现，一个大小为X的集合的答案和在里面的元素是无关的。那么我们用ans[n]表示大小为n时的答案。

我们考虑如何转移这个答案。 我们发现ans[0]=ans[1]=0;

我们考虑增量法，答案可以被拆成最后一个强连通分量和之前的那部分，我们给出以下转移式

 

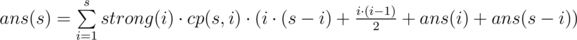
strong[i]表示一个大小为i的点集有strong[i]的期望成为一个强联通分量。cp[s,i]表示s个人里面有i个人输给了其他s-i个人。

那么我们发现strong[i]*cp[s,i]=在s个点的集合中，最后i个构成一个强连通分量的可能性。

我们考虑一张缩点以后的图，这是一张DAG，那么我们总有一个点出度为0，我们不妨让其为最后一个强连通分量，我们发现cp[s,i]*strong[i]正好是存在这样一个强连通分量的概率。

我们考虑怎么求cp：cp(s, i) = cp(s - 1, i)·(1 - p)ⁱ + cp(s - 1, i - 1)·p^s - i  

我们每次新加入一个点，有两种情况，这个点下标很大，对应cp(s - 1, i)·(1 - p)ⁱ    （因为他要全赢）

同理，这个下标小的时候，就是cp(s - 1, i - 1)·p^s - i  

那么我们考虑如何求strong[i].

我们分析发现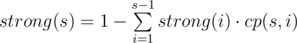，. ，我们枚举最后一个强连通分量的大小，将其期望减去，剩下的就是要求的答案。

那么我们就做完了。

#include<bits/stdc++.h>
#define LL long long
#define sight(c) ('0'<=c&&c<='9')
#define mo 998244353
#define N 2007
inline void read(int &x){
    static char c;
    for (c=getchar();!sight(c);c=getchar());
    for (x=0;sight(c);c=getchar()) x=x*10+c-48;
}
LL qsm(LL x,LL y){
    static LL anw;
    for (anw=1;y;y>>=1,x=x*x%mo) if (y&1) anw=anw*x%mo;
    return anw;
}
using namespace std;
LL p,cp[N][N],s[N],ans[N];
int a,b,n;
int main () {
//    freopen("f.in","r",stdin);
    read(n);
    read(a); read(b); p=a*qsm(b,mo-2)%mo;
    cp[0][0]=1;
    for (int i=0;i<n;i++) 
      for (int j=0;j<=i;j++)    
        (cp[i+1][j]+=qsm(p,j)*cp[i][j]%mo)%=mo,
        (cp[i+1][j+1]+=qsm((mo+1-p)%mo,i-j)*cp[i][j]%mo)%=mo;
    s[1]=1;
    for (int i=1;i<=n;i++,s[i]=1)
     for (int j=1;j<i;j++)
      s[i]=((s[i]-s[j]*cp[i][j]%mo)%mo+mo)%mo;
    for (int i=2;i<=n;i++)     {
        for (int j=1;j<i;j++)
         ans[i]=ans[i]+s[j]*cp[i][j]%mo*
         (((ans[j]+ans[i-j])%mo+(j-1)*j/2+j*(i-j))%mo)%mo,
         ans[i]=ans[i]%mo;
        ans[i]=(ans[i]+i*(i-1)/2*s[i])%mo;
        ans[i]=ans[i]*qsm((mo+1-s[i])%mo,mo-2)%mo;
    }
    printf("%lld\n",ans[n]); return 0;
    
}