后缀自动机
后缀自动机,是一种线性的字符串处理工具:
引用一下陈立杰的PPT
有限状态自动机的功能是识别字符串,令一个自动机A,若它能识别字符串S,就记为A(S)=True,否则A(S)=False。
自动机由五个部分组成,alpha:字符集,state:状态集合,init:初始状态,end:结束状态集合,trans:状态转移函数。
不妨令trans(s,ch)表示当前状态是s,在读入字符ch之后,所到达的状态。
如果trans(s,ch)这个转移不存在,为了方便,不妨设其为null,同时null只能转移到null。
null表示不存在的状态。
同时令trans(s,str)表示当前状态是s,在读入字符串str之后,所到达的状态
S为自动机的节点,那么我们可以这样定义S
struct S{ int c[26],fa,val;//26为字符集的大小,通常我们认为其为常数 }T[N];
那么自动机A能识别的字符串就是所有使得 trans(init,x) ⊂ end的字符串x。 令其为Reg(A)。
从状态s开始能识别的字符串,就是所有使得 trans(s,x) ⊂ end的字符串x。
令其为Reg(s)。
给定字符串S
S的后缀自动机suffix automaton(以后简记为SAM)是一个能够识别S的所有后缀的自动机。
即SAM(x) = True,当且仅当x是S的后缀
同时后面可以看出,后缀自动机也能用来识别S所有的子串。
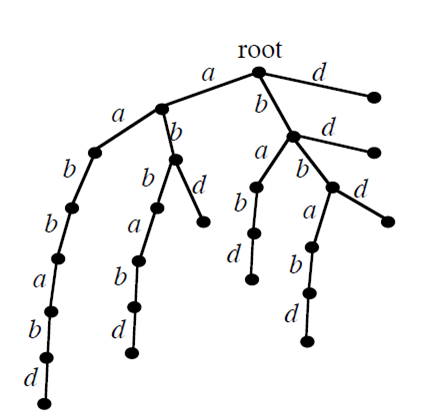
考虑字符串”aabbabd”
我们可以讲该字符串的所有后缀 插入一个Trie中,就像右图那样。 那么初始状态就是根,状态转移 函数就是这颗树的边,结 束状态 集合就是所有的叶子。
注意到这个结构对于长度为N
的串,会有O(𝑁^2)的节点。
那么,我们就要寻找最简状态的后缀自动机:
假如我们得到了这个最简状态后缀自动机SAM。
我们令ST(str)表示trans(init,str)。就是初始状态开始读入字符串str之后,能到达的状态。
令母串为S,它的后缀的集合为Suf,它的连续子串的集合为Fac。 从位置a开始的后缀为Suffix(a)。 S[l,r)表示S中[l,r)这个区间构成的子串。 下标从0开始。
对于一个字符串s,如果它不属于Fac,那么ST(s) = null。因为s后面加上任何字符串都不可能是S的后缀了,没有理由浪费空间。
同时如果字符串s属于Fac,那么ST(s) ≠ null。因为s既然是S的子串,就可以在后面加上一些字符使得其变成S的后缀。我们既然要识别所有的后缀,就不能放过这种 可能性。
我们不能对每个s∈Fac都新建一个状态,因为Fac的大小是O(𝑁2)的。
我们考虑ST(a)能识别哪些字符串,即Reg(ST(a))
字符串x能被自动机识别,当且仅当x∈Suf。
ST(a)能够识别字符串x,当且仅当ax∈Suf。因为我们已经读入了字符串a了。
也就是说ax是S的后缀。那么x也是S的后缀。Reg(ST(a))是一些后缀集合。
对于一个状态s,我们唯一关心的是Reg(s)。
说句人话,后缀自动机的核心是缩点,一颗后缀树上度为一的连续的点是没有必要单独存储的,我们可以将其缩成一个点表示一段区间,那么我们可以证明点的个数是不会超过2n-1个的。那么最简后缀自动机的节点数也是这样的。
我们假设这样一个节点a
如果a在S中的[l,r)位置出现,那么他就能识别S从r开始的后缀。
不妨令Right(a)=那么Reg(ST(a))就完全由Right(a)决定。
那么对于两个子串𝑎,𝑏∈𝐹𝑎𝑐如果Right(a) = Right(b),那么ST(a) = ST(b)。
所以一个状态s,由所有Right集合是Right(s)的字符串组成。
不妨令r∈𝑅𝑖𝑔𝑡(𝑠),那么只要给定子串的长度len,该子串就是S[r-len,r)。即给定Right集合后,再给出一个长度就可以确定子串了。
考虑对于一个Right集合,容易证明如果长度𝑙,𝑟合适,那么长度𝑙≤𝑚≤𝑟的m也一定合适。所以合适长度必然是一个区间。
不妨令s的区间是[Min(s),Max(s)]
我们考虑两个状态a,b。他们的Right集合分别为Ra,Rb。
假设Ra和Rb有交集,不妨设𝑟∈𝑅𝑎 ∩𝑅𝑏。
那么由于a和b表示的子串不会有交集,所以[Min(a),Max(a)]和[Min(b),Max(b)]也不会有交集。 不妨令Max(a)<Min(b)。那么a中所有长度都比b中短,由于都是由r往前,所以a中所有串都是b中所有串的后缀。因此a中某串出现的位置,b中某串也必然出现了。所以𝑅𝑎⊂𝑅𝑏。既Ra是Rb的真子集。
那么,任意两个串的Right集合,要么不相交,要么一个是另一个的真子集。
我们可以看出Right集合实际上构成了一个树形结构。不妨称其为Parent树。
在这个树中,叶子节点的个数只有N个,同时每内部个节点至少有2个孩子,容易证明树的大小必然是O(N)的。
令一个状态s,我们令fa=Parent(s)表示上面那个图中,它的父亲。 那么𝑅𝑖𝑔𝑡𝑓𝑎⊃𝑅𝑖𝑔𝑡𝑠,并且Right(fa)的大小是其中最小的。
考虑长度,s的范围是[Min(s),Max(s)],为什么长度Min(s)-1为什么不符合要求?可以发现肯定是因为出现的地方超出了Right(s)。同时随着长度的变小,出现的地方越来越多,那么Min(s)-1就必然属于fa的范围。那么
Max(fa) = Min(s)-1
我们已经证明了状态的个数是O(N)的,为了证明这是一个线性大小的结构,我们还需要证明边的大小是O(N)的。
如果trans(a,c) == null,我们就没有必要储存这条边,我们只需要储存有用的边。
不妨trans(a,c)=b的话,就看成有一条𝑎→𝑏的标号为c的边。
我们首先求出一个SAM的生成树(注意,跟之前提到的树形结构没有关系),以init为根。
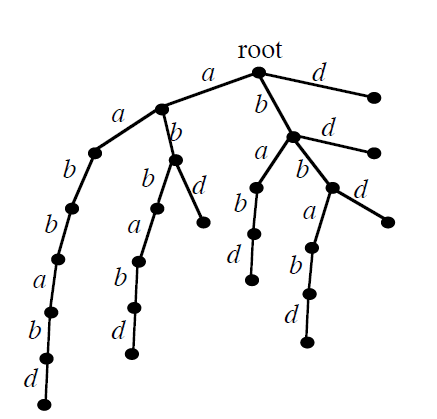
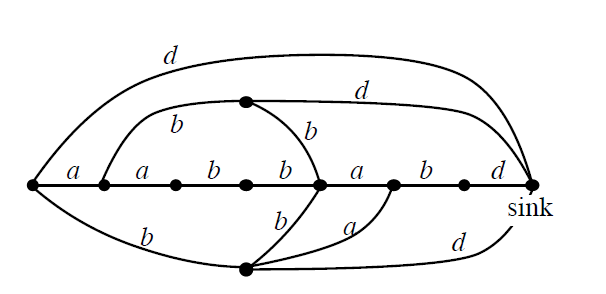
那么令状态数为M,,生成树中的边最多只有M-1条,接下来考虑非树边。对于一条非树边a→b标号为c。
我们构造:
生成树中从根到状态𝑎的路径+(a->b)+b到任意一个end状态。
可以发现这是一条从init到end状态的路径,由于这是一个识别所有后缀的后缀自动机,因此这必然是一个后缀。
那么一个非树边可以对应到多个后缀。我们对每个后缀,沿着自动机走,将其对应上经过的第一条非树边。
那么每个后缀最多对应一个非树边,同时一个非树边至少被一个后缀所对应,所以非树边的数量不会超过后缀的数量。
所以边的数量也不会超过O(N)
由于每个子串都必然包含在SAM的某个状态里。
那么一个字符串s是S的子串,当且仅当,ST(s)!=null
那么我们就可以用SAM来解决子串判定问题。
同时也可以求出这个子串的出现个数,就是所在状态Right集合的大小
在一个状态中直接保存Right集合会消耗过多的空间,我们可以发现状态的Right就是它Parent树中所有孩子Right集合的并集,进一步的话,就是Parent树中它所有后代中叶子节点的Right集合的并集。
那么如果按dfs序排列,一个状态的right集合就是一段连续的区间中的叶子节点的Right集合的并集,那么我们也就可以快速求出一个子串的所有出现位置了。
树的dfs序列:所有子树中节点组成一个区间。
我们的构造算法是Online的,也就是从左到右逐个添加字符串中的字符。依次构造SAM。
这个算法实现相比后缀树来说要简单很多,尽管可能不是非常好理解。
让我们先回顾一下性质
状态s,转移trans,初始状态init,结束状态集合end。
母串S,S的后缀自动机SAM(Suffix Automaton的缩写)。
Right(str)表示str在母串S中所有出现的结束位置集合。
一个状态s表示的所有子串Right集合相同,为Right(s)。
Parent(s)表示使得Right(s)是Right(x)的真子集,并且Right(x)的大小最小的状态x。
Parent函数可以表示一个树形结构。不妨叫它Parent树。
一个Right集合和一个长度定义了一个子串。
对于状态s,使得Right(s)合法的子串长度是一个区间,为| [Min(s),Max(s)]
Max(Parent(s)) = Min(s)-1。
SMA的状态数量和边的数量,都是O(N)的。
不妨令trans(s,ch)==null表示从s出发没有标号为ch的边,
考虑一个状态s,它的Right(s)=𝑟1,𝑟2,…,𝑟𝑛 ,假如有一条s→t标号为c的边,考虑t的Right集合,由于多了一个字符,s的Right集合中,只有S[𝑟𝑖]==c的符合要求。那么t的Right集合就是{𝑟𝑖+1|S[ri]==c}
那么如果s出发有标号为x的边,那么Parent(s)出发必然也有。
同时,对于令f=Parent(s),
Right(trans(s,c)) ⊆ Right(trans(f,c))。
有一个很显然的推论是Max(t)>Max(s)
我们每次添加一个字符,并且更新当前的SAM使得它成为包含这个新字符的SAM。
令当前字符串为T,新字符为x,令T的长度为L
SAM(T) →SAM(Tx)
那么我们新增加了一些子串,它们都是串Tx的后缀。
Tx的后缀,就是T的后缀后面添一个x
那么我们考虑所有表示T的后缀(也就是Right集合中包含L)的节点𝑣1,𝑣2,𝑣3,…。
由于必然存在一个Right(p)={L}的节点p(ST(T))。那么𝑣1,𝑣2,…,𝑣k由于Right集合都含有L,那么它们在Parent树中必然全是p的祖先。可以使用Parent函数得到他们。
同时我们添加一个字符x后,令np表示ST(Tx),则Right(np) ={L+1}
不妨让他们从后代到祖先排为𝑣1=𝑝,𝑣2,…,𝑣k=root。
考虑其中一个v的Right集合=𝑟1,𝑟2,…,𝑟𝑛=𝐿。
那么在它的后面添加一个新字符x的话,形成新的状态nv的话,只有S[𝑟𝑖] = x的𝑟𝑖那些是符合要求的。
同时在之前我们知道,如果从v出发没有标号为x的边(我们先不看𝑟𝑛),那v的Right集合内就没有满足这个要求的𝑟𝑖 。
那么由于𝑣1,𝑣2,𝑣3,… 的Right集合逐渐扩大,如果𝑣𝑖出发有标号为x的边,那么𝑣𝑖+1出发也肯定有。
对于出发没有标号为x的边的v,它的Right集合内只有𝑟𝑛是满足要求的,所以根据之前提到的转移的规则,让它连一条到np标号为x的边。
令𝑣𝑝为𝑣1,𝑣2,…,𝑣k中第一有标号为x的边的状态。
考虑𝑣𝑝的Right集合=𝑟1,𝑟2,…,𝑟𝑛 ,令trans(𝑣𝑝,x)=q
那么q的Right集合就是{𝑟𝑖+1},S[𝑟𝑖 ]=x的集合(注意到这是更新之前的情况,所以𝑟𝑛是不算的)。
注意到我们不一定能直接在q的Right集合中插入L+1。
那么我们新建一个节点nq,使Right(nq) = Right(q) ∩𝐿+1
同时可以看出Max(nq) = Max(𝑣𝑝)+1。
那么由于Right(q)是Right(nq)的真子集,所以Parent(q) = nq。
同时Parent(np) = nq。
并且容易证明Parent(nq) = Parent(q) (原来的)
接下来,如果新建了节点nq我们还得处理。
回忆: 𝑣1,𝑣2,…,𝑣k是所有Right集合包含{L}的节点按后代到祖先排序,其中𝑣𝑝是第一个有标号为x的边的祖先。x是这轮新加入的字符。
由于𝑣p,…,𝑣k都有标号为x的边,并且到达的点的Right集合,随着出发点Right集合的变大,也会变大,那么只有一段𝑣p,…,𝑣𝑒,通过标号为x的边,原来是到结点q的。 回忆:q=Trans(𝑣p,x)。
那么由于在这里q节点已经被替换成了nq,我们只要把𝑣p,…,𝑣𝑒的Trans(*,x)设为nq即可。
代码实现
inline int Sam(int x,int last){ int np=++tot; T[np].val=T[last].val+1; for(;last&&(!T[last].c[x]);last=T[last].fa) T[last].c[x]=np; if (!last) T[np].fa=1; else { int q=T[last].c[x]; if (T[last].val+1==T[q].val) T[np].fa=q; else { int nq=++tot; T[nq]=T[q]; T[nq].val=T[last].val+1; T[q].fa=T[np].fa=nq; for (;last&&T[last].c[x]==q;last=T[last].fa) T[last].c[x]=nq; } }return np; }
后附洛谷 【模板】后缀自动机的源代码:
//#pragma optimize("-O2") #include<bits/stdc++.h> #define N 3000003 #define max(a,b) ((a)>(b)?(a):(b)) #define min(a,b) ((a)<(b)?(a):(b)) using namespace std; struct S{ int c[26],fa,val; }T[N]; int tot=1,tmp,n,len,c[N],id[N],now,ti,x,last,siz[N]; long long ans; char ch[N]; inline int Sam(int x,int last){ int np=++tot; T[np].val=T[last].val+1; for(;last&&(!T[last].c[x]);last=T[last].fa) T[last].c[x]=np; if (!last) T[np].fa=1; else { int q=T[last].c[x]; if (T[last].val+1==T[q].val) T[np].fa=q; else { int nq=++tot; T[nq]=T[q]; T[nq].val=T[last].val+1; T[q].fa=T[np].fa=nq; for (;last&&T[last].c[x]==q;last=T[last].fa) T[last].c[x]=nq; } } siz[np]=1; return np; } int main () { freopen("a.in","r",stdin); scanf("%s",ch); len=strlen(ch);last=1; for (int i=0;i<len;i++) last=Sam(ch[i]-'a',last); for (int i=1;i<=tot;i++) c[T[i].val]++; for (int i=1;i<=len;i++) c[i]+=c[i-1]; for (int i=1;i<=tot;i++) id[c[T[i].val]--]=i; for (int i=tot;i;i--) { int p=id[i]; siz[T[p].fa]+=siz[p]; if (siz[p]>1) ans=max(ans,1ll*siz[p]*T[p].val); } printf("%lld\n",ans); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号