第2章--感知机

感知机（perceptron）是二类分类的线性分类模型。其输入为实例的特征（一个特征对应实数，多个特征对应向量）；输出为实例的类别，取+1和-1二值。感知机对应于输入空间中将实例划分为正负两类的分离超平面。

2.1 感知机模型

假设输入空间是$X \subseteq  R^{n} $，输出空间$\mathcal{Y} = \{+1, -1\}$。输入$x \in X$表示实例的特征，对应输入空间的一点。$y \in \mathcal{Y}$表示实例的类别。由输入空间到输出空间的如下函数：

\begin{align*}
f(x) = sign(w\cdot x + b)
\end{align*}

称为感知机。其中，$w \subseteq  R^{n} $叫做权重（weight），$b \in R$叫做偏置（bias）。sign是符号函数。即：

\begin{align*}
sign(x) = \left\{\begin{matrix} +1, \qquad x \geq 0
\\-1, \qquad x < 0
\end{matrix}\right.
\end{align*}

我们需要通过训练集的训练，求得合适的$w$和$b$。

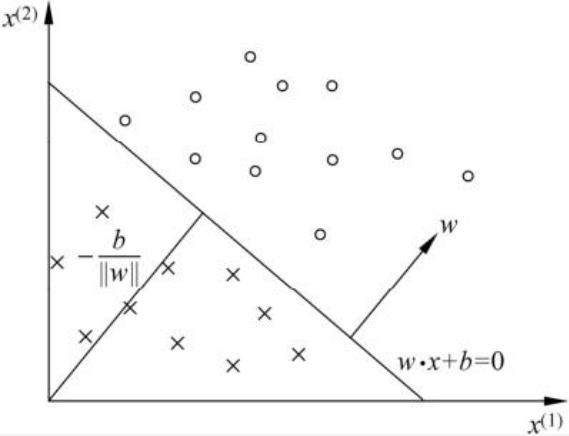
线性方程$w\cdot x + b = 0$对应输入空间$R^{n}$中的一个超平面$S$，其中w是超平面的发现，b是截距。该超平面将输入空间分为两部分，分别对应正样本和负样本。

已二维空间为例，输入空间$R^{n}$是一个平面，$S$是一条线，如下图所示：

2.2 损失函数及模型训练

容易想到把误分类点的个数作为损失函数。但这样的函数不是模型参数$w$、$b$的连续可导函数，不易优化。感知机采用的损失函数是误分类点到超平面的总距离。

首先写出$R^{n}$中的任一点$x_0$到超平面$w\cdot x + b = 0$的距离公式：

\begin{align*}
\frac{1}{\left \| w \right \|} \left | w \cdot x_0 + b \right |
\end{align*}

其中，$\left \| w \right \|$是$w$的$L_2$距离。

另外，对于误分类样本$(x_i, y_i)$有：

\begin{align*}
-y_i(w\cdot x_i + b ) > 0
\end{align*}

因此误分类点到超平面距离可写作：

\begin{align*}
-\frac{1}{\left \| w \right \|} y_0(w \cdot x_0 + b)
\end{align*}

不考虑$\frac{1}{\left \| w \right \|}$，或者始终对$w$向量做正规化（normalize），得到感知机的损失函数：

\begin{align*}
L(w, b) = -\sum_{x_i \in M} y_i(w\cdot x_i + b)
\end{align*}

其中，$M$是误分类样本点的集合。

求得偏导数：

\begin{align*}
& \frac{\partial L}{\partial w} = -\sum_{x_i \in M} y_ix_i \\
& \frac{\partial L}{\partial b} = -\sum_{x_i \in M} y_i \\
\end{align*}

其中，$x$、$w$的取值均可以是向量，$b$的取值是实数。

然后就可通过梯度下降（或者随机梯度下降，可参考梯度下降求解线性回归）对该损失函数求解。