ROC曲线的计算
1、ROC曲线简介
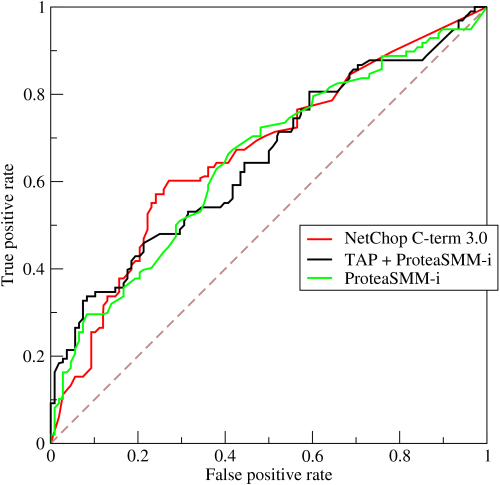
在评价分类模型时,会用到ROC(receiver operating characteristic)曲线。ROC曲线可用来评价二元分类器( binary classifier)的优劣,如下图:
假设我们的样本分为正(positive)、负(negative)两类,
- x轴false positive rate(FPR)表示:将负样本错误预测为正样本的比例。计算公式:负样本预测为正样本的数量 除以 负样本的总数。
- y轴true positive rate(TPR)表示:预测正确的正样本,在所有正样本中所占的比例,也就是正样本的召唤率。计算公式:预测正确的正样本数量 除以 正样本的总数。
考虑图中(0,0) (1,1) (0,1) (1,0) 四个点:
- (0,0)表示:FPR=0,TPR=0。没有负样本预测错误(也就是负样本全部预测正确),正样本全部预测错误。这说明把全部样本都预测为了负样本。
- (1,1)表示:FPR=1,TPR=1。负样本全部预测错误,正样本全部预测正确。这说明把全部样本都预测为了正样本。
- (0,1)表示:FPR=0,TPR=1。负样本全部预测正确,正样本全部预测正确。这个模型很完美。
- (1,0) 表示:FPR=1,TPR=0。负样本全部预测错误,正样本全部预测错误。这个模型太烂了。
也就是说,曲线越偏向于左上角,说明模型越好。但是上图中的三条曲线(对应三个模型)相互交叉,并不容易区分哪个模型更优,于是就引出了一个新的指标:
我们将曲线与x轴、直线x=1围成的面积,称作AUC(Area under the curve)。AUC位于0到1之间,取值越大说明模型越好。
2、ROC的计算
2.1、求解示例
首先看一个sklearn.metrics.roc_curve求解ROC的示例:
>>> import numpy as np >>> from sklearn import metrics >>> y = np.array([1, 1, 2, 2]) >>> scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2) >>> fpr array([ 0. , 0.5, 0.5, 1. ]) >>> tpr array([ 0.5, 0.5, 1. , 1. ]) >>> thresholds array([ 0.8 , 0.4 , 0.35, 0.1 ])
该示例有4个样本,参数说明如下:
- y:样本的真值
- pos_label=2:表明取值为2的样本是正样本。
- scores:预测出的某样本是正样本的概率。
- fpr、tpr:每个(fpr[i], tpr[i])都表示ROC曲线上的一个点,一共求解出了4个点。
- thresholds:求解(fpr[i], tpr[i])时使用的阈值。
2.2、求解步骤
可以看出,阈值thresholds就是对概率scores进行了排序(倒序)。不断改变阈值,得到ROC曲线上不同的点。步骤如下:
- threshold取0.8:也就是说预测概率大于等于0.8时,我们将样本预测为正样本。那么4个样本的预测结果为[1, 1, 1, 2]。负样本全部预测正确,正样本全部找到了。从而得到ROC曲线上一个点(0, 0.5)
- threshold取0.4:预测概率大于等于0.4时,认为是正样本。预测结果为[1, 2, 1, 2]。结果比上次糟糕,负样本一个预测错误,正样本一个没有找到,从而得到ROC上面的(0.5, 0.5)点。
- threshold取0.35:预测概率大于等于0.35时,认为是正样本。得到预测结果[1, 2, 2, 2]。负样本一个预测错误,正样本全部找出来了,从而得到(0.5, 1)
- threshold取0.1:预测大于等于0.1时,就认为是正样本。尽管召回率很高,但预测结果再次变差,把所有样本都预测为了正样本,从而得到(1, 1)点。