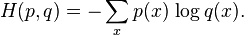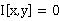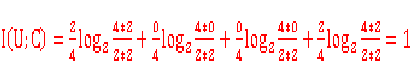信息论
http://www.cnblogs.com/rocketfan/archive/2010/09/24/1833839.html
惊讶度 相加关系 不相关 p(x,y)=p(x)p(y) 如果按信息量 不相关应该信息量累加 相加 所以 log
h(x) = -log(p(x))
信息平均而言 H(x) = -p(x)log(p(x))dx huffman 最优编码
推广到连续 高斯 对应 方差大 平缓 信息量高
条件信息量 H(Y|X) = -p(x,y)log(p(y|x))dxdy

H(X,Y)= H(X) + H(Y|X)

离散情况的例子

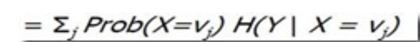

相对信息量 编码的时候不知道实际p(x) 用q(x)代替
B= -p(x)log(q(x))dx 那么得到的不是最优编码 值较大 多了一部分冗余信息
kl divergence
Kl(p,q) = B - H(x) >= 0 证明
表征了分布的相似性 如果=0 则分布相同
回到随机变量传输问题,假设传输中我们不知道具体
分布情况(unknown),我们用一个已知的分布
,来模拟它,那么在这种情况下如果我们利用
尽可能高效的编码,那么我们平均需要多少额外的信息量来描述x呢。这称为相对熵,或者kl divergence。
利用凸函数的不等式性质(也利用了离散求和推广到连续积分)可以证明
因此KL表征了两个分布之间的关系,a measure of dissimilariy of p and q表示两个分布不相同的程度
KL(p || q) != KL(q || p) 非对称
来自 <http://www.cnblogs.com/rocketfan/archive/2010/09/24/1833839.html>
交叉熵的概念
The cross entropy for the distributions  and
and  over a given set is defined as follows:
over a given set is defined as follows:
where  is the entropy of
is the entropy of  , and
, and 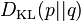 is the Kullback–Leibler divergence of
is the Kullback–Leibler divergence of  from
from  (also known as the relative entropy of p with respect to q — note the reversal of emphasis).
(also known as the relative entropy of p with respect to q — note the reversal of emphasis).
For discrete  and
and  this means
this means
相对信息量(relative ) 引出 互信息 (mutual)
Kl(p(x,y),p(x)p(y)) 用来表示 两个随机变量相关的程度 如果不相关是0 分值越大 相关性越高
I[x,y]
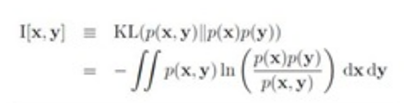
I[x,y] = H[x] - H[x|y] = H[y] -H[y|x] = H[x] +H[y] - H[x,y] 下面的关系图非常直观
即x,y无关,也即观测到y的情况下观测x的信息量等于直接观测到x的信息量(y不提供额外的信息帮助),
这种情况H[x]=H[x|y]
来自 <http://www.cnblogs.com/rocketfan/archive/2010/09/24/1833839.html>
http://baike.baidu.cn/view/1974678.htm
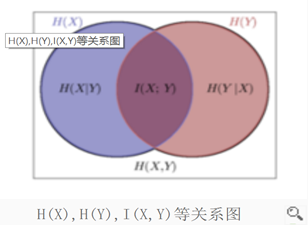
这个图很直观! 什么是互信息? x的信息量 - 知道y的情况下x剩下的信息量
Thus we can view the mutual information as the reduction in the uncertainty about x
by virtue of being told the value of y (or vice versa). From a Bayesian perspective,
we can view p( x ) as the prior distribution for x and p( x|y ) as the posterior distribu-
tion after we have observed new data y . The mutual information therefore represents
the reduction in uncertainty about x as a consequence of the new observation y .
互信息应用 文本分类中特征词的选取
度量一个词在文本的分布概率 与在某个类的分布概率 的 互信息
,使用互信息理论进行特征抽取是基于如下假设:在某个特定类别出现频率高,但在其他类别出现频率比较低的
词条与该类的互信息比较大。通常用互
信息作为特征词和类别之问的测度,如果特征词属于该类的话,它们的互信息量最大。
来自 <http://baike.baidu.cn/view/1974678.htm>

注意简单的例子 演示 特征词 也可能是负特征词
c++都出现在b类里面 那么对应c类的关系 互信息仍然为 1
case2:
个人认为上面log里面出现了0,可以平滑处理或者假定log里出现0值就是0,因为
n->0取极限的话nlogn=0也可以按照下面计算
I[C]=1 //两种状态均为0.5可能性
I[C|U]=0.5*H[C|U=et=1]+0.5*H[C|U=et=0]=0+0=0 //每个都是只有1个确定状态了
所以I(U;C)=H[C]-H[C|U]=1 //原文写错了
互信息 = IG 信息增益 所以两种公式等价 第二种 更直观的表示出了信息增益,第一种更直观的表示了相关性的程度。
第二种避免了 log里面0出现?
点互信息的话只考虑都出现 就是第一个部分 不会有负特征词 分数>0
注意上面 这种解释 其实就是 decision tree的概念 我们选取最大信息增益的特征 即表征识别类别最好的特征 先分裂
那显然 = 1 是最最好的特征 与类别的互信息最大(2个类0.5 0.5的时候)
信息增益Gain(S,A)定义
已经有了熵作为衡量训练样例集合纯度的标准,现在可以定义属性分类训练数据的效力的度量标准。这个标准被称为"信息增益(information gain)"。简单的说,一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低(或者说,样本按照某属性划分时造成熵减少的期望)。更精确地讲,一个属性A相对样例集合S的信息增益Gain(S,A)被定义为:

这里的Gain(S,A) 类比上面的 I(C,U) = H( C ) - H(C | U) 考虑离散情况的I(C|U) ==
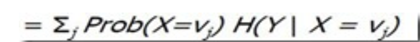
来自 <http://blog.csdn.net/v_july_v/article/details/7577684>
所以信息增益最大的选择 就是选择互信息最大的特征
互信息越高 增益越大 就是右侧值越小 也就是说在确定这个特征的值后 分类状态趋向明了 信息量大为减少 极端的就是 这个特征完全区分类别 比如具备这个特征就是A类 不具备 就不是A类 那么 右侧为0 也是上面特征词选择时候c++ 都在一个类别完全出现另一个类别完全不出现的情况

来自 <http://www.cnblogs.com/rocketfan/archive/2010/09/24/1833839.html> ID3 算法 贪婪 局部最优
另外一个例子
下面,举个例子,假定S是一套有关天气的训练样例,描述它的属性包括可能是具有Weak和Strong两个值的Wind。像前面一样,假定S包含14个样例,[9+,5-]。在这14个样例中,假定正例中的6个和反例中的2个有Wind =Weak,其他的有Wind=Strong。由于按照属性Wind分类14个样例得到的信息增益可以计算如下。

来自 <http://blog.csdn.net/v_july_v/article/details/7577684>
C4.5 算法
ID3算法 目标是信息增益 问题是会偏向取值多的属性
C4.5算法不再是通过信息增益来选择决策属性。一个可以选择的度量标准是增益比率gain ratio(Quinlan 1986)。增益比率度量是用前面的增益度量Gain(S,A)和分裂信息度量SplitInformation(S,A)来共同定义的,如下所示:
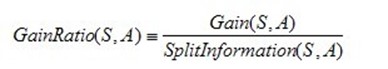
其中,分裂信息度量被定义为(分裂信息用来衡量属性分裂数据的广度和均匀):

来自 <http://blog.csdn.net/v_july_v/article/details/7577684>
相当于上面关系图的 I(x,y) / H(y)
使用增益比率代替增益来选择属性产生的一个实际问题是,当某个Si接近S(|Si|»|S|)时分母可能为0或非常小。如果某个属性对于S的所有样例有几乎同样的值,这时要么导致增益比率未定义,要么是增益比率非常大。为了避免选择这种属性,我们可以采用这样一些启发式规则,比如先计算每个属性的增益,然后仅对那些增益高过平均值的属性应用增益比率测试(Quinlan 1986)。
来自 <http://blog.csdn.net/v_july_v/article/details/7577684>
不同的思路 比如 特征词选取用互信息 再用bayes分类
也可以直接按照互信息词作为特征 decision tree 分类
语音语言处理 20.4 WSD word sense disambiguation
词的多义识别 selectional preference

看上去也是类似信息检索里面特征选取的那个例子 互信息表征类别偏好
但是它直接度量的不是才c, v的相关性(mutual info)而是 直接kl 对比 p( c ) p(c|v)的相似性
p(c,v)log( p(c,v) / p( c )p(v) )和 上面的差别 只有前面的 p(c|v)( p(c,v) / p( c )p(v) )
差一个p(v)
看下面给的例子 分值 与互信息不同 有负值 但是 kl >= 0的 Resnik重定义的那个A(v, c) TODO 实验一下
但是也不能有负数值啊。。。。


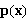



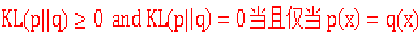
![H(p, q) = \operatorname{E}_p[-\log q] = H(p) + D_{\mathrm{KL}}(p \| q),\!](http://upload.wikimedia.org/math/f/4/a/f4ab2081ce7d74c25a097e1df32f77b2.png)