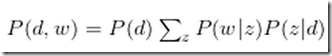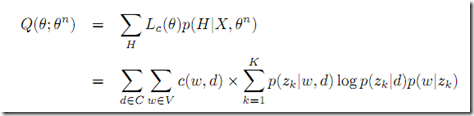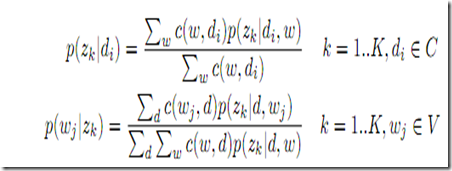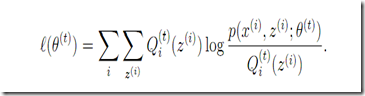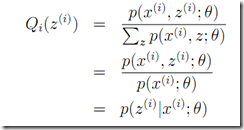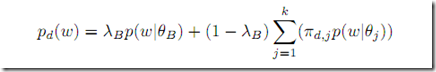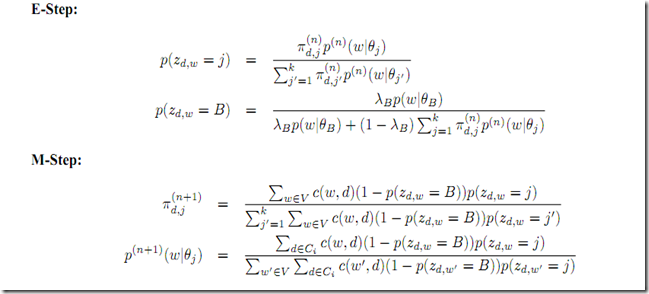PLSA中的EM算法
主要记录下几个文章博客内容
A Note on EM Algorithm for Probabilistic Latent SemanticAnalysis(翟成祥的NOTE)
A Note on EM Algorithm and PLSA(一个中文比较好的总结 by Xinyan Lu)
注意这两个是一个思路
Probabilistic Latent Semantic Analysis (原论文)
原论文是另一个思路
Notes on Probabilistic Latent Semantic Analysis (PLSA)(这个里面对比了两种不同思路,原论文与翟成祥NOTE,Xinyan Lu中文总结 分布对应这两种思路)
先看第一种思路,这个更好理解一点
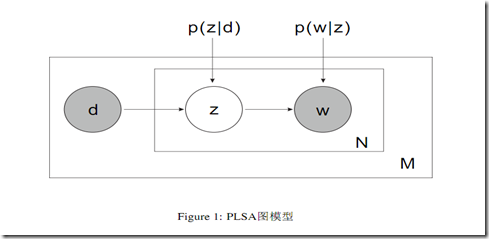
典型的EM算法 hidden/latent variable 是主题Z,p(d)对于我们的计算可忽略,最后面那个博客的总结证明更完整。
![]() 类似前面的混合高斯模型,这里实际Estep要估算的就是对应d,w 情况下Z的概率
类似前面的混合高斯模型,这里实际Estep要估算的就是对应d,w 情况下Z的概率
 Estep 对比前面高斯模型
Estep 对比前面高斯模型![]() 具体一个观察点情况下对应到隐藏分类的概率
具体一个观察点情况下对应到隐藏分类的概率
解释下 sum_z(p(z|d)p(w|z))= p(w|d) p(d)p(w|d)p(z|d,w) = p(d,w,z) => p(w|d)p(z|d,w) = p(d,w,z)/p(d) = p(w,z|d)=p(z|d)p(w|z)
=> p(z|w,d) = p(z|d)(pw|z) / p(w|d)
对比NG的课件
如果我们考虑背景噪音,翟成祥的NOTE更进一步给出了在这个基础上稍微复杂一点的MODLE和结果
第二种思路
TODO