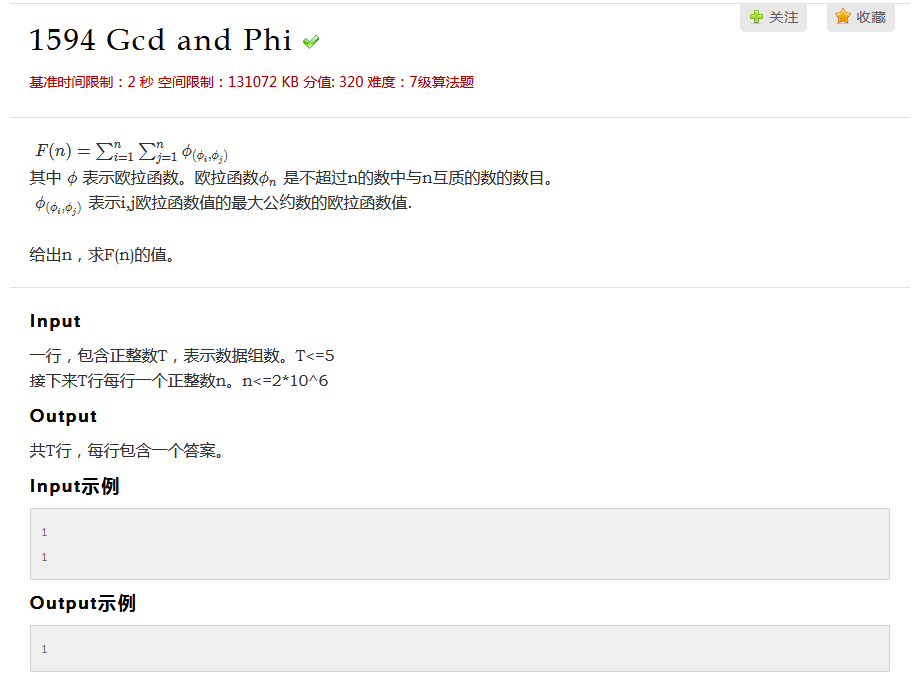
【莫比乌斯反演】51nod1594 Gcd and Phi

题解

 

 

显然可以O（nlogn）计算

 代码

 

//by 减维
#include<set>
#include<map>
#include<queue>
#include<ctime>
#include<cmath>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define il inline
#define rg register
#define db double
#define mpr make_pair
#define maxn 2000005
#define inf (1<<30)
#define eps 1e-8
#define pi 3.1415926535897932384626L
using namespace std;

inline int read()
{
    int ret=0;bool fla=0;char ch=getchar();
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    if(ch=='-'){fla=1;ch=getchar();}
    while(ch>='0'&&ch<='9'){ret=ret*10+ch-'0';ch=getchar();}
    return fla?-ret:ret;
}

int t,n,num,mu[maxn],pri[maxn],phi[maxn];
ll cnt[maxn],sum[maxn];
bool pd[maxn];

void pre()
{
    phi[1]=1;mu[1]=1;
    for(int i=2;i<=maxn-5;i++)
    {
        if(!pd[i]) pri[++num]=i,phi[i]=i-1,mu[i]=-1;
        for(int j=1;j<=num&&i*pri[j]<=maxn-5;++j)
        {
            pd[i*pri[j]]=1;
            if(i%pri[j]==0)
            {
                phi[i*pri[j]]=phi[i]*pri[j];
                break ;
            }
            phi[i*pri[j]]=phi[i]*phi[pri[j]];
            mu[i*pri[j]]=-mu[i];
        }
    }
}

il ll gcd(ll x,ll y){return y==0?x:gcd(y,x%y);}

ll solve(int x)
{
    memset(cnt,0,sizeof cnt);
    memset(sum,0,sizeof sum);
    for(int i=1;i<=x;++i) cnt[phi[i]]++;
    for(int i=1;i<=x;++i)
        for(int j=1;i*j<=x;++j) sum[i]+=cnt[i*j];
    ll ret=0;
    for(int d=1;d<=x;++d)
        if(mu[d])
            for(int dd=1;dd*d<=x;++dd)
                ret+=phi[dd]*mu[d]*sum[d*dd]*sum[d*dd];
    return ret;
}

int main()
{
    t=read();
    pre();
    while(t--)
    {
        n=read();
        printf("%lld\n",solve(n));
    }
    return 0;
}